

Up: Search for non-helical disc
Appendix D: Coulomb-gauged helicity flux
In the 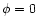 gauge we have
gauge we have
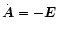 .
In that gauge,
the evolution of the magnetic helicity density is given by
.
In that gauge,
the evolution of the magnetic helicity density is given by
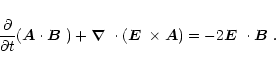 |
(D.1) |
Note that the term on the right hand side of this equation is
gauge-invariant, but the terms on the left hand side are not.
In the Coulomb gauge we have
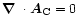 ,
where
,
where
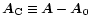 .
In order to maintain
.
In order to maintain
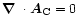 for all times, we have to add the term
for all times, we have to add the term
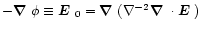 to the
right hand side of the uncurled induction equation,
to the
right hand side of the uncurled induction equation,
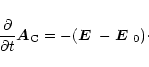 |
(D.2) |
In this gauge the evolution equation for the helicity density becomes
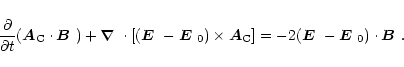 |
(D.3) |
Unlike Eq. (D.1), the right hand side of Eq. (D.3)
is gauge dependent
owing to the extra term
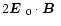 .
However, because of
.
However, because of
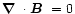 ,
we can write this as the divergence of another contribution to the
helicity flux density,
,
we can write this as the divergence of another contribution to the
helicity flux density,
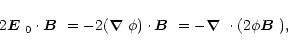 |
(D.4) |
which should be included in the expression for the Coulomb gauged
helicity flux density,
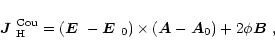 |
(D.5) |
so Eq. (D.3) becomes
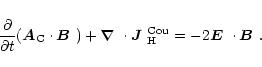 |
(D.6) |
Now the right hand sides of Eqs. (D.1) and (D.6)
agree and are gauge-invariant. Note, however, that
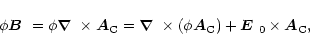 |
(D.7) |
so Eq. (D.5) can also be written as
![\begin{displaymath}\mbox{\boldmath$J$ } {}_{\rm H}^{\rm Cou}=
(\mbox{\boldmath$E...
...+\mbox{\boldmath$\nabla$ } {}\times[2\phi(\vec{A}-\vec{A}_0)],
\end{displaymath}](/articles/aa/full/2001/46/aah2980/img293.gif) |
(D.8) |
which is identical to Eq. (11).


Up: Search for non-helical disc
Copyright ESO 2001
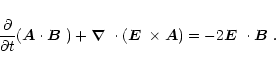
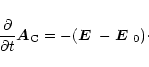
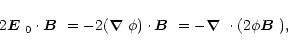
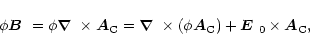
![\begin{displaymath}\mbox{\boldmath$J$ } {}_{\rm H}^{\rm Cou}=
(\mbox{\boldmath$E...
...+\mbox{\boldmath$\nabla$ } {}\times[2\phi(\vec{A}-\vec{A}_0)],
\end{displaymath}](/articles/aa/full/2001/46/aah2980/img293.gif)