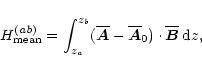 |
(B.1) |
Similar to Eq. (A.2), we can now derive an evolution equation for
![]() .
The
flux term is then like in Eq. (A.2), but with
.
The
flux term is then like in Eq. (A.2), but with
![]() being replaced by
being replaced by
![]() .
The magnetic helicity flux out of an individual sub-domain is then
.
The magnetic helicity flux out of an individual sub-domain is then
![]() ,
where
,
where
Copyright ESO 2001