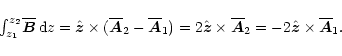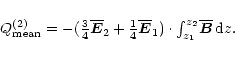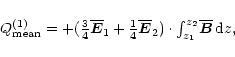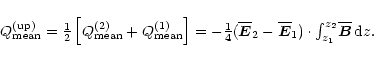Up: Search for non-helical disc
Appendix A: A gauge in which magnetic helicity and magnetic helicity flux are
automatically gauge invariant
The purpose of this appendix is to show that there is a particular gauge
for the vector potential of the one-dimensional mean field such that
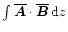 is automatically
gauge invariant. This allows us then to define a local helicity
flux such that its integral over a closed surface (top and bottom of a
slab) equals the gauge invariant integrated helicity flux of BD2001.
is automatically
gauge invariant. This allows us then to define a local helicity
flux such that its integral over a closed surface (top and bottom of a
slab) equals the gauge invariant integrated helicity flux of BD2001.
The evolution equation of the mean (one-dimensional)
magnetic vector potential is
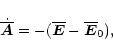 |
(A.1) |
where
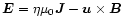 is the electric
field,
is the electric
field,
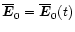 is an integration
constant, and
is an integration
constant, and
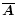 and
and
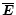 depend only on z and t. From Eq. (A.1) follows the evolution equation for
the magnetic helicity density,
depend only on z and t. From Eq. (A.1) follows the evolution equation for
the magnetic helicity density,
![\begin{displaymath}{\partial\over\partial t}({\overline{\vec{A}}}\cdot{\overline...
...rline{\vec{A}}}]
=-2\overline{\vec{E}}\cdot\overline{\vec{B}}.
\end{displaymath}](/articles/aa/full/2001/46/aah2980/img251.gif) |
(A.2) |
In BD2001 the gauge independent magnetic helicity
of the mean field was found to be
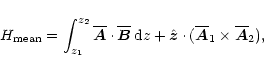 |
(A.3) |
where
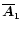 and
and
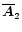 are the values
of
are the values
of
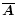 at z=z1 and z2, respectively. At the initial
time one can always subtract a constant from
at z=z1 and z2, respectively. At the initial
time one can always subtract a constant from
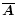 such that
the second term vanishes. This constant turns out to be the average
of
such that
the second term vanishes. This constant turns out to be the average
of
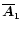 and
and
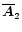 ,
so we replace initially
,
so we replace initially
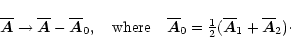 |
(A.4) |
Next we choose
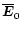 such that
such that
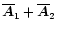 remains zero at all later
times. This yields
remains zero at all later
times. This yields
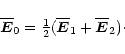 |
(A.5) |
We can then express the two integrated fluxes on z2 as
![\begin{displaymath}Q_{\rm mean}^{(2)}=\hat{\vec{z}}\cdot[
(\overline{\vec{E}}_2+...
...over2}}\overline{\vec{E}}_1)\times{\overline{\vec{A}}}_2]\cdot
\end{displaymath}](/articles/aa/full/2001/46/aah2980/img259.gif) |
(A.6) |
Using the fact that
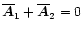 we
can write
we
can write
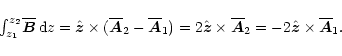 |
(A.7) |
This allows us to express
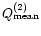 as
as
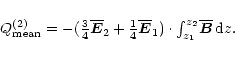 |
(A.8) |
At z=z1 we count the flux as negative when helicity leaves the domain
in the downward direction, so
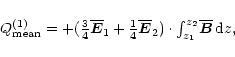 |
(A.9) |
with
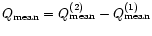 being the
gauge invariant magnetic helicity flux of BD2001.
The average upward flux of mean magnetic helicity on the two boundaries
is
being the
gauge invariant magnetic helicity flux of BD2001.
The average upward flux of mean magnetic helicity on the two boundaries
is
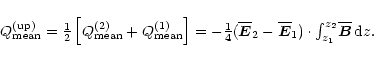 |
(A.10) |


Up: Search for non-helical disc
Copyright ESO 2001
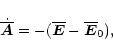
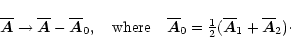
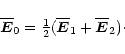
![\begin{displaymath}Q_{\rm mean}^{(2)}=\hat{\vec{z}}\cdot[
(\overline{\vec{E}}_2+...
...over2}}\overline{\vec{E}}_1)\times{\overline{\vec{A}}}_2]\cdot
\end{displaymath}](/articles/aa/full/2001/46/aah2980/img259.gif)