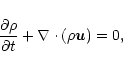 |
(1) |
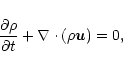 |
(1) |
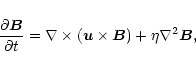 |
(3) |
In most of the models we apply closed boundary conditions for the
flow on the z-boundaries, with the magnetic field penetrating
the boundaries at right angles. One of the models (Model IX; see below) uses
open boundaries in the z-direction. The inner radial boundary is
open in all models; the mass flux is monitored on the inner boundary
and fed back into the domain on the
outer radial boundary with either a homogeneous or a Gaussian
infall pattern for the density.
The maximum infall velocity is constant in time and over zand is either 10-2 or 10-3 of the sound speed. The
![]() -direction has periodic boundaries.
-direction has periodic boundaries.
The initial configuration contains a relaxed disk with
a slow outflow on the inner boundary due to numerical viscosity. The
density scale height varies between
![]() and
0.66 between the radii r=4 and 6. In the absence of magnetic fields
the system is hydrodynamically stable; this
was verified numerically for up to 30 orbits
without producing any visible changes at the end of the simulation. The magnetic
field imposed to this configuration is merely a vertical Bz field
with zero net flux through the vertical surfaces.
and
0.66 between the radii r=4 and 6. In the absence of magnetic fields
the system is hydrodynamically stable; this
was verified numerically for up to 30 orbits
without producing any visible changes at the end of the simulation. The magnetic
field imposed to this configuration is merely a vertical Bz field
with zero net flux through the vertical surfaces.
Table 1 summarizes the global runs used for this
analysis. The same numbering of the models as in
Arlt & Rüdiger (2001) is used. Two of the simulations are new on
this list: Model Va is a repetition of the configuration of
Model V, but with an initial magnetic field of mixed
parity. The parity of the Bz field was zero at the beginning
as was the parity of the emerging ![]() field. All other models
start with an initial field parity of -1 (antisymmetry). Model IX
is similar to Model V, but uses outflow boundary conditions
for the vertical direction instead of closed boundaries.
In Table 1 the magnetic diffusivity
field. All other models
start with an initial field parity of -1 (antisymmetry). Model IX
is similar to Model V, but uses outflow boundary conditions
for the vertical direction instead of closed boundaries.
In Table 1 the magnetic diffusivity ![]() is also given
for all runs. Since the considerations presented here were
made after the actual production runs had been performed, only
a limited number of fully three-dimensional snapshots were
available, which is the reason for a relatively coarse sampling.
is also given
for all runs. Since the considerations presented here were
made after the actual production runs had been performed, only
a limited number of fully three-dimensional snapshots were
available, which is the reason for a relatively coarse sampling.
| Run | Grid (z, r, |
Radial boundary condition | r-range |
|
|
Init. parity | |
| II |
|
homogeneous accretion
|
4.0-6.0 | 0.159 | 14.7 | antisym. | 0.001 |
| III |
|
homogeneous accretion
|
4.0-6.0 | 0.159 | 9.7 | antisym. | 0.001 |
| VIII |
|
homogeneous accretion
|
3.0-7.0 | 0.103 | 22.4 | antisym. | 0.001 |
| V |
|
Gaussian accretion
|
4.0-6.0 | 0.159 | 18.4 | antisym. | 0.01 |
| Va |
|
Gaussian accretion
|
4.0-6.0 | 0.159 | 12.4 | mixed | 0.01 |
| VI |
|
Gaussian accretion
|
4.0-6.0 | 0.159 | 16.1 | antisym. | 0.01 |
| IX |
|
Gaussian accretion
|
4.0-6.0 | 0.159 | 16.9 | antisym. | 0.01 |
In the theory of VC2001 large scale magnetic field generation is possible
when there is a finite value of the correlation
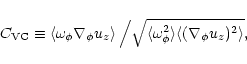 |
(4) |
A scatter plot of
![]() versus
versus
![]() is shown in
Fig. 2 for the data of a snapshot from Model V,
which has the largest (negative) correlation.
The plot contains points in the
is shown in
Fig. 2 for the data of a snapshot from Model V,
which has the largest (negative) correlation.
The plot contains points in the ![]() plane at r=5which is in the middle of the computational domain.
The plot looks rather noisy, but one sees nevertheless a slight negative
correlation.
plane at r=5which is in the middle of the computational domain.
The plot looks rather noisy, but one sees nevertheless a slight negative
correlation.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{h2980f1.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg81.gif) |
Figure 1:
Correlation of
|
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{h2980f2.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg82.gif) |
Figure 2:
Scatter plot of
|
We first discuss the overall field structure. Horizontal slices of the field at z=-0.39are shown for Models VIII (less resistive) and V (more resistive) in Figs. 3 and 4, respectively. The former figure exhibits a spiral pattern whilst the latter is rather dominated by intermediate scale structures or eddies, which is probably directly a consequence of the larger magnetic diffusivity in that case.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{h2980f3.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg83.gif) |
Figure 3: Projection of magnetic field vectors in a horizontal slice at z=-0.39of Model VIII after 19.9 orbits. |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{h2980f4.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg84.gif) |
Figure 4: Projection of magnetic field vectors in a horizontal slice at z=-0.39of Model V after 17.6 orbits. |
Next we derive a number of averaged quantities from the simulations.
Throughout this section we denote azimuthal averages by an overbar, e.g.
![]() .
In Fig. 5 are shown
the energies contained in the large scale field,
.
In Fig. 5 are shown
the energies contained in the large scale field,
![]() ,
and the
energies of the remaining fluctuations,
,
and the
energies of the remaining fluctuations,
![]() ,
where
,
where
![]() .
Like in
Fig. 1, the temporal evolution behaviours separate
into the same two groups: the low-
.
Like in
Fig. 1, the temporal evolution behaviours separate
into the same two groups: the low-![]() (less resistive) runs
which show significant energies in the
large scale field, and models with larger
(less resistive) runs
which show significant energies in the
large scale field, and models with larger ![]() that are more resistive,
but better able to generate
fluctuation energies of at least 50% of the large scale energy.
We note that there is one model (Model IX, not shown) where at the end the
energy of magnetic fluctuations exceeds the large scale magnetic energy.
The fact that the energy of the mean field is typically larger than
that of the fluctuating field is somewhat surprising. A possible reason
could be that the memory of the initial mean field has not yet been lost.
It is also possible, however, that it is because of the global geometry
and the shear that a strong large scale field is more easily established
when the magnetic Reynolds number is large.
that are more resistive,
but better able to generate
fluctuation energies of at least 50% of the large scale energy.
We note that there is one model (Model IX, not shown) where at the end the
energy of magnetic fluctuations exceeds the large scale magnetic energy.
The fact that the energy of the mean field is typically larger than
that of the fluctuating field is somewhat surprising. A possible reason
could be that the memory of the initial mean field has not yet been lost.
It is also possible, however, that it is because of the global geometry
and the shear that a strong large scale field is more easily established
when the magnetic Reynolds number is large.
Another distinction between the two groups of runs is given
by the magnetic Taylor microscale,
![]() ,
which we define
here via
,
which we define
here via
![]() .
In Fig. 6 we show the value of
.
In Fig. 6 we show the value of
![]() for the same four models as in Fig. 1.
The quantity
for the same four models as in Fig. 1.
The quantity
![]() characterized the typical thickness
of flux structures. Its significance is that in runs with dynamo action
characterized the typical thickness
of flux structures. Its significance is that in runs with dynamo action
![]() tends to increase with time until it reaches saturation
(e.g. Brandenburg et al. 1996). Conversely, when the field is amplified just
by field compression the value of
tends to increase with time until it reaches saturation
(e.g. Brandenburg et al. 1996). Conversely, when the field is amplified just
by field compression the value of
![]() decreases somewhat
with time. This is what happened in the more resistive runs (
decreases somewhat
with time. This is what happened in the more resistive runs (![]() ).
These were actually the runs that did show evidence for a finite
Vishniac-Cho correlation. In contrast, the less resistive runs
(
).
These were actually the runs that did show evidence for a finite
Vishniac-Cho correlation. In contrast, the less resistive runs
(
![]() )
do not show any such trend.
)
do not show any such trend.
A useful quantity for assessing the importance of helicity in the
large scale field is to look at the nondimensional quantity
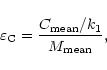 |
(5) |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{h2980f6.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg99.gif) |
Figure 6:
Comparison of the magnetic Taylor microscale
|
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{h2980f7.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg100.gif) |
Figure 7: Evolution of the nondimensional large-scale current helicity parameter (upper disc plane) for Models II and III (left), as well as Models V and Va (right). |
We now discuss the sign of
![]() .
In BD2001 the sign of the
kinetic helicity was positive, and so was the sign of the small
scale current helicity. The sign of the large scale current helicity
is typically opposite, i.e. negative in that case. In the present case,
where we consider the upper disc plane, the kinetic helicity is negative,
so we would expect a positive value of
.
In BD2001 the sign of the
kinetic helicity was positive, and so was the sign of the small
scale current helicity. The sign of the large scale current helicity
is typically opposite, i.e. negative in that case. In the present case,
where we consider the upper disc plane, the kinetic helicity is negative,
so we would expect a positive value of
![]() ,
which is not what
we find (except for one of the more resistive cases, Model Va). However,
the unusual sign of
,
which is not what
we find (except for one of the more resistive cases, Model Va). However,
the unusual sign of
![]() is
primarily related to an unusual sign of the effective
is
primarily related to an unusual sign of the effective ![]() found
in the present simulations.
This is because in the steady state the energy-generating effect,
found
in the present simulations.
This is because in the steady state the energy-generating effect,
![]() ,
must balance turbulent diffusion,
,
must balance turbulent diffusion,
![]() .
Therefore the sign of
.
Therefore the sign of ![]() must coincide
with the sign of
must coincide
with the sign of
![]() .
In discs, however, the sign of
.
In discs, however, the sign of ![]() is negative (in the upper disc plane),
so
is negative (in the upper disc plane),
so
![]() must also be negative, and
hence
must also be negative, and
hence
![]() is negative, as observed. The perhaps most
convincing explanation for the negative
is negative, as observed. The perhaps most
convincing explanation for the negative ![]() is that intense parts of
a flux tube contract (to maintain pressure balance along field lines),
but are also most
buoyant. If this contraction is stronger than the expansion associated
with the rise into a less dense medium,
is that intense parts of
a flux tube contract (to maintain pressure balance along field lines),
but are also most
buoyant. If this contraction is stronger than the expansion associated
with the rise into a less dense medium, ![]() will be negative
(Brandenburg 1998, see also Rüdiger & Pipin 2000).
will be negative
(Brandenburg 1998, see also Rüdiger & Pipin 2000).
We shall now return to the question of whether there is any evidence for the presence of a dynamo effect as envisaged by VC2001. We therefore need to look at the possibility of magnetic helicity fluxes through the domain.
| Run |
|
|
|
|
|
slope |
|
||
| North | South | North | South |
|
|||||
| II | 3.7 |
|
|
|
|
|
+0.00006 | -0.0024 | -0.012 |
| III | 7.5 |
|
|
|
|
|
+0.00007 | -0.0005 | +0.003 |
| VIII | 7.6 |
|
|
|
|
|
+0.00029 | -0.0018 | -0.005 |
| V | 3.8 |
|
|
|
|
|
-0.00013 | -0.0086 | -0.050 |
| Va | 5.3 |
|
|
|
|
|
-0.00038 | -0.0096 | -0.086 |
| VI | 4.0 |
|
|
|
|
|
-0.00157 |
|
-0.060 |
| IX | 2.9 |
|
|
|
|
|
+0.00007 | -0.0053 | -0.047 |
In VC2001 it was argued that, although the overall magnetic helicity is
small, there could still be a significant (spatially constant) flux
of magnetic helicity vertically through the domain. The numerical procedures
for evaluating gauge invariant magnetic helicity and magnetic helicity
flux in cylindrical geometry with open boundaries in the r and zdirections are not yet available. However, for the present purpose most important
is the contribution from the large scales. If we adopt horizontal averages
(over r and ![]() ), the mean fields are one-dimensional and the mean
magnetic vector potential can be obtained simply by integration. The
corresponding magnetic helicity and magnetic helicity fluxes of the
mean field can then be calculated quite easily (see the appendix of BD2001). In
Fig. 8 we plot, for the four models, the magnetic helicity
flux,
), the mean fields are one-dimensional and the mean
magnetic vector potential can be obtained simply by integration. The
corresponding magnetic helicity and magnetic helicity fluxes of the
mean field can then be calculated quite easily (see the appendix of BD2001). In
Fig. 8 we plot, for the four models, the magnetic helicity
flux,
![]() ,
out of the domain through the two
boundaries at z=z1 and z2. Here,
,
out of the domain through the two
boundaries at z=z1 and z2. Here,
![]() and
and
![]() denote the upward helicity fluxes at z=z1and z2, respectively; see Appendix A.
denote the upward helicity fluxes at z=z1and z2, respectively; see Appendix A.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2980f8.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg148.gif) |
Figure 8:
Estimates of the magnetic helicity flux
|
The mean outward flux, expressed in "dynamical'' units,
![]() ,
is small (
,
is small (
![]() ). A small outward flux was also
found in the case of helical turbulence (BD2001). Furthermore,
the signs tend to be different in the cases where
). A small outward flux was also
found in the case of helical turbulence (BD2001). Furthermore,
the signs tend to be different in the cases where ![]() is
small (
is
small (
![]() for
for
![]() )
and where
it is larger (
)
and where
it is larger (
![]() for
for
![]() ). It is doubtful
that this result indicates any significant departure from zero,
because the magnetic helicity on the two sides about the midplane of
the disc are expected to be different. Thus, equal losses or gains on
the two surfaces (z=z1 and z2) should result in zero net magnetic
helicity flux. It is therefore now necessary to determine the mean
upward fluxes of magnetic helicity on the two sides,
). It is doubtful
that this result indicates any significant departure from zero,
because the magnetic helicity on the two sides about the midplane of
the disc are expected to be different. Thus, equal losses or gains on
the two surfaces (z=z1 and z2) should result in zero net magnetic
helicity flux. It is therefore now necessary to determine the mean
upward fluxes of magnetic helicity on the two sides,
![]() and
and
![]() .
Its average is denoted by
.
Its average is denoted by
![]() .
If there is indeed a systematic upwards flux through the two boundaries,
this quantity should be finite and positive. As expected,
this quantity turns out to be small.
In order to check whether this is the result of some cancellation,
we need to consider the magnetic helicity fluxes in smaller sub-volumes.
.
If there is indeed a systematic upwards flux through the two boundaries,
this quantity should be finite and positive. As expected,
this quantity turns out to be small.
In order to check whether this is the result of some cancellation,
we need to consider the magnetic helicity fluxes in smaller sub-volumes.
A difficulty associated with calculating magnetic helicity and magnetic helicity fluxes separately in two sub-volumes (e.g., above and below the midplane) is that we want to make sure that the sum of the two is equal to the total magnetic helicity calculated earlier. This will be the case provided the magnetic helicity in each sub-domain is calculated using the same gauge that also made the helicity of the full domain gauge invariant. This then also allows one to calculate the integrated magnetic helicity fluxes out of each sub-domain. The corresponding formulae are given in Appendix B.
It turns out that the helicity fluxes out of each sub-volume are
actually large but of opposite sign. This means that there is actually
a large magnetic helicity flux through the midplane, but not through
the upper and lower boundaries. Having fixed the gauge such that
![]() is equal to
the helicity of BD2001 for the full domain, we can also calculate
the local magnetic helicity fluxes. We denote these by
is equal to
the helicity of BD2001 for the full domain, we can also calculate
the local magnetic helicity fluxes. We denote these by
![]() (if evaluated at the midplane), or by
(if evaluated at the midplane), or by
![]() (if calculated for all values of z).
In Fig. 9 we plot
(if calculated for all values of z).
In Fig. 9 we plot
![]() and
compare with the averaged boundary fluxes
and
compare with the averaged boundary fluxes
![]() .
It turns out that
.
It turns out that
![]() is indeed mostly positive,
as predicted by VC2001, but this flux is not sustained all the way
to the boundaries:
is indeed mostly positive,
as predicted by VC2001, but this flux is not sustained all the way
to the boundaries:
![]() is virtually zero by
comparison. An exception is Run Va, where
is virtually zero by
comparison. An exception is Run Va, where
![]() shows large variations about zero and
shows large variations about zero and
![]() begins
to deviate systematically from zero. (We recall that this is the run
where the initial field had mixed parity.)
begins
to deviate systematically from zero. (We recall that this is the run
where the initial field had mixed parity.)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{h2980f9.ps}
\end{figure}](/articles/aa/full/2001/46/aah2980/Timg158.gif) |
Figure 9:
Estimates of the integrated magnetic helicity fluxes
at the midplane,
|
In order to see whether the magnetic helicity flux at the midplane is typical of the entire interior of the simulation domain, we plot in Fig. 10 the vertical distribution of the magnetic helicity flux, which was derived from horizontal averages of field and flow and then averaged in time (again excluding the first 2 to 4 orbits). Figure 10 shows that a positive (i.e. upwards) flux of magnetic helicity is indeed typical of the interior of the entire domain, and that it vanishes only near the boundaries. Thus the boundaries seem to play an important role, which may of course be unrealistic. We note, however, even Model IX with open boundaries does show a rapid drop of magnetic helicity flux near the z-boundaries. Clearly, an abrupt change of this flux implies generation and destruction of magnetic helicity near the vertical boundaries.
To summarize the global disc simulations, the correlation
anticipated by VC2001 is present, provided the magnetic
diffusivity is not too small. If the magnetic diffusivity is
smaller, the magnetic field tends to be stronger and can become more
important and may hence be able to suppress this correlation.
Nevertheless, these are also the cases which show most clearly
a systematic magnetic helicity flux within the simulation domain,
even though it is unable to leave or enter it through the boundaries.
It is difficult to say whether the effect of VC2001 was really responsible
for the field generation found in the disc simulations.
We recall that in the present simulations there is also some evidence for a
![]() -effect, although it is based on a rather
noisy correlation between the turbulent electromotive force and the mean
field; see Arlt & Rüdiger (2001).
In the following section we isolate the VC-effect by
studying a more idealized model with no net helicity. This model
also allows for longer runs and therefore clearer statistics.
-effect, although it is based on a rather
noisy correlation between the turbulent electromotive force and the mean
field; see Arlt & Rüdiger (2001).
In the following section we isolate the VC-effect by
studying a more idealized model with no net helicity. This model
also allows for longer runs and therefore clearer statistics.
Copyright ESO 2001