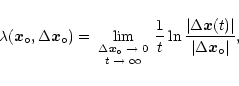 |
(9) |
The next step after the periodic orbit search is to determine the phase space
extent of the regular orbits trapped around the stable closed orbits and of
the chaotic orbits, which have no other integral than the Jacobi integral. The
Poincaré surface of section method is well suited to highlight the regular
and chaotic regions in phase space at constant value of the Hamiltonian, but
not at constant position in real space. A better tool for this purpose are the
Liapunov exponents, which also allow to quantify the degree of stochasticity
of the orbits. These exponents describe the mean exponential rate of
divergence of two trajectories initially close to each other in phase space
and are defined as:
The numerical computation of the Liapunov exponents faces some problems
related to the limits in Eq. (9). First, the finite initial deviation
![]() may rapidly grow as large as the size of the orbits
themselves, especially for chaotic orbits, and thus
may rapidly grow as large as the size of the orbits
themselves, especially for chaotic orbits, and thus
![]() must
be occasionally scaled down by a large factor. Noting
must
be occasionally scaled down by a large factor. Noting
![]() the deviation before the first rescaling, this is done in a way similar to
Contopoulos & Barbanis (1989), by normalising
the deviation before the first rescaling, this is done in a way similar to
Contopoulos & Barbanis (1989), by normalising
![]() to
to
![]() :
:
The Liapunov exponent ![]() has been calculated on a Cartesian grid
of planar velocities for different positions of the observer, using the 2D
potential of Eq. (5) and with an initial deviation of
has been calculated on a Cartesian grid
of planar velocities for different positions of the observer, using the 2D
potential of Eq. (5) and with an initial deviation of
![]() in the R-coordinate
(Figs. 7, 8 and 10). The results are presented
as a divergence timescale
in the R-coordinate
(Figs. 7, 8 and 10). The results are presented
as a divergence timescale
![]() in units of local
circular period in the axisymmetric part of the potential, which provides a
more obvious and useful measure of stochasticity. Diagrams have been computed
for every
in units of local
circular period in the axisymmetric part of the potential, which provides a
more obvious and useful measure of stochasticity. Diagrams have been computed
for every
![]() in azimuth for
in azimuth for
![]() ,
1.0,
1.05, 1.1, 1.2 and also at
,
1.0,
1.05, 1.1, 1.2 and also at
![]() over a larger radial range,
but those diagrams between our
over a larger radial range,
but those diagrams between our
![]() sampling and at
sampling and at
![]() will not be shown here (and the same is true for
the velocity distributions of the next section). We shall refer to such
diagrams as "Liapunov'' diagrams.
will not be shown here (and the same is true for
the velocity distributions of the next section). We shall refer to such
diagrams as "Liapunov'' diagrams.
The first thing to notice in these diagrams is that the stable and
unstable periodic orbits fall within regular and chaotic regions respectively,
as expected. There are some apparent exceptions like the 1/1 asym orbit at
![]() and large R which must owe to the limited velocity resolution of
the diagrams (=0.04
and large R which must owe to the limited velocity resolution of
the diagrams (=0.04![]() ;
see Fux 2001b for some higher resolution
Liapunov diagrams). The fraction of chaotic orbits also obviously increases
with bar strength. Furthermore, as a consequence of the four-fold symmetric
barred potential, the diagrams at
;
see Fux 2001b for some higher resolution
Liapunov diagrams). The fraction of chaotic orbits also obviously increases
with bar strength. Furthermore, as a consequence of the four-fold symmetric
barred potential, the diagrams at ![]() and
and
![]() are symmetric
with respect to u=0 and, more generally, diagrams at supplementary angles
are anti-symmetric to each other in u, i.e.
are symmetric
with respect to u=0 and, more generally, diagrams at supplementary angles
are anti-symmetric to each other in u, i.e.
![]() .
.
At
![]() and for the radial range explored in
Figs. 7 and 8, the 2/1 and 1/1 resonance curves, as
well as all other not highlighted resonances of the form
and for the radial range explored in
Figs. 7 and 8, the 2/1 and 1/1 resonance curves, as
well as all other not highlighted resonances of the form
![]() with
integer
with
integer
![]() ,
are embedded in the middle of broad regular orbit arcs
separated by mainly chaotic regions which come closer to u=0 as the bar
strength increases. For
,
are embedded in the middle of broad regular orbit arcs
separated by mainly chaotic regions which come closer to u=0 as the bar
strength increases. For
![]() (and
(and
![]() ), the regularity of the OLR arc gets destroyed near
u=0, leaving the place to an unstable x1*(2) orbit. Between the dominant
regular orbit arcs, secondary regular arcs associated with resonances of the
form
), the regularity of the OLR arc gets destroyed near
u=0, leaving the place to an unstable x1*(2) orbit. Between the dominant
regular orbit arcs, secondary regular arcs associated with resonances of the
form
![]() with odd integer
with odd integer
![]() can also be identified,
especially for F=0.10. This includes in particular the 4/1 resonance arc
visible for
can also be identified,
especially for F=0.10. This includes in particular the 4/1 resonance arc
visible for
![]() .
In fact, the chaotic regions
between the broad resonance arcs are probably densely filled by tiny arcs of
higher order regular resonant orbits, but the filling factor must be very low.
.
In fact, the chaotic regions
between the broad resonance arcs are probably densely filled by tiny arcs of
higher order regular resonant orbits, but the filling factor must be very low.
At ![]() ,
the situation is reversed: the
,
the situation is reversed: the
![]() resonance
curves lie in chaotic regions at large H which are spaced by regular orbit
arcs right between the resonances. At intermediate angles, the regular and
chaotic regions become offset from the resonance curves and the u-symmetry
breaks. In particular, for
resonance
curves lie in chaotic regions at large H which are spaced by regular orbit
arcs right between the resonances. At intermediate angles, the regular and
chaotic regions become offset from the resonance curves and the u-symmetry
breaks. In particular, for
![]() and
and
![]() ,
i.e. realistic positions for the Sun, an
extreme case of asymmetry arises near the OLR: a prominent region of regular
orbits extends down to negative u, bounded roughly by the OLR curve on the
right and penetrating well inside the hot orbit zone, whereas the positive upart of the OLR curve is surrounded by a wide chaotic region extending
somewhat inside the H12 contour and coinciding very well with the u-vlocation of the Hercules stream.
,
i.e. realistic positions for the Sun, an
extreme case of asymmetry arises near the OLR: a prominent region of regular
orbits extends down to negative u, bounded roughly by the OLR curve on the
right and penetrating well inside the hot orbit zone, whereas the positive upart of the OLR curve is surrounded by a wide chaotic region extending
somewhat inside the H12 contour and coinciding very well with the u-vlocation of the Hercules stream.
![\begin{figure}
\par\includegraphics[width=12cm]{MS1098f09.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg157.gif) |
Figure 9: Location in the u-v plane of the regular orbits trapped around the stable x1(1) periodic orbits for a bar strength F=0.20 (dark points) and around the stable x1(2) orbits for F=0.10 (grey points). The computational details are described in the text. The horizontal and vertical axes of the frames and the different curves are as in Fig. 7. The H-contours are given for F=0.10. |
Figure 9 shows the u-v region occupied by the regular orbits
trapped around the stable x1(1) and x1(2) periodic orbits. To construct
this figure, we have first derived many surfaces of section at mainly constant
Hamiltonian interval
![]() to locate the islands of
invariant curves around these periodic orbits. Then the orbits within each
islands of these maps have been sampled by 50 regularly spaced points along a
straight line across the central periodic orbit and within the outermost
invariant curve of the island. Finally, all the resulting initial conditions
are integrated for 20 rotations in the rotating frame and the velocities are
plotted when the orbits pass within a distance of
to locate the islands of
invariant curves around these periodic orbits. Then the orbits within each
islands of these maps have been sampled by 50 regularly spaced points along a
straight line across the central periodic orbit and within the outermost
invariant curve of the island. Finally, all the resulting initial conditions
are integrated for 20 rotations in the rotating frame and the velocities are
plotted when the orbits pass within a distance of
![]() of the considered space positions. The striped appearance of the regular
x1(1) and x1(2) regions in the diagrams are due to the discrete
H-sampling and the broadening of the stripes to the finite value of
of the considered space positions. The striped appearance of the regular
x1(1) and x1(2) regions in the diagrams are due to the discrete
H-sampling and the broadening of the stripes to the finite value of
![]() (not to an inaccurate orbital integration). The islands in the
surfaces of section generally contain sub-resonances which have been included.
The x1(1) islands however have been truncated at the 1/1 resonance, so
that the part of the x1(1) region on the high-v side of the 1/1resonance curve is not represented in the u-v diagrams. The x1(1) regions
are derived for F=0.20 because the high level of chaos at this bar strength
makes it easier to distinguish the boundaries of these regions in the surfaces
of section, and the x1(2) regions for F=0.10 in order to emphasise the
more regular case where these regions are larger.
(not to an inaccurate orbital integration). The islands in the
surfaces of section generally contain sub-resonances which have been included.
The x1(1) islands however have been truncated at the 1/1 resonance, so
that the part of the x1(1) region on the high-v side of the 1/1resonance curve is not represented in the u-v diagrams. The x1(1) regions
are derived for F=0.20 because the high level of chaos at this bar strength
makes it easier to distinguish the boundaries of these regions in the surfaces
of section, and the x1(2) regions for F=0.10 in order to emphasise the
more regular case where these regions are larger.
From this figure, it is obvious that the regular orbit arcs near the OLR,
and in particular the prominent regular region at
![]() and
and
![]() discussed previously, are produced by the
regular orbits around the stable periodic orbits of the x1(1) family, with
an eccentricity increasing towards larger Hamiltonian values. The regular
regions associated with the stable x1(2) orbits can be viewed as divided
into two parts, one involving only low-eccentricity orbits and the other one
the higher eccentricity orbits falling close to the 4/1 resonance curve. The
low-eccentricity orbit part exists for
discussed previously, are produced by the
regular orbits around the stable periodic orbits of the x1(1) family, with
an eccentricity increasing towards larger Hamiltonian values. The regular
regions associated with the stable x1(2) orbits can be viewed as divided
into two parts, one involving only low-eccentricity orbits and the other one
the higher eccentricity orbits falling close to the 4/1 resonance curve. The
low-eccentricity orbit part exists for
![]() and
over an angle range around
and
over an angle range around
![]() increasing as R decreases,
and is generally enclosed between the H12 contour and the OLR curve.
Elsewhere, it is dissolved and only an unstable x1*(2) orbit remains
(Fig. 7). The higher eccentricity part connects the low-eccentricity
part at
increasing as R decreases,
and is generally enclosed between the H12 contour and the OLR curve.
Elsewhere, it is dissolved and only an unstable x1*(2) orbit remains
(Fig. 7). The higher eccentricity part connects the low-eccentricity
part at
![]() and then progressively detach from
it as the 4/1 resonance curve moves away from the H12 contour at larger
R. In particular, for
and then progressively detach from
it as the 4/1 resonance curve moves away from the H12 contour at larger
R. In particular, for
![]() and for F=0.10,
there are no regular quasi-x1(2) orbits between the H12 contour
and azimuthal velocities less than
and for F=0.10,
there are no regular quasi-x1(2) orbits between the H12 contour
and azimuthal velocities less than
![]() ,
whatever the angle
,
whatever the angle
![]() ,
and no low-eccentricity such orbits at all for
,
and no low-eccentricity such orbits at all for
![]() .
Hence for this bar strength, the Hercules-like mode
found in D2000's simulations at
.
Hence for this bar strength, the Hercules-like mode
found in D2000's simulations at
![]()
![]() and
and
![]() cannot be related to such
quasi-x1(2) orbits.
cannot be related to such
quasi-x1(2) orbits.
![\begin{figure}
\par\includegraphics[width=12cm]{MS1098f10.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg169.gif) |
Figure 10:
As Fig. 7, but for
|
Figure 10 provides Liapunov diagrams over a larger radial range
at
![]() and for F=0.10. These diagrams clearly show that the
H12 contour marks the average transition between regular and chaotic
motion. Hence disc orbits are essentially regular and hot orbits essentially
chaotic. The diagrams in Fig. 10 also nicely illustrate the
dependence of the H12 and H45 contours with galactocentric distance
discussed in Sect. 3, and show how the velocity spacing between
these contours decreases with increasing R.
and for F=0.10. These diagrams clearly show that the
H12 contour marks the average transition between regular and chaotic
motion. Hence disc orbits are essentially regular and hot orbits essentially
chaotic. The diagrams in Fig. 10 also nicely illustrate the
dependence of the H12 and H45 contours with galactocentric distance
discussed in Sect. 3, and show how the velocity spacing between
these contours decreases with increasing R.
Martinet & Raboud (1999) have computed a diagram
![]() representing the relative pericentre deviation between planar orbits
integrated in a barred N-body model and the corresponding orbits in
the underlying axisymmetric potential, starting from a realistic space
position of the Sun. Their diagram correlates well with our Liapunov diagrams
in the sense that the larger values of
representing the relative pericentre deviation between planar orbits
integrated in a barred N-body model and the corresponding orbits in
the underlying axisymmetric potential, starting from a realistic space
position of the Sun. Their diagram correlates well with our Liapunov diagrams
in the sense that the larger values of ![]() coincide with shorter Liapunov
timescales. In particular, a clear jump of
coincide with shorter Liapunov
timescales. In particular, a clear jump of ![]() occurs at
occurs at
![]() ,
with the high-H side displaying much larger
pericentre deviations on the average, and there is also a tail of small
,
with the high-H side displaying much larger
pericentre deviations on the average, and there is also a tail of small
![]() -values at negative u extending inside the hot orbit region.
-values at negative u extending inside the hot orbit region.
It is worth mentioning that in a two-dimensional axisymmetric potential,
all orbits are regular, i.e. have vanishing ![]() .
Hence the chaotic
regions discussed here are all produced by the influence of the bar alone.
Also, the divergence timescale
.
Hence the chaotic
regions discussed here are all produced by the influence of the bar alone.
Also, the divergence timescale
![]() in the chaotic regions may be as
low as a few orbital times. This property may have important consequences on
the early evolution of the distribution function in barred galaxies, as we
shall see in the following section.
in the chaotic regions may be as
low as a few orbital times. This property may have important consequences on
the early evolution of the distribution function in barred galaxies, as we
shall see in the following section.
Copyright ESO 2001