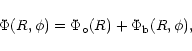Up: Order and chaos in
4 Working potential
The analytical 2D barred potential adopted for the orbital structure analysis
and the test particle simulations is the same as in D2000:
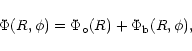 |
(5) |
with
This represents the sum of an axisymmetric potential
 with
constant circular velocity
with
constant circular velocity 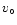 and a barred potential
and a barred potential
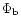 falling off as a quadrupole at
falling off as a quadrupole at 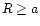 .
The inner and outer parts of the
latter component are described by two distinct functions which connect
together at R=a such as to ensure continuous potential and forces. The bar
major axis is taken to coincide with the y-axis, contrary to the
convention in D2000. The parameter F is the bar strength, defined as the
maximum azimuthal force on the circle of radius a divided by the radial
force of the axisymmetric part of the potential at the same radius (in
absolute value). It is related to Dehnen's parameter
.
The inner and outer parts of the
latter component are described by two distinct functions which connect
together at R=a such as to ensure continuous potential and forces. The bar
major axis is taken to coincide with the y-axis, contrary to the
convention in D2000. The parameter F is the bar strength, defined as the
maximum azimuthal force on the circle of radius a divided by the radial
force of the axisymmetric part of the potential at the same radius (in
absolute value). It is related to Dehnen's parameter 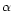 by
by
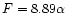 .
The potential is rotating at a constant pattern speed
.
The potential is rotating at a constant pattern speed
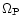 such as to place corotation at
such as to place corotation at
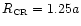 ,
in agreement with numerical simulations and analyses of observations in
early-type barred galaxies if a is associated with the bar semi-major axis
(e.g. Elmegreen 1996). Unlike D2000, only flat rotation curve models will
be examined. In this case, the OLR and corotation radii are related via
,
in agreement with numerical simulations and analyses of observations in
early-type barred galaxies if a is associated with the bar semi-major axis
(e.g. Elmegreen 1996). Unlike D2000, only flat rotation curve models will
be examined. In this case, the OLR and corotation radii are related via
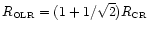 ,
and a value of
,
and a value of
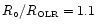 corresponds to a corotation radius
corresponds to a corotation radius
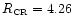 kpc if
kpc if
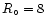 kpc. Some considerations in
the case of a non-constant rotation curve can be found in Sect. 11.
kpc. Some considerations in
the case of a non-constant rotation curve can be found in Sect. 11.
The next sections present a study of the periodic orbits outside
corotation in the adopted rotating barred potential, identify the regular and
chaotic regions in phase space associated with this potential, and discuss how
stars may populate the available orbits. All orbits in these sections are
integrated in double precision using an 8 order Runge-Kutta-Fehlberg algorithm
(Fehlberg 1968). Two values of the bar strength will be considered,
F=0.10 and F=0.20. The larger value corresponds to a rather strong bar
(see Sect. 10 for a quantification with respect to real galaxies),
but has the advantage to clearly point out the effect of chaos in the test
particle simulations. Some of the key results for the intermediate case
F=0.15 are presented in Fux (2001a). For comparison, Dehnen's
simulations were done in the range F=0.062-0.116.


Up: Order and chaos in
Copyright ESO 2001