![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f04new.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg94.gif) |
Figure 4:
Distinct looped periodic orbits in the axisymmetric
potential
|
Much of the orbital structure in a system can be assessed from the study of
its periodic orbits, which sometimes are considered as the skeleton of the
system. While periodic orbits have been widely investigated in 2D and 3D
within bars, only few papers (Athanassoula et al. 1983; Contopoulos &
Grosbol 1989; Sellwood & Wilkinson 1993) discuss them in discs
surrounding bars.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f04new.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg94.gif) |
Figure 4:
Distinct looped periodic orbits in the axisymmetric
potential
|
A good approach to investigate periodic orbits in a 2D rotating barred
potential is to start with the axisymmetric limit. In this case, the only
orbits which close whatever the value of
![]() are the circular
orbits. All other bound orbits can be thought as a libration motion around
these orbits and look like a rosette which never closes, except for some
exceptional potentials like a point mass with
are the circular
orbits. All other bound orbits can be thought as a libration motion around
these orbits and look like a rosette which never closes, except for some
exceptional potentials like a point mass with
![]() ,
or at
resonances, where the radial and azimuthal frequencies
,
or at
resonances, where the radial and azimuthal frequencies
![]() and
and
![]() satisfy the relation:
satisfy the relation:
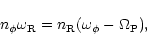 |
(8) |
![\begin{figure}
\par\includegraphics[width=13cm]{MS1098f05new.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg110.gif) |
Figure 5:
a) Characteristic diagram in the rotating axisymmetric
potential (Eq. (6)) for the circular orbit (circ.) and the lowest
order outer
|
The characteristic curves of these resonant orbits in the H-x plane
(Fig. 5a) all intersect the circular orbit curve (COC) at their point
of lowest H, corresponding to a bifurcation. For even resonances, four
branches emanate from the bifurcation, two from the COC and two from the
resonance curve. The resonance branches above (towards larger x) and below
the COC represent orbits with respectively apocentre and pericentre on the
x-axis. The lower branch always passes through the zero velocity
curve (ZVC), where the orbit becomes cuspy on the x-axis and then
develops loops at higher value of the Hamiltonian. For such loop orbits, the
x-coordinate of the characteristic curves does not trace the
pericentre but the place where the orbit self-intersect and
![]() .
For odd resonances, the bifurcation has six branches: the two from the COC,
two for the resonant orbits with radial extrema on the x-axis and
which have properties similar to the former even resonance branches, and two
for the resonant orbits with those extrema on the y-axis. The two
latter branches have opposite
.
For odd resonances, the bifurcation has six branches: the two from the COC,
two for the resonant orbits with radial extrema on the x-axis and
which have properties similar to the former even resonance branches, and two
for the resonant orbits with those extrema on the y-axis. The two
latter branches have opposite ![]() but degenerate into the same curve in
the H-x characteristic diagram. All periodic orbits in the symmetry plane of
an axisymmetric potential are stable.
but degenerate into the same curve in
the H-x characteristic diagram. All periodic orbits in the symmetry plane of
an axisymmetric potential are stable.
Figures 5b and 5c show how the characteristic curves
are modified when the bar component with major axis on the y-axis is
added to the potential. The changes mainly occur at the bifurcations of the
axisymmetric case. The bifurcations of the even resonances become gaps, with
the right (low H) COC branch deviating into the lower resonance branch, and
the upper resonance branch into the left COC branch, giving rise to a sequence
of continuous orbit families. In the terminology introduced by Contopoulos &
Grosbol (1989), the outermost of these families is called x1(1), and
the other families are divided into an upper x1*(i) and a lower x1(i)sub-family at or near the point of minimum H, where the stability of the
orbits appears to reverse. The six-branch bifurcations of the odd resonances
(see the 1/1 and 3/1 resonances in the figures) split into two pitchfork
bifurcations, one involving the resonant orbits symmetric with respect to the
bar minor axis, which are stable near the bifurcation, and the other the
resonant orbits non-symmetric relative to this axis, which are unstable near
the bifurcation and qualified as asymmetric. As a by-product of this
splitting, the segment of the x1(i) characteristic curve between the two
new bifurcations becomes unstable.
At low eccentricity (i.e. small H), only those orbits with a pericentre
on the bar minor axis seem to be stable. This could be the influence of the
Lagrangian points
![]() ,
which are stable fix points in the models. At
high eccentricity, all orbit families undergo a change of stability and the
characteristic curves in Fig. 5 are all interrupted at the point
where the minor axis loop of the orbits touches the centre R=0. The curves
actually go beyond this point, but the resonance number changes. For instance,
the 2/1 orbits become 2/3 orbits. When increasing the bar strength (from
Figs. 5b to 5c), the resonance gaps between successive
x1(i) curves and the separation between the pitchfork bifurcation pairs
increases. The characteristic curves also become more twisted and the fraction
of stable orbits decreases. In particular, almost all x1(3) orbits are
unstable for F=0.20. It should be noted that other authors (Athanassoula et
al. 1983; Sellwood & Wilkinson 1993) report more complicated
characteristic curves for the x1(2) and higher order orbit families near
the ZVC in their models, probably as a consequence of an m=4 Fourier
component in the potential.
,
which are stable fix points in the models. At
high eccentricity, all orbit families undergo a change of stability and the
characteristic curves in Fig. 5 are all interrupted at the point
where the minor axis loop of the orbits touches the centre R=0. The curves
actually go beyond this point, but the resonance number changes. For instance,
the 2/1 orbits become 2/3 orbits. When increasing the bar strength (from
Figs. 5b to 5c), the resonance gaps between successive
x1(i) curves and the separation between the pitchfork bifurcation pairs
increases. The characteristic curves also become more twisted and the fraction
of stable orbits decreases. In particular, almost all x1(3) orbits are
unstable for F=0.20. It should be noted that other authors (Athanassoula et
al. 1983; Sellwood & Wilkinson 1993) report more complicated
characteristic curves for the x1(2) and higher order orbit families near
the ZVC in their models, probably as a consequence of an m=4 Fourier
component in the potential.
Some orbits of the above families are plotted in D2000, but obviously
missing all eccentric x1(1) and x1(2) orbits with loops on the bar minor
axis. A more complete set of orbits from these two families are given in
Fig. 6. These orbits are the most important even ![]() periodic orbits
because they are usually associated with the largest invariant curve islands
in surface of section maps. The orbits drawn with thick lines are examples of
the perpendicularly oriented orbits that replace the circular orbit near the
OLR radius and which have been proposed as a possible explanation for either
the Hyades and Sirius streams (Kalnajs 1991) or the Hercules-LSR
bimodality (D2000) in the observed u-v distribution. As we shall see in the
next sections, the stable eccentric x1(1) orbits also play an important
role in shaping the local velocity distribution. Regular orbits trapped around
them are indeed unlikely to be heavily populated by stars, but represent
forbidden phase space regions for chaotic orbits.
periodic orbits
because they are usually associated with the largest invariant curve islands
in surface of section maps. The orbits drawn with thick lines are examples of
the perpendicularly oriented orbits that replace the circular orbit near the
OLR radius and which have been proposed as a possible explanation for either
the Hyades and Sirius streams (Kalnajs 1991) or the Hercules-LSR
bimodality (D2000) in the observed u-v distribution. As we shall see in the
next sections, the stable eccentric x1(1) orbits also play an important
role in shaping the local velocity distribution. Regular orbits trapped around
them are indeed unlikely to be heavily populated by stars, but represent
forbidden phase space regions for chaotic orbits.
The space coverage of the orbit families can be determined from x-yplots like in Fig. 6. For each position in real space, there will be an
(infinite) set of periodic orbits passing through. The velocity trace in
planar velocity space of the above described orbits, as well as the curves
delineating some of the main resonances in the underlying axisymmetric
potential![]() , are indicated in
Figs. 7 and 8 for various azimuthal angles
, are indicated in
Figs. 7 and 8 for various azimuthal angles ![]() and a
realistic range of galactocentric distances relative to the OLR, and for two
different bar strengths. Here the angle
and a
realistic range of galactocentric distances relative to the OLR, and for two
different bar strengths. Here the angle ![]() is measured from the bar
major axis and increases towards the direction opposite to galactic rotation,
i.e. coincides with the traditional in-plane inclination angle of the bar. All
space positions are reached by many of the considered orbit families, and
sometimes several traces are produced by orbits from the same family: for
instance, at
is measured from the bar
major axis and increases towards the direction opposite to galactic rotation,
i.e. coincides with the traditional in-plane inclination angle of the bar. All
space positions are reached by many of the considered orbit families, and
sometimes several traces are produced by orbits from the same family: for
instance, at
![]() ,
there is a large range of R with three
traces from x1(1) orbits, mainly due to the loops on the x-axis of
the high-H orbits. The traces of the 1/1, 1/1 asym, x1(1),
x1*(2), x1(2) and x1*(3) orbits with non-nearly vanishing
|u|-velocity all fall very close to the associated resonance curves,
indicating that the axisymmetric approximation used to compute these curves
works well for
,
there is a large range of R with three
traces from x1(1) orbits, mainly due to the loops on the x-axis of
the high-H orbits. The traces of the 1/1, 1/1 asym, x1(1),
x1*(2), x1(2) and x1*(3) orbits with non-nearly vanishing
|u|-velocity all fall very close to the associated resonance curves,
indicating that the axisymmetric approximation used to compute these curves
works well for
![]() .
Not all resonant periodic orbits, i.e. those with
traces on the resonance curves, are unstable. In particular, orbits on the
2/1 (OLR) and 1/1 resonance curves are stable x1(1) and 1/1 orbits at
.
Not all resonant periodic orbits, i.e. those with
traces on the resonance curves, are unstable. In particular, orbits on the
2/1 (OLR) and 1/1 resonance curves are stable x1(1) and 1/1 orbits at
![]() and unstable x1*(2) and 1/1 asym orbits at
and unstable x1*(2) and 1/1 asym orbits at
![]() ,
except for a x1*(2) and a x1(1) orbit with u=0for
,
except for a x1*(2) and a x1(1) orbit with u=0for
![]() .
Hence resonance regions of phase space
are not necessary unstable and depleted as asserted in D2000 for the OLR.
.
Hence resonance regions of phase space
are not necessary unstable and depleted as asserted in D2000 for the OLR.
There are sometimes several orbits from the same family plotted very
close to each other, like for example the three unstable x1(2) orbits at
![]() ,
,
![]() and
and
![]() for F=0.20. This happens
when the sequence of orbits within the family reverses its progression in the
x-y plane towards a given direction and very close to the current space
position, causing an accumulation of orbits near this position with different
local velocities. One may also note that the continuous transitions between
some orbit families can cause periodic orbits from different families to have
almost identical traces, as for example the x1*(2) and x1(2) near the
centre of the frame
for F=0.20. This happens
when the sequence of orbits within the family reverses its progression in the
x-y plane towards a given direction and very close to the current space
position, causing an accumulation of orbits near this position with different
local velocities. One may also note that the continuous transitions between
some orbit families can cause periodic orbits from different families to have
almost identical traces, as for example the x1*(2) and x1(2) near the
centre of the frame
![]() and
and
![]() in
Fig. 8.
in
Fig. 8.
![\begin{figure}
\par\includegraphics[width=12cm]{MS1098f08.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg125.gif) |
Figure 8: As Fig. 7, but for a bar strength F=0.20. |
The rather large number of stable simple periodic orbits through each
space position and the numerous stellar streams observed in the Solar
neighbourhood may suggest that at least some of them are related to periodic
orbits, as anticipated in Kalnajs (1991). For instance, beside the idea of
the x1(1) and low-eccentricity x1(2) induced streams near the OLR
radius, the
![]() frames in Fig. 7 betray interesting
stable eccentric x1(2) and 5/1 asym orbits at
frames in Fig. 7 betray interesting
stable eccentric x1(2) and 5/1 asym orbits at
![]() and
and
![]() respectively and
with
respectively and
with
![]() and
and
![]() ,
which fall
very close to the velocity of the young Arcturus stream (see
Table 1).
,
which fall
very close to the velocity of the young Arcturus stream (see
Table 1).
Copyright ESO 2001