- ... Fux
-
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... stream
![[*]](/icons/foot_motif.gif)
- It is
implicitly assumed here that the azimuthal velocity of the Sun is close to the
circular velocity of the axisymmetric part of the Galactic potential. This is
probably correct within 5-10 kms-1, as will be argued in
Sect. 11.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
potential
![[*]](/icons/foot_motif.gif)
- As pointed out in D2000, the Figs. 2 and 4 in
Fux (2000) wrongly display the OLR as a contour of constant H. This
mistake is rectified here throughout the paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1968)
![[*]](/icons/foot_motif.gif)
- In a realistic disc galaxy, the chaotic orbits not confined
within corotation, and in particular the hot chaotic orbits, are not really
bound but their escaping timescale is much larger than the Liapunov divergence
timescale (see also Sect. 7). This is especially true in the case
of our infinite mass logarithmic potential.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
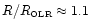
![[*]](/icons/foot_motif.gif)
- More precisely at
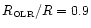 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...u
![[*]](/icons/foot_motif.gif)
- Doubling the average integration time can reinforce the
bimodality, as shown in Fig. 20a.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... resonance
![[*]](/icons/foot_motif.gif)
- This
could be a consequence of the fact that the linear radial oscillation
frequency of the quasi-periodic orbits around the least eccentric stable
x1(2) orbits near the OLR radius, i.e. the non-axisymmetric analogue of the
epicycle frequency for these periodic orbits, is close to the radial frequency
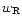 of the x1(2) orbits themselves. A similar argument may also hold for
the slow phase mixing noticed in Fig. 11 within the resonant part
of the quasi-x1(1) region.
of the x1(2) orbits themselves. A similar argument may also hold for
the slow phase mixing noticed in Fig. 11 within the resonant part
of the quasi-x1(1) region.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... contour
![[*]](/icons/foot_motif.gif)
- In particular, at
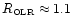 and
and
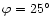 ,
where the low
angular momentum mode has a chaotic origin, the v squashing of the
bimodality reported by D2000 when decreasing his rotation curve parameter
,
where the low
angular momentum mode has a chaotic origin, the v squashing of the
bimodality reported by D2000 when decreasing his rotation curve parameter
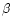 is perhaps not the consequence of a local change of the circular
velocity slope, but of an implied lower relative value of
is perhaps not the consequence of a local change of the circular
velocity slope, but of an implied lower relative value of
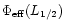 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.