

Up: Order and chaos in
3 Effective potential and Jacobi integral
In a rigid potential
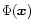 rotating at a constant frequency
rotating at a constant frequency
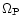 about the z-axis, the Hamiltonian of a test particle
expressed in the rotating frame writes:
about the z-axis, the Hamiltonian of a test particle
expressed in the rotating frame writes:
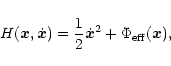 |
(1) |
where
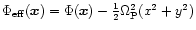 is the effective potential. If
is the effective potential. If
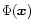 is non-axisymmetric
and
is non-axisymmetric
and
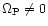 ,
the energy E and the z-component of the
angular momentum Lz are not conserved individually, and the only known
classical integral of motion generally is the value of the Hamiltonian
,
the energy E and the z-component of the
angular momentum Lz are not conserved individually, and the only known
classical integral of motion generally is the value of the Hamiltonian
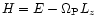 ,
known as the Jacobi integral. Since
,
known as the Jacobi integral. Since
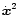 must be positive, this integral restricts the motion of a particle to the
space region where
must be positive, this integral restricts the motion of a particle to the
space region where
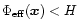 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f02new.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg56.gif) |
Figure 2:
a) Effective potential in the x-y plane of a barred disc
model corresponding to Eq. (5) with F=0.10. The bar is along the
y-axis and the spacing between the contours increases by a factor
1.2 towards lower
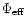 .
The crosses indicate the Lagrangian
points L1/2 (on the y-axis) and L4/5 (on the
x-axis). b) Effective potential along the y-axis
(thick line) and the three main classes of orbits related to the conservation
of the Jacobi integral. The shaded area below the curve is forbidden for
orbits with H<H12. .
The crosses indicate the Lagrangian
points L1/2 (on the y-axis) and L4/5 (on the
x-axis). b) Effective potential along the y-axis
(thick line) and the three main classes of orbits related to the conservation
of the Jacobi integral. The shaded area below the curve is forbidden for
orbits with H<H12. |
In a rotating barred potential, the contours of effective potential in
the plane of symmetry z=0 look like a volcano with a sinusoidal crest, the
extrema of which defining the locations of the Lagrangian points L1/2 and
L4/5, corresponding respectively to the saddle points and maxima of
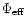 on the major and minor axis of the bar (Fig. 2a).
Two critical values of the Hamiltonian are associated with stars corotating at
these points, namely
on the major and minor axis of the bar (Fig. 2a).
Two critical values of the Hamiltonian are associated with stars corotating at
these points, namely
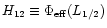 and
and
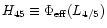 .
The first of them can be used to
classify stellar orbits into three dynamical categories (Sparke & Sellwood
1987; Pfenniger & Friedli 1991): the bar orbits and disc
orbits with H<H12, which cannot cross the H12 contour and are
therefore confined inside and outside corotation respectively, and the hot orbits with
.
The first of them can be used to
classify stellar orbits into three dynamical categories (Sparke & Sellwood
1987; Pfenniger & Friedli 1991): the bar orbits and disc
orbits with H<H12, which cannot cross the H12 contour and are
therefore confined inside and outside corotation respectively, and the hot orbits with
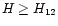 ,
which are susceptible to cross the corotation
barrier and explore all space except a small region around L4/5 if
H<H45 (Fig. 2b). Stars with
H12<H<H45 cannot cross the
corotation radius at all azimuth and may therefore more likely be locked
during several orbital periods on either side of corotation.
,
which are susceptible to cross the corotation
barrier and explore all space except a small region around L4/5 if
H<H45 (Fig. 2b). Stars with
H12<H<H45 cannot cross the
corotation radius at all azimuth and may therefore more likely be locked
during several orbital periods on either side of corotation.
In the Solar neighbourhood, located confidently beyond corotation, only
stars from the disc and hot populations are observed. Since these stars share
about the same
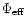 if not too far from the Galactic plane, their
H-values depend mainly on the velocities and thus one expects that the two
populations occupy different regions in local velocity space. If v, u and
w are measured with respect to the Galactic centre, Eq. (1)
transforms into:
if not too far from the Galactic plane, their
H-values depend mainly on the velocities and thus one expects that the two
populations occupy different regions in local velocity space. If v, u and
w are measured with respect to the Galactic centre, Eq. (1)
transforms into:
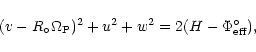 |
(2) |
where 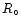 is the galactocentric distance of the Sun and
is the galactocentric distance of the Sun and
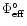 the local effective potential. Thus the contours of
constant Hamiltonian in velocity space are spheres centred on
the local effective potential. Thus the contours of
constant Hamiltonian in velocity space are spheres centred on
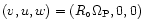 and of radius
and of radius
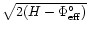 increasing with H. Stars on disc and
hot orbits are respectively those inside and outside the H12 sphere. If
the vertical dimension is neglected, these spheres become circles with the
same properties. In the axisymmetric limit and for a flat rotation curve of
circular velocity
increasing with H. Stars on disc and
hot orbits are respectively those inside and outside the H12 sphere. If
the vertical dimension is neglected, these spheres become circles with the
same properties. In the axisymmetric limit and for a flat rotation curve of
circular velocity 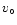 ,
the radius
,
the radius
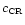 of the
H12=H45 contour and the low azimuthal velocity
of the
H12=H45 contour and the low azimuthal velocity 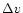 relative to
relative to
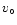 at which this contour crosses the u=0 axis are then given by:
at which this contour crosses the u=0 axis are then given by:
where
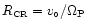 is the corotation radius
(see Fig. 3). For
is the corotation radius
(see Fig. 3). For
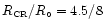 and
and
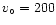 kms-1, one gets
kms-1, one gets
 kms-1, which coincides with the
mean heliocentric asymmetric drift of the Hercules stream
kms-1, which coincides with the
mean heliocentric asymmetric drift of the Hercules stream![[*]](/icons/foot_motif.gif) . Note however that this simple approximation is not truly
a lower limit to the asymmetric drift of stars on hot orbits for several
reasons: a non-zero w velocity component defines two circles on the H12sphere with a reduced projected radius on the u-v plane (small effect, of
order 1 kms-1 for |w|=20 kms-1), the presence of a bar
lowers the effective potential at L1/2 (larger effect, of order
5-10 kms-1), and finally
. Note however that this simple approximation is not truly
a lower limit to the asymmetric drift of stars on hot orbits for several
reasons: a non-zero w velocity component defines two circles on the H12sphere with a reduced projected radius on the u-v plane (small effect, of
order 1 kms-1 for |w|=20 kms-1), the presence of a bar
lowers the effective potential at L1/2 (larger effect, of order
5-10 kms-1), and finally
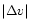 is smaller if
is smaller if 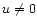 .
Hence
most stars in the Hercules stream are likely to fall outside the H12sphere and therefore may belong to the hot population.
.
Hence
most stars in the Hercules stream are likely to fall outside the H12sphere and therefore may belong to the hot population.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f03.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg77.gif) |
Figure 3:
Contours of constant Hamiltonian in the u-v plane of a realistic 2D
barred model (Eq. (5) with
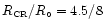 , ,
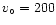 kms-1 and F=0.20). The velocities are relative to an
inertial frame. The inner and outer solid circles give the H12 and
H45 contours respectively, and the dotted circle is the axisymmetric
limit of these contours. kms-1 and F=0.20). The velocities are relative to an
inertial frame. The inner and outer solid circles give the H12 and
H45 contours respectively, and the dotted circle is the axisymmetric
limit of these contours. |
From Eqs. (3) and (4), it also follows that the radius
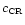 and the velocity separation
and the velocity separation
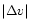 increase for
larger galactocentric distances relative to
increase for
larger galactocentric distances relative to
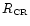 .
In
particular, whatever the strength of the bar, one can always increase the
fraction of the Hercules stream falling in the hot orbit region by reducing
the value of
.
In
particular, whatever the strength of the bar, one can always increase the
fraction of the Hercules stream falling in the hot orbit region by reducing
the value of
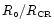 .
.


Up: Order and chaos in
Copyright ESO 2001
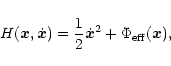
![]() on the major and minor axis of the bar (Fig. 2a).
Two critical values of the Hamiltonian are associated with stars corotating at
these points, namely
on the major and minor axis of the bar (Fig. 2a).
Two critical values of the Hamiltonian are associated with stars corotating at
these points, namely
![]() and
and
![]() .
The first of them can be used to
classify stellar orbits into three dynamical categories (Sparke & Sellwood
1987; Pfenniger & Friedli 1991): the bar orbits and disc
orbits with H<H12, which cannot cross the H12 contour and are
therefore confined inside and outside corotation respectively, and the hot orbits with
.
The first of them can be used to
classify stellar orbits into three dynamical categories (Sparke & Sellwood
1987; Pfenniger & Friedli 1991): the bar orbits and disc
orbits with H<H12, which cannot cross the H12 contour and are
therefore confined inside and outside corotation respectively, and the hot orbits with
![]() ,
which are susceptible to cross the corotation
barrier and explore all space except a small region around L4/5 if
H<H45 (Fig. 2b). Stars with
H12<H<H45 cannot cross the
corotation radius at all azimuth and may therefore more likely be locked
during several orbital periods on either side of corotation.
,
which are susceptible to cross the corotation
barrier and explore all space except a small region around L4/5 if
H<H45 (Fig. 2b). Stars with
H12<H<H45 cannot cross the
corotation radius at all azimuth and may therefore more likely be locked
during several orbital periods on either side of corotation.
![]() if not too far from the Galactic plane, their
H-values depend mainly on the velocities and thus one expects that the two
populations occupy different regions in local velocity space. If v, u and
w are measured with respect to the Galactic centre, Eq. (1)
transforms into:
if not too far from the Galactic plane, their
H-values depend mainly on the velocities and thus one expects that the two
populations occupy different regions in local velocity space. If v, u and
w are measured with respect to the Galactic centre, Eq. (1)
transforms into:
![]() and the velocity separation
and the velocity separation
![]() increase for
larger galactocentric distances relative to
increase for
larger galactocentric distances relative to
![]() .
In
particular, whatever the strength of the bar, one can always increase the
fraction of the Hercules stream falling in the hot orbit region by reducing
the value of
.
In
particular, whatever the strength of the bar, one can always increase the
fraction of the Hercules stream falling in the hot orbit region by reducing
the value of
![]() .
.