10
In addition to the test particle simulations, we have also run a
high-resolution N-body simulation whose predictions can be compared
with the results of the former sections. The main difference of this
simulation with respect to the previous simulations is that it is
three-dimensional and completely self-consistent, i.e. with no rigid component
and allowing the development of spiral arms. The description of the simulation
hereafter is based on physical units in which the initial conditions provide a
reasonable axisymmetric model of the present Milky Way. In these units,
![]() kpc at t=2.32 Gyr.
kpc at t=2.32 Gyr.
The simulation, also discussed in Fux (2000), is similar to the
simulations presented in Fux (1997), starting from a bar unstable
axisymmetric model including a nucleus-spheroid, a disc and a dark halo
component with parameters set to a=1 kpc,
![]() ,
,
![]() kpc, hz=300 pc,
kpc, hz=300 pc,
![]() ,
b=9.1 kpc and
,
b=9.1 kpc and
![]() (in the same notation as in Fux
1997). It involves
(in the same notation as in Fux
1997). It involves
![]() particles of which
particles of which
![]() belong
to the disc component. The simulation uses the double polar-cylindrical grid
technique described in Fux (1999) to solve the gravitational forces, with
belong
to the disc component. The simulation uses the double polar-cylindrical grid
technique described in Fux (1999) to solve the gravitational forces, with
![]() ,
Hz=25 pc and imposed
reflection symmetry with respect to the plane z=0 and the z-axis.
The time integrator is a leap-frog with a time step
,
Hz=25 pc and imposed
reflection symmetry with respect to the plane z=0 and the z-axis.
The time integrator is a leap-frog with a time step
![]() Myr. The
simulation has been carried out until t=2.65 Gyr. The phase space
coordinates have been saved every 50 Myr for all particles and every Myr for
the disc particles within a fixed annulus
Myr. The
simulation has been carried out until t=2.65 Gyr. The phase space
coordinates have been saved every 50 Myr for all particles and every Myr for
the disc particles within a fixed annulus
![]() .
.
After the formation of the bar at about 1.4 Gyr, the simulation reveals
a complex velocity structure with multiple streams occuring almost everywhere
in the disc. The streams, as well as the velocity dispersions, remain very
time dependent, even within space regions corotating with the bar. Some mpeg
movies showing the time evolution of the u-v distribution for a realistic
position of the Sun are available on the web at the address
http://www.mso.anu.edu.au/~fux/streams.html. However, the strong time dependency is certainly partly the consequence of
incomplete phase mixing as in the test particle simulations of the previous
sections. Therefore, we will again average in time the u-v distributions
resulting from the N-body simulation to minimise this problem and
thus focus on the average properties of these distributions.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS1098f16.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg244.gif) |
Figure 16:
Some properties of the N-body simulation averaged over
|
A complication arises from the fact that the pattern speed of the bar
decreases with time due to the angular momentum the bar loses to the (live)
dark halo, so that the OLR does not lie at a fixed radius anymore but moves
outwards. The decrease of
![]() is probably not that large in real
disc galaxies with a substantial gas fraction like the Milky Way, as shown by
self-consistent numerical simulations with an SPH component (e.g. Friedli &
Benz 1993). Hence, the u-v distributions at a given
is probably not that large in real
disc galaxies with a substantial gas fraction like the Milky Way, as shown by
self-consistent numerical simulations with an SPH component (e.g. Friedli &
Benz 1993). Hence, the u-v distributions at a given
![]() must be computed within space volumes
comoving with
must be computed within space volumes
comoving with
![]() .
We found that the evolution of the bar
position angle
.
We found that the evolution of the bar
position angle
![]() over the time interval
over the time interval
![]() can be well fitted by an analytical function of
the form:
can be well fitted by an analytical function of
the form:
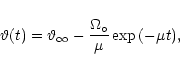 |
(13) |
The time average is done over the interval
![]() and as underlying mass distribution and potential associated with the average
velocity distributions, we take those resulting from the sum of the 50 Myr
spaced output models of the simulation within the same time interval and with
the mass in each model rescaled as the distances to preserve the velocity
scale. The number of models added together is rather low (only 14), yielding
only a crude estimate of the true average quantities, especially regarding
azimuthal variations in the spiral arm regions. Figure 16 shows some
properties of the resulting average model. At given radius R, the azimuthal
and radial bar strengths
and as underlying mass distribution and potential associated with the average
velocity distributions, we take those resulting from the sum of the 50 Myr
spaced output models of the simulation within the same time interval and with
the mass in each model rescaled as the distances to preserve the velocity
scale. The number of models added together is rather low (only 14), yielding
only a crude estimate of the true average quantities, especially regarding
azimuthal variations in the spiral arm regions. Figure 16 shows some
properties of the resulting average model. At given radius R, the azimuthal
and radial bar strengths
![]() and
and
![]() (Fig. 16e) are
defined as the most extreme values over azimuth of
(Fig. 16e) are
defined as the most extreme values over azimuth of
![]() and
and
![]() respectively, where
respectively, where
![]() and
and ![]() are the azimuthal and radial accelerations in the plane
z=0 and
are the azimuthal and radial accelerations in the plane
z=0 and
![]() is the axisymmetric part of
is the axisymmetric part of ![]() .
In particular,
.
In particular,
![]() coincides with the definition of bar
strength used in the former sections. The time averaged model has
coincides with the definition of bar
strength used in the former sections. The time averaged model has
![]() ,
i.e. a rather strong bar. However, Buta &
Block (2001) have introduced a bar strength classification in terms of a
parameter
,
i.e. a rather strong bar. However, Buta &
Block (2001) have introduced a bar strength classification in terms of a
parameter ![]() ,
corresponding here to the radial maximum of
,
corresponding here to the radial maximum of
![]() ,
and present galaxies with values of this parameter up to
0.65. Our average model has
,
and present galaxies with values of this parameter up to
0.65. Our average model has
![]() and thus falls only in
the middle of the range covered by real galaxies.
and thus falls only in
the middle of the range covered by real galaxies.
The disc scale length between corotation and slightly outside the OLR (Fig. 16a) has substantially increased with respect to the initial conditions, in agreement with the test particle results. The effective potential (Fig. 16b) indicates Lagrangian points which significantly lag the bar principal axes. This is the effect of the spiral arms starting at the end of the bar, which were absent in the test particle simulations and now produce a twist of the potential well. Note however that, as pointed out by Zhang (1996), there is a phase shift between the potential and the density wells, with the former leading the latter outside the bar. The characteristic curves of the main periodic orbit families and the x-yconfiguration of the x1(1) orbits in the average potential are given in Fig. 17. The characteristic curves are truncated at large H, where they start to bend and interfere with each other presumably as a consequence of the sharp phase change in the potential well at large radii (see Fig. 16b). The x1(1) orbits respond to the twisted potential well by having their major axis departing more and more from the y-axis as H decreases, and the closed orbits of the other families share a similar response. Since the cusps of the cusped orbits now occur away from the coordinate axes, the characteristic curves no longer reach the ZVC.
The time averaged u-v distributions are presented in Fig. 18.
The diagrams are computed by summing the 1 Myr spaced outputs of the
simulation, yielding much more accurate time averages than for the properties
based on the 50 Myr spaced outputs, and using the same space volumes,
velocity binning and smoothing procedure as for the test particle simulations.
However, contrary to the latter simulations, the diagrams are based on a
unique simulation and therefore the initial conditions for each diagram now
scale as
![]() instead of
instead of ![]() .
Hence the pattern
speed and size of the bar are not the only parameters that change for
different values of
.
Hence the pattern
speed and size of the bar are not the only parameters that change for
different values of
![]() .
In particular, the
initial velocity dispersions decrease with R, causing a similar trend in the
final velocity distributions. Diagrams have been derived at an azimuthal
interval
.
In particular, the
initial velocity dispersions decrease with R, causing a similar trend in the
final velocity distributions. Diagrams have been derived at an azimuthal
interval
![]() ,
but only those at
,
but only those at
![]() spacing
are shown.
spacing
are shown.
![\begin{figure}
\par\includegraphics[width=13cm]{MS1098f18.eps}\end{figure}](/articles/aa/full/2001/26/aa1098/Timg271.gif) |
Figure 18:
Time averaged planar velocity distribution of the disc particles in
the N-body simulation as a function of position in space and within
vertical cylinders of radius
|
A priori, some properties inferred from the test particle simulations
seem less robust in the N-body simulation: the non-resonant x1(1)orbits are somewhat less coincident with peaks in the velocity distributions,
and the resonant x1(1) orbits, i.e. those with traces on the 2/1resonance curve, are less correlated with depleted u-v regions at high
eccentricities. Moreover, the low angular momentum peak often lies well inside
the hot orbit region even when it is still mostly associated with regular
quasi-x1(2) orbits, as indicated by the presence of a stable
low-eccentricity x1(2) orbit. In fact, a closer inspection reveals that the
velocity distributions in the N-body simulation at given
![]() appear to best match those of the test
particle simulations at a typically 10% larger value of
appear to best match those of the test
particle simulations at a typically 10% larger value of
![]() .
This can be explained by a delayed response
of the phase space density distribution to the growing absolute OLR radius:
the u-v distributions do not instantaneously adjust to the moving
.
This can be explained by a delayed response
of the phase space density distribution to the growing absolute OLR radius:
the u-v distributions do not instantaneously adjust to the moving
![]() and therefore always reflect an earlier smaller
and therefore always reflect an earlier smaller
![]() value instead of the current one. Hence the velocity
distributions in Fig. 18 should virtually be shifted upwards by
roughly one frame to be more consistent with the
value instead of the current one. Hence the velocity
distributions in Fig. 18 should virtually be shifted upwards by
roughly one frame to be more consistent with the
![]() scale and the other plotted informations.
Actually, the effective
scale and the other plotted informations.
Actually, the effective
![]() must be a function of the
orbits.
must be a function of the
orbits.
With such a correction in mind, the N-body velocity
distributions now share much more the same properties as in the test particle
simulations. The low angular momentum mode, when purely induced by chaotic
orbits as in the frame
![]() and
and
![]() of Fig. 18, also no longer peaks outside the
H45 contour, but rather between the H12 and the H45 contours.
The velocity distributions most resemble those of the test particle
simulations with a bar strength F=0.15 (not shown in this paper, but see
Fux 2001a). Since
of Fig. 18, also no longer peaks outside the
H45 contour, but rather between the H12 and the H45 contours.
The velocity distributions most resemble those of the test particle
simulations with a bar strength F=0.15 (not shown in this paper, but see
Fux 2001a). Since
![]() in our average N-body model,
this suggests that the velocity distributions are less responsive to the bar
strength in the more realistic 3D N-body simulation than in the 2D
test particle simulations.
in our average N-body model,
this suggests that the velocity distributions are less responsive to the bar
strength in the more realistic 3D N-body simulation than in the 2D
test particle simulations.
The symmetries found in Sect. 7 for the velocity
distributions, and in particular the u-symmetry at ![]() and
and
![]() ,
obviously break and the velocity distributions in the
N-body model at given
,
obviously break and the velocity distributions in the
N-body model at given ![]() and fixed effective radius seem to
compare best with the corresponding distributions in the test particle
simulations at an angle
and fixed effective radius seem to
compare best with the corresponding distributions in the test particle
simulations at an angle
![]() ,
suggesting that the velocity
distributions know about the spiral arm induced average local twist of the
potential well relative to the bar major axis. While this is especially true
for the more regular low-H regions, the velocity distributions show no
significant phase shift at all in the hot orbit region. The reason is because
the hot orbits are more eccentric and therefore are sensitive to more inner
features of the potential. It should be noted that in N-body
simulations like the one presented here, spiral arms are particularly strong
during about 1 Gyr after the formation of the bar, so that the reported
effects of spiral arms are probably overestimates for the Milky Way if the
Galactic bar is old.
,
suggesting that the velocity
distributions know about the spiral arm induced average local twist of the
potential well relative to the bar major axis. While this is especially true
for the more regular low-H regions, the velocity distributions show no
significant phase shift at all in the hot orbit region. The reason is because
the hot orbits are more eccentric and therefore are sensitive to more inner
features of the potential. It should be noted that in N-body
simulations like the one presented here, spiral arms are particularly strong
during about 1 Gyr after the formation of the bar, so that the reported
effects of spiral arms are probably overestimates for the Milky Way if the
Galactic bar is old.
A potentially important difference of 3D models with respect to 2D models
is that the effective potential a star experiences near corotation depends on
its distance from the Galactic plane (see Fig. 16c). This raises the
average value of the Jacobi integral required for the stars to cross the
corotation radius and thus renders such a crossing more difficult. For stars
on the Solar circle, the higher effective value of H12 is not compensated
by their departure from the Galactic plane or a w velocity component.
Indeed, in our average N-body model, the change of effective
potential near corotation when moving from z=0 to z=300 pc is
![]() (with
(with
![]() as defined in the caption of Fig. 17), while
this change at the OLR of the axisymmetrised potential is only 0.004, and
adding a vertical velocity of
as defined in the caption of Fig. 17), while
this change at the OLR of the axisymmetrised potential is only 0.004, and
adding a vertical velocity of
![]() only increases
only increases
![]() by 0.005. Hence 2D models certainly exaggerate
the traffic of stars on hot orbits travelling from one side of corotation to
the other.
by 0.005. Hence 2D models certainly exaggerate
the traffic of stars on hot orbits travelling from one side of corotation to
the other.
Finally, Fig. 19 shows how the value of the Hamiltonian is
conserved during the N-body simulation. The main result is that the
H-values at different times are much better related for bar particles than
for (the dynamically defined) disc and hot particles. In particular, bar
particles remain bar particles, but disc particles can easily transform into
hot particles and vice versa for
![]() ,
supporting the
presumption in Sect. 7 that spiral arms may induce exchanges
between regular and chaotic phase space regions in real galaxies. Near the
1/1 resonance, the disc particles also reveal a smaller scatter of their
past versus present H relation. The normalised Hamiltonian (as well as the
absolute non-rescaled Hamiltonian) increases on the average for the disc
particles, which may be understood by the fact that the contribution of the
term
,
supporting the
presumption in Sect. 7 that spiral arms may induce exchanges
between regular and chaotic phase space regions in real galaxies. Near the
1/1 resonance, the disc particles also reveal a smaller scatter of their
past versus present H relation. The normalised Hamiltonian (as well as the
absolute non-rescaled Hamiltonian) increases on the average for the disc
particles, which may be understood by the fact that the contribution of the
term
![]() to
to
![]() diminishes as the bar
rotates slower, and decreases for the bar particles, owing to the deepening
of the central potential well.
diminishes as the bar
rotates slower, and decreases for the bar particles, owing to the deepening
of the central potential well.
It would be interesting to investigate the evolution of the particle H-values in an N-body simulation with a bar rotating at a constant frequency, for example without including a live dark halo component, in order to disentangle the effects of the spiral arms from the effects of a decreasing pattern speed. It would be also worth to explore the diffusion of particles from regular to chaotic phase space regions and vice versa, starting with 2D N-body simulations in a first approach. One problem to be clarified is why the N-body velocity distributions look so similar to the test particle ones, despite the action of such a diffusion process. A detailed analysis of the orbital structure in 3D models remains to be done, and in particular of the properties of the vertical motion within regular and chaotic regions.
Copyright ESO 2001