

Up: Smooth maps from clumpy
6 Moments expansion
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1052f4.eps} \end{figure}](/articles/aa/full/2001/25/aa1052/Timg152.gif) |
Figure 2:
The effective weight
 can be well
approximated using the expansion (66). This plot shows
the behavior of the n-th order expansion for a Gaussian weight
function with unit variance (see Eq. (75)). The
density used,
can be well
approximated using the expansion (66). This plot shows
the behavior of the n-th order expansion for a Gaussian weight
function with unit variance (see Eq. (75)). The
density used,
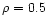 ,
corresponds to ,
corresponds to
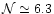 .
The convergence is already extremely good at the second
order; for larger values of .
The convergence is already extremely good at the second
order; for larger values of
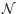 the expansion
converges more rapidly.
the expansion
converges more rapidly. |
In the last section we obtained an analytical expansion for Q(s)which has then been used to obtain a first approximation for the
correction function C(w) valid for large densities 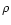 .
Unfortunately, we have been able to obtain a simple result for C(w)only to first order. Already at the second order, in fact, the
correcting function would result in a rather complicated expression
involving the error function erf.
.
Unfortunately, we have been able to obtain a simple result for C(w)only to first order. Already at the second order, in fact, the
correcting function would result in a rather complicated expression
involving the error function erf.
Actually, there is a simpler approach to obtain an expansion of C(w)at large 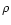 using the moments of the random variable y. Given
the definition (9) for y, we expect that
using the moments of the random variable y. Given
the definition (9) for y, we expect that
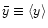 ,
the average value of this random variable,
increases linearly with the density
,
the average value of this random variable,
increases linearly with the density 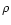 of objects. Similarly, for
large
of objects. Similarly, for
large 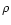 the relative scatter
the relative scatter
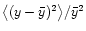 is expected to decrease. In fact, y is the
sum of several independent random variables, and thus, in virtue of
the central limit theorem, it must converge to a Gaussian random
variable with appropriate average and variance.
is expected to decrease. In fact, y is the
sum of several independent random variables, and thus, in virtue of
the central limit theorem, it must converge to a Gaussian random
variable with appropriate average and variance.
Since the relative variance of y decreases with 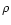 ,
we can
expand y in the denominator in Eq. (14), obtaining
,
we can
expand y in the denominator in Eq. (14), obtaining
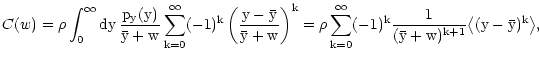 |
|
|
(54) |
where we have used the definition of the moments of y:
In other words, if we are able to evaluate the moments of y we can
obtain an expansion of C(w). Actually, the "centered'' moments can
be calculated from the "un-centered'' ones, defined by
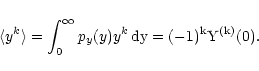 |
(57) |
Here we have used the notation
Y(k)(0) for the k-th derivative
of Y(s) evaluated at s = 0. Using Eq. (19) we can
explicitly write the first few derivatives
| Y(0) =1 , |
(58) |
Y'(0) =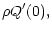 |
(59) |
Y''(0) =![$\displaystyle \rho Q''(0) + \rho^2 \bigl[ Q'(0) \bigr]^2 ,$](/articles/aa/full/2001/25/aa1052/img162.gif) |
(60) |
Y'''(0) =![$\displaystyle \rho Q'''(0) + 3 \rho^2 Q''(0) Q'(0) + \rho^3 \bigl[
Q'(0) \bigr]^3 ,$](/articles/aa/full/2001/25/aa1052/img163.gif) |
(61) |
Y(4)(0) =![$\displaystyle \rho Q^{(4)}(0) + 4 \rho^2 Q'''(0) Q'(0) + 3 \rho^2
\bigl[ Q''(0) \bigr]^2 + 6 \rho^3 Q''(0) \bigl[ Q'(0) \bigr]^2 + \rho^4 \bigl[ Q'(0)
\bigr]^4 .$](/articles/aa/full/2001/25/aa1052/img164.gif) |
(62) |
A nice point here is that, in principle, we can evaluate all the
derivatives of Y(s) in terms of derivatives of Q(s) without any
technical problem. Moreover, the derivatives of Q(s) in zero are
actually directly related to the moments of w. In fact we have
![\begin{displaymath}
Q^{(k)}(0) = (-1)^k \int_\Omega \bigl[w(\vec\theta) \bigr]^k \, \rm d^2
\theta = (-1)^k S_k .
\end{displaymath}](/articles/aa/full/2001/25/aa1052/img165.gif) |
(63) |
This simple relation allows us to express the moments of y in terms
of the moments of w. For the first "centered'' moments we find in
particular
Hence, we finally have
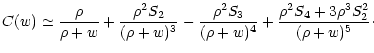 |
|
|
(66) |
The first term if this expansion,
 ,
has already
been obtained in Eq. (51). Other terms represent higher
order corrections to C(w). In Fig. 2 we show the result
of applying this expansion to a Gaussian weight.
,
has already
been obtained in Eq. (51). Other terms represent higher
order corrections to C(w). In Fig. 2 we show the result
of applying this expansion to a Gaussian weight.
In closing this section we note that, regardless of the value of  ,
,
 is vanishing at all orders for
is vanishing at all orders for
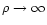 ,
and thus we cannot see the peculiarities of
finite-support weight functions here.
,
and thus we cannot see the peculiarities of
finite-support weight functions here.


Up: Smooth maps from clumpy
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1052f4.eps} \end{figure}](/articles/aa/full/2001/25/aa1052/Timg152.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1052f4.eps} \end{figure}](/articles/aa/full/2001/25/aa1052/Timg152.gif)
![]() .
Unfortunately, we have been able to obtain a simple result for C(w)only to first order. Already at the second order, in fact, the
correcting function would result in a rather complicated expression
involving the error function erf.
.
Unfortunately, we have been able to obtain a simple result for C(w)only to first order. Already at the second order, in fact, the
correcting function would result in a rather complicated expression
involving the error function erf.
![]() using the moments of the random variable y. Given
the definition (9) for y, we expect that
using the moments of the random variable y. Given
the definition (9) for y, we expect that
![]() ,
the average value of this random variable,
increases linearly with the density
,
the average value of this random variable,
increases linearly with the density ![]() of objects. Similarly, for
large
of objects. Similarly, for
large ![]() the relative scatter
the relative scatter
![]() is expected to decrease. In fact, y is the
sum of several independent random variables, and thus, in virtue of
the central limit theorem, it must converge to a Gaussian random
variable with appropriate average and variance.
is expected to decrease. In fact, y is the
sum of several independent random variables, and thus, in virtue of
the central limit theorem, it must converge to a Gaussian random
variable with appropriate average and variance.
![]() ,
we can
expand y in the denominator in Eq. (14), obtaining
,
we can
expand y in the denominator in Eq. (14), obtaining
![]() ,
,
![]() is vanishing at all orders for
is vanishing at all orders for
![]() ,
and thus we cannot see the peculiarities of
finite-support weight functions here.
,
and thus we cannot see the peculiarities of
finite-support weight functions here.