

Up: Smooth maps from clumpy
Subsections
5 Properties
In this section we show a number of interesting properties of C(w)and
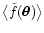 .
.
5.1 Normalization
As already shown [see above Eq. (13)],
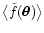 is a simple convolution of
is a simple convolution of
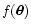 with
with
 .
The normalization I of this convolution can
be obtained from the expression
.
The normalization I of this convolution can
be obtained from the expression
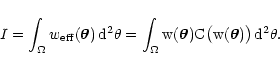 |
(35) |
From Eq. (34) we find
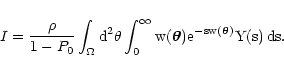 |
(36) |
We first note that, in the general case, Y(s) depends on
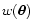 .
On the other hand, since the second term of Y(s)is proportional to
.
On the other hand, since the second term of Y(s)is proportional to 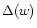 [see Eq. (33)], it does not
contribute to the integral. We can then evaluate first the integral
over
[see Eq. (33)], it does not
contribute to the integral. We can then evaluate first the integral
over
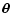 ,
obtaining
,
obtaining
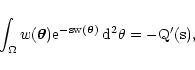 |
(37) |
and thus we have
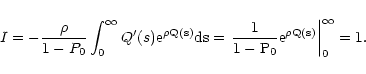 |
(38) |
Hence we conclude that the estimator (5) is correctly
normalized.
5.2 Scaling
It is easily verified that a simple scaling property holds for the
effective weight. Suppose that we evaluate
 for a given weight function
for a given weight function
 and density
and density 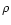 .
If we rescale the weight function
into
.
If we rescale the weight function
into
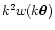 ,
and the density into
,
and the density into 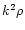 ,
where kis a positive factor, the corresponding effective weight is also
rescaled similarly to w, i.e.
,
where kis a positive factor, the corresponding effective weight is also
rescaled similarly to w, i.e.
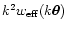 .
.
We also recall here that, although a normalized weight function has
been assumed [see Eq. (6)], all results are clearly
independent of the normalization of w. Hence, we can also consider
a trivial scaling property: the weight function
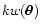 has
effective weight
has
effective weight
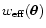 independent of k.
independent of k.
We anticipate that the effective weight is very close to the original
weight w for large densities 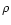 (see below
Sect. 5.4). The scaling properties discussed
above suggest that the shape of the effective weight is actually
controlled by the expected number of objects for which the weight is
significantly different from zero. This justifies the definition of
the weight area
(see below
Sect. 5.4). The scaling properties discussed
above suggest that the shape of the effective weight is actually
controlled by the expected number of objects for which the weight is
significantly different from zero. This justifies the definition of
the weight area
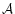 of w:
of w:
![\begin{displaymath}
\mathcal{A} = \biggl[ \int_\Omega w(\vec\theta) \,
\rm d^2...
...ega \bigl[
w(\vec\theta) \bigr]^2 \, \rm d^2 \theta \biggr] .
\end{displaymath}](/articles/aa/full/2001/25/aa1052/img107.gif) |
(39) |
The first factor in this definition ensures that
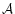 does
not depend on the normalization of
does
not depend on the normalization of
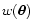 .
It is easily
verified that
.
It is easily
verified that
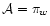 for a top-hat weight function.
Correspondingly, we define the weight number of objects as
for a top-hat weight function.
Correspondingly, we define the weight number of objects as
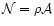 .
Clearly, this quantity is left
unchanged by the scalings considered above. Similar definitions can
be provided for the effective weight
.
Clearly, this quantity is left
unchanged by the scalings considered above. Similar definitions can
be provided for the effective weight
 .
Explicitely,
we have
.
Explicitely,
we have
![\begin{displaymath}
\mathcal{A}_{\rm eff} = \biggl[ \int_\Omega
w_{\rm eff}(\v...
... w_{\rm eff}(\vec\theta) \bigr]^2 \,
\rm d^2 \theta \biggr] ,
\end{displaymath}](/articles/aa/full/2001/25/aa1052/img110.gif) |
(40) |
and
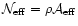 .
.
Numerical calculations for
 show clearly that
show clearly that
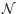 ,
rather than
,
rather than 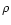 ,
is the key factor that controls
how close the effective weight
,
is the key factor that controls
how close the effective weight
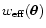 is to
is to
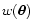 (cf. Figs. 1, 3, and 4).
(cf. Figs. 1, 3, and 4).
5.3 Behavior of w C(w)
We can easily study the general behavior of
 .
We
first consider the case of infinite-support weights (P0 = 0).
.
We
first consider the case of infinite-support weights (P0 = 0).
We first note that Y(s) > 0 for every s, and thus C(w) decreases
as w increases. On the other hand, we have
 .
\end{displaymath}](/articles/aa/full/2001/25/aa1052/img113.gif) |
(41) |
Since
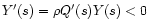 is negative, we have that w C(w)increases with w. This result shows that the effective weight
is negative, we have that w C(w)increases with w. This result shows that the effective weight
 follows the general shape of the weight w, as
expected. Moreover, the fact that C(w) is monotonically decreasing
implies that the effective weight
follows the general shape of the weight w, as
expected. Moreover, the fact that C(w) is monotonically decreasing
implies that the effective weight
 is "broader'' than
w. For instance, we can say that there is a value w1 for the
weight such that
is "broader'' than
w. For instance, we can say that there is a value w1 for the
weight such that
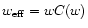 is not larger than w for
w > w1, and not smaller than w for w < w1. In fact, since
C(w) is monotonic, the equation C(w) = 1 can have at most one
solution. On the other hand, if C(w) < 1 (respectively, if C(w) >
1) for all w, then
is not larger than w for
w > w1, and not smaller than w for w < w1. In fact, since
C(w) is monotonic, the equation C(w) = 1 can have at most one
solution. On the other hand, if C(w) < 1 (respectively, if C(w) >
1) for all w, then
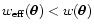 (
(
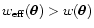 )
for all
)
for all
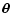 .
This inequality, however, cannot be true since both w and
.
This inequality, however, cannot be true since both w and
 are normalized.
are normalized.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1052f1.eps} \end{figure}](/articles/aa/full/2001/25/aa1052/Timg120.gif) |
Figure 1:
The effective weight
 never exceeds
never exceeds
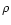 .
The original weight .
The original weight
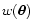 is the combination
of two Gaussians with different widths (
is the combination
of two Gaussians with different widths (
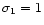 and
and
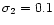 ). The central peak is severely depressed for
relatively low densities. Note that the weight area is ). The central peak is severely depressed for
relatively low densities. Note that the weight area is
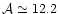 ,
so that a density of ,
so that a density of
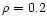 corresponds to
corresponds to
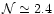 . . |
The property just shown can be used to derive a relation between the
weight area
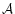 and the effective weight area
and the effective weight area
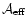 .
Let us evaluate the integral
.
Let us evaluate the integral
![\begin{displaymath}
D = \int_\Omega \bigl[ w(\vec\theta) + w_{\rm eff}(\vec\the...
...c\theta) - w_{\rm eff}(\vec\theta) \bigr]
\, \rm d^2 \theta .
\end{displaymath}](/articles/aa/full/2001/25/aa1052/img122.gif) |
(42) |
This quantity is positive, since the integrand is positive (this is
easily verified by distinguishing the two cases
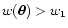 and
and
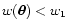 ,
and by noting that both factors in the
integrand have the same sign). On the other hand, if we expand the
product we obtain
,
and by noting that both factors in the
integrand have the same sign). On the other hand, if we expand the
product we obtain
![$\displaystyle 0 < D =\int_\Omega \bigl[ w(\vec\theta) \bigr]^2 \, \rm d^2
\thet...
...eta) \bigr] \, \rm d^2 \theta = \mathcal{A}^{-1} - \mathcal{A}_{\rm eff}^{-1} .$](/articles/aa/full/2001/25/aa1052/img125.gif) |
|
|
(43) |
The last relation holds because of the normalization of
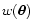 and
and
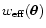 .
We thus have shown
that the effective weight area
.
We thus have shown
that the effective weight area
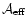 is always
larger than the original weight area
is always
larger than the original weight area
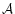 ;
analogously we
have
;
analogously we
have
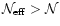 .
This, clearly, is
another indication that
.
This, clearly, is
another indication that
 is "broader'' than w.
is "broader'' than w.
It is also interesting to evaluate the limits of w C(w) for small
and large values of w. We have
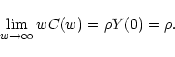 |
(44) |
Since we know that w C(w) is monotonic, 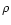 is also a superior
limit for the effective weight function. In other words, even if whas high peaks, the effective weight
is also a superior
limit for the effective weight function. In other words, even if whas high peaks, the effective weight
 (that, we
recall, is normalized) will never exceed the value
(that, we
recall, is normalized) will never exceed the value 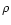 (see
Fig. 1). We stress here that, since
(see
Fig. 1). We stress here that, since
 is
normalized, its maximum value [which, in virtue of Eq. (44)
does not exceed
is
normalized, its maximum value [which, in virtue of Eq. (44)
does not exceed 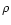 ]
is a significant parameter. For example,
using the relation
]
is a significant parameter. For example,
using the relation
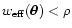 in the
definition of
in the
definition of
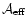 we find immediately
we find immediately
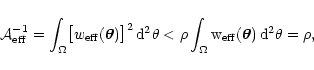 |
(45) |
or, equivalently,
 .
In other words, no
matter how small
.
In other words, no
matter how small
 is, the effective weight will always
"force'' us to use at least one object.
is, the effective weight will always
"force'' us to use at least one object.
Equation (44) suggests also a local
order-of-magnitude check for the effective weight: assuming
 normalized, we expect the effective weight to be
significantly different from w for points where
normalized, we expect the effective weight to be
significantly different from w for points where
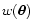 is
of the order of
is
of the order of 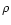 or larger. Equation (45), instead,
provides a global criterion: the effective weight will be
significantly broader than w if
or larger. Equation (45), instead,
provides a global criterion: the effective weight will be
significantly broader than w if
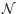 is of the order of
unity or smaller. As anticipated above, thus,
is of the order of
unity or smaller. As anticipated above, thus,
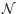 is the
real key factor that controls the shape of
is the
real key factor that controls the shape of
 with
respect to w.
with
respect to w.
The other limit for the effective weight is
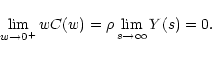 |
(46) |
Thus, as expected, the effective weight
 vanishes as
w vanishes.
vanishes as
w vanishes.
If w has finite support, then the situation is slightly different.
Given the definition of Y(s), we expect for C(w) a discontinuity
for w = 0. Apart from this difference, the behavior of C(w) and
of w C(w) is similar to the case considered above, namely C(w) is
monotonically decreasing and w C(w) is increasing. We also have
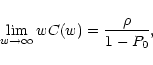 |
(47) |
which is similar to Eq. (44). Note that, as expected from
the normalization of
 ,
,
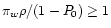 for all densities. We also find
for all densities. We also find
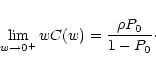 |
(48) |
In other words, the effective weight w C(w) does not
vanish for small w. If, instead, we take w = 0, then we have
w C(w) = 0. This discontinuity, related to the term 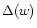 in
Eq. (33), is a consequence of a number of properties for the
effective weight: (i)
in
Eq. (33), is a consequence of a number of properties for the
effective weight: (i)
 is normalized; (ii)
is normalized; (ii)
 is broader than w; (iii)
is broader than w; (iii)
 has the
same support as w. We thus are forced to have a discontinuity for
the effective weight.
The result obtained above is also convenient for simplifying equations
for finite-support weight functions. In fact, for w > 0 we can
clearly drop the last term of Eq. (33), thus recovering
Eq. (19); if, instead, w = 0, we can directly set
w C(w) =
0, without further calculations.
has the
same support as w. We thus are forced to have a discontinuity for
the effective weight.
The result obtained above is also convenient for simplifying equations
for finite-support weight functions. In fact, for w > 0 we can
clearly drop the last term of Eq. (33), thus recovering
Eq. (19); if, instead, w = 0, we can directly set
w C(w) =
0, without further calculations.
5.4 Limit of high and low densities
The final result considered in this section is the behavior of the
correcting factor C(w) in the limit
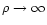 and
and
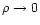 .
.
We observe that
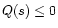 and moreover
and moreover
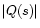 increases with s. Thus, if s is large,
increases with s. Thus, if s is large,
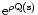 vanishes quickly when
vanishes quickly when
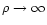 .
As a
result, in the limit of large densities we are mainly interested in
Q(s) with s small. Expanding Q(s) around s = 0+, we find
.
As a
result, in the limit of large densities we are mainly interested in
Q(s) with s small. Expanding Q(s) around s = 0+, we find
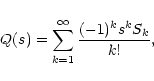 |
(49) |
where Sk is the kth moment of w:
![\begin{displaymath}
S_k = \int_\Omega \bigl[ w(\vec\theta) \bigr]^k \, \rm d^2 \theta
.
\end{displaymath}](/articles/aa/full/2001/25/aa1052/img141.gif) |
(50) |
The normalization of w clearly implies S1 = 1. Assuming w > 0,
to first order we have then
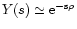 ,
so that
,
so that
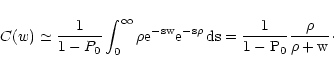 |
(51) |
This expression gives the correcting factor at the first order in
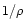 .
If w has infinite support the expression reduces to
.
If w has infinite support the expression reduces to
![$C(w)
= 1 / \bigl[ 1 + w/\rho\bigr]$](/articles/aa/full/2001/25/aa1052/img145.gif) .
Note that the quantity
.
Note that the quantity
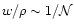 is related the weight number, i.e. the
expected number of objects which contribute significantly to the
signal, for which the weight is not exceedingly small. Finally, at
the zero order in the limit
is related the weight number, i.e. the
expected number of objects which contribute significantly to the
signal, for which the weight is not exceedingly small. Finally, at
the zero order in the limit
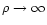 ,
C(w)converges to unity. In this case the map
,
C(w)converges to unity. In this case the map
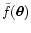 is
expected to be a smoothing of
is
expected to be a smoothing of
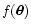 with the same weight
function w.
with the same weight
function w.
In the limit
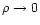 ,
we have
,
we have
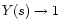 ,
and
thus
,
and
thus
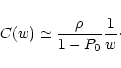 |
(52) |
In the same limit,
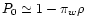 ,
so that we find
,
so that we find
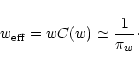 |
(53) |
Recalling that w C(w) vanishes for w = 0, we conclude that the
effective weight converges to a top-hat function with support
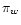 if
if
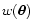 has finite-support (see Fig. 4
for an example).
has finite-support (see Fig. 4
for an example).


Up: Smooth maps from clumpy
Copyright ESO 2001
![]() .
.
![]() is a simple convolution of
is a simple convolution of
![]() with
with
![]() .
The normalization I of this convolution can
be obtained from the expression
.
The normalization I of this convolution can
be obtained from the expression
![]() for a given weight function
for a given weight function
![]() and density
and density ![]() .
If we rescale the weight function
into
.
If we rescale the weight function
into
![]() ,
and the density into
,
and the density into ![]() ,
where kis a positive factor, the corresponding effective weight is also
rescaled similarly to w, i.e.
,
where kis a positive factor, the corresponding effective weight is also
rescaled similarly to w, i.e.
![]() .
.
![]() has
effective weight
has
effective weight
![]() independent of k.
independent of k.
![]() (see below
Sect. 5.4). The scaling properties discussed
above suggest that the shape of the effective weight is actually
controlled by the expected number of objects for which the weight is
significantly different from zero. This justifies the definition of
the weight area
(see below
Sect. 5.4). The scaling properties discussed
above suggest that the shape of the effective weight is actually
controlled by the expected number of objects for which the weight is
significantly different from zero. This justifies the definition of
the weight area
![]() of w:
of w:
![]() show clearly that
show clearly that
![]() ,
rather than
,
rather than ![]() ,
is the key factor that controls
how close the effective weight
,
is the key factor that controls
how close the effective weight
![]() is to
is to
![]() (cf. Figs. 1, 3, and 4).
(cf. Figs. 1, 3, and 4).
![]() .
We
first consider the case of infinite-support weights (P0 = 0).
.
We
first consider the case of infinite-support weights (P0 = 0).
![]() and the effective weight area
and the effective weight area
![]() .
Let us evaluate the integral
.
Let us evaluate the integral
![]() normalized, we expect the effective weight to be
significantly different from w for points where
normalized, we expect the effective weight to be
significantly different from w for points where
![]() is
of the order of
is
of the order of ![]() or larger. Equation (45), instead,
provides a global criterion: the effective weight will be
significantly broader than w if
or larger. Equation (45), instead,
provides a global criterion: the effective weight will be
significantly broader than w if
![]() is of the order of
unity or smaller. As anticipated above, thus,
is of the order of
unity or smaller. As anticipated above, thus,
![]() is the
real key factor that controls the shape of
is the
real key factor that controls the shape of
![]() with
respect to w.
with
respect to w.
![]() and
and
![]() .
.
![]() and moreover
and moreover
![]() increases with s. Thus, if s is large,
increases with s. Thus, if s is large,
![]() vanishes quickly when
vanishes quickly when
![]() .
As a
result, in the limit of large densities we are mainly interested in
Q(s) with s small. Expanding Q(s) around s = 0+, we find
.
As a
result, in the limit of large densities we are mainly interested in
Q(s) with s small. Expanding Q(s) around s = 0+, we find
![]() ,
we have
,
we have
![]() ,
and
thus
,
and
thus