

Up: Smooth maps from clumpy
Subsections
7 Examples
In this section we consider three typical examples of weight
functions, namely a top-hat function, a Gaussian, and a parabolic
weight function. For simplicity, in the following we will consider
weight functions with fixed "width''. The results obtained can
then be adapted to weight functions with different widths using the
scaling property (Sect. 5.2).
7.1 Top-hat
The simplest case we can consider for
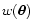 is a top-hat
function of unit radius, which can be written as
is a top-hat
function of unit radius, which can be written as
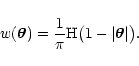 |
(67) |
In this case we immediately find for w > 0
Q(s) =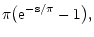 |
(68) |
Y(s) =![$\displaystyle \exp \bigl[ \pi\rho \bigl( \rm e^{-s/\pi} - 1 \bigr) \bigr]
.$](/articles/aa/full/2001/25/aa1052/img176.gif) |
(69) |
We now note that since
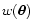 is either 0 or
is either 0 or 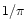 ,
we
just need to evaluate
,
we
just need to evaluate 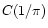 .
We then find
.
We then find
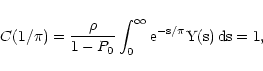 |
(70) |
as expected.
For the top-hat function we can also explicitly obtain the probability
distribution for y. If w > 0 we have
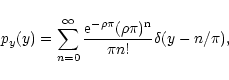 |
(71) |
and thus
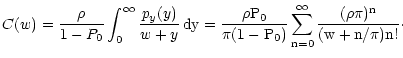 |
|
|
(72) |
From this expression we easily obtain
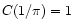 .
Moreover, we can
evaluate the two limits
.
Moreover, we can
evaluate the two limits
thus regaining the results of Sect. 5.3.
7.2 Gaussian
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{1052f2.eps} \end{figure}](/articles/aa/full/2001/25/aa1052/Timg189.gif) |
Figure 3:
Effective weight function corresponding to a Gaussian
weight function. The original weight function is a normalized
Gaussian of unit variance, with weight area
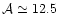 .
Significantly broader effective weights are obtained if
the weight number is smaller than .
Significantly broader effective weights are obtained if
the weight number is smaller than
 . .
|
A weight function commonly used is a Gaussian of the form
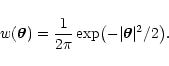 |
(75) |
Unfortunately, we cannot explicitly integrate Q(s) and thus we are
unable to obtain a finite expression for C(w). The results of a
numerical calculations are however shown in Fig. 3.
7.3 Parabolic weight
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1052f3.eps} \end{figure}](/articles/aa/full/2001/25/aa1052/Timg193.gif) |
Figure 4:
Effective weight function corresponding to a Gaussian
weight function. Note the discontinuity at
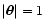 ,
corresponding to the boundary of the support of w. The
original weight function is a normalized parabolic function with
weight area ,
corresponding to the boundary of the support of w. The
original weight function is a normalized parabolic function with
weight area
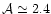 .
Note that this weight
area is significantly smaller than the ones encountered in
previous examples. For low densities, .
Note that this weight
area is significantly smaller than the ones encountered in
previous examples. For low densities,
 converges to a top-hat function, in accordance with the results
of Sect. 5.4.
converges to a top-hat function, in accordance with the results
of Sect. 5.4. |
As the last, example we consider a parabolic weight function with
expression
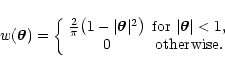 |
(76) |
We then find
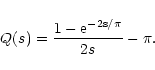 |
(77) |
Unfortunately, we cannot proceed analytically and determine C(w).
We thus report the results of numerical integrations in
Fig. 4. Note that, as expected, the resulting effective
weight has a discontinuity at
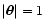 .
.


Up: Smooth maps from clumpy
Copyright ESO 2001
![]() is a top-hat
function of unit radius, which can be written as
is a top-hat
function of unit radius, which can be written as
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1052f3.eps} \end{figure}](/articles/aa/full/2001/25/aa1052/Timg193.gif)