

Up: Smooth maps from clumpy
8 Conclusions
In this paper we have studied from a statistical point of view the
effect of smoothing irregularly sampled data. The main results
obtained can be summarized in the following points.
- 1.
- The mean smooth map,
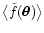 ,
is a convolution of the unknown field
,
is a convolution of the unknown field
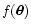 with an effective weight
with an effective weight
 ;
;
- 2.
- We have provided simple expressions to evaluate the effective
weight. These expressions can be easily used, for example, to
obtain numerical estimates of
 ;
;
- 3.
- The effective weight
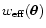 and the weight
function
and the weight
function
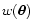 share the same support and have a similar
"shape''. However,
share the same support and have a similar
"shape''. However,
 is broader than w,
expecially for low densities of objects; moreover,
is broader than w,
expecially for low densities of objects; moreover,
 has a discontinuity at the boundary of the support;
has a discontinuity at the boundary of the support;
- 4.
- We have shown that the density of objects
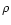 (or
(or
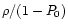 for finite-support weight functions) is a natural
upper limit for the effective weights;
for finite-support weight functions) is a natural
upper limit for the effective weights;
- 5.
- The weight number
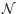 has been shown to be the key
factor that controls the convergence of
has been shown to be the key
factor that controls the convergence of
 to w. We
have also shown that
to w. We
have also shown that
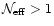 ;
;
- 6.
- The effective weight converges to
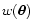 for large
densities
for large
densities 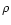 ,
and to a top-hat function for low densities;
,
and to a top-hat function for low densities;
- 7.
- We have provided an analytic expansion for
 which is shown to converge quickly to the exact weight function;
which is shown to converge quickly to the exact weight function;
- 8.
- Finally, we have considered three typical examples and shown the
behavior of
 for different densities.
for different densities.
Given the wide use in astronomy of the smoothing technique considered
in this paper, an exact statistical characterization of the
expectation value of the smoothed map is probably interesting
per se.
Finally, we notice that other methods different from Eqs. (5)
or (3) can be used to obtain continuous maps from irregularly
sampled data. In particular, triangulation techniques can represent
an interesting alternative to the simple weighted average considered
here (see, e.g., Bernardeau & van de Weygaert 1996; Schaap & van de
Weygaert 2000).
Acknowledgements
We would like to thank the Referee for comments and suggestions that
enabled us to improve this paper.


Up: Smooth maps from clumpy
Copyright ESO 2001