A&A 457, 281-308 (2006)
DOI: 10.1051/0004-6361:20054654
R. Buras1,2 -
H.-Th. Janka1 -
M. Rampp1,![]() -
K. Kifonidis1
-
K. Kifonidis1
1 - Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
2 -
Max-Planck-Institut für Physik,
Föhringer Ring 6, 80805 München, Germany
Received 7 December 2005 / Accepted 30 June 2006
Abstract
Spherically symmetric (1D) and two-dimensional (2D) supernova simulations
for progenitor stars between 11![]() and 25
and 25![]() are
presented, making use of the PROMETHEUS/VERTEX
neutrino-hydrodynamics code, which employs a full spectral treatment
of neutrino transport and neutrino-matter interactions with
a variable Eddington factor closure of
the
are
presented, making use of the PROMETHEUS/VERTEX
neutrino-hydrodynamics code, which employs a full spectral treatment
of neutrino transport and neutrino-matter interactions with
a variable Eddington factor closure of
the
![]() moments equations of neutrino number, energy,
and momentum. Multi-dimensional transport aspects are treated by the
"ray-by-ray plus'' approximation described in Paper I.
We discuss in detail the variation of the supernova evolution with the
progenitor models, including one calculation for a 15
moments equations of neutrino number, energy,
and momentum. Multi-dimensional transport aspects are treated by the
"ray-by-ray plus'' approximation described in Paper I.
We discuss in detail the variation of the supernova evolution with the
progenitor models, including one calculation for a 15![]() progenitor whose iron core is assumed to rotate rigidly with an
angular frequency of 0.5 rad s-1 before collapse.
We also test the sensitivity of our 2D calculations to the
angular grid resolution, the lateral wedge size of the computational
domain, and to the perturbations which seed convective instabilities
in the post-bounce core. In particular, we do not find any important
differences depending on whether random perturbations are included
already during core collapse or whether such perturbations are
imposed on a 1D collapse model shortly after core bounce.
Convection below the neutrinosphere sets in 30-40 ms
after bounce at a density well above 1012 g cm-3in all 2D models,
and encompasses a layer of growing mass as time goes on. It leads
to a more extended proto-neutron star structure with reduced mean
energies of the radiated neutrinos, but accelerated lepton
number and energy loss and significantly higher muon and tau neutrino
luminosities
at times later than about 100 ms after bounce. While convection
inside the nascent neutron star turns out to be insensitive to our
variations of the angular cell and grid size, the convective
activity in the neutrino-heated postshock layer gains more
strength in better resolved models. We find that low (l = 1, 2)
convective modes, which require the use of a full 180 degree grid
and are excluded in simulations with smaller angular wedges,
can qualitatively change the evolution of a model. In
case of an
progenitor whose iron core is assumed to rotate rigidly with an
angular frequency of 0.5 rad s-1 before collapse.
We also test the sensitivity of our 2D calculations to the
angular grid resolution, the lateral wedge size of the computational
domain, and to the perturbations which seed convective instabilities
in the post-bounce core. In particular, we do not find any important
differences depending on whether random perturbations are included
already during core collapse or whether such perturbations are
imposed on a 1D collapse model shortly after core bounce.
Convection below the neutrinosphere sets in 30-40 ms
after bounce at a density well above 1012 g cm-3in all 2D models,
and encompasses a layer of growing mass as time goes on. It leads
to a more extended proto-neutron star structure with reduced mean
energies of the radiated neutrinos, but accelerated lepton
number and energy loss and significantly higher muon and tau neutrino
luminosities
at times later than about 100 ms after bounce. While convection
inside the nascent neutron star turns out to be insensitive to our
variations of the angular cell and grid size, the convective
activity in the neutrino-heated postshock layer gains more
strength in better resolved models. We find that low (l = 1, 2)
convective modes, which require the use of a full 180 degree grid
and are excluded in simulations with smaller angular wedges,
can qualitatively change the evolution of a model. In
case of an
![]() star, the lowest-mass progenitor we
investigate, a probably rather weak explosion by the convectively supported
neutrino-heating mechanism develops after about 150 ms post-bounce
evolution in a 2D simulation with 180 degrees, whereas the same
model with 90 degree wedge fails to explode like all other models.
This sensitivity demonstrates the proximity of our 2D calculations to
the borderline between success and failure, and stresses the need to
strive for simulations in 3D, ultimately without the constraints
connected with the axis singularity of a polar coordinate grid.
star, the lowest-mass progenitor we
investigate, a probably rather weak explosion by the convectively supported
neutrino-heating mechanism develops after about 150 ms post-bounce
evolution in a 2D simulation with 180 degrees, whereas the same
model with 90 degree wedge fails to explode like all other models.
This sensitivity demonstrates the proximity of our 2D calculations to
the borderline between success and failure, and stresses the need to
strive for simulations in 3D, ultimately without the constraints
connected with the axis singularity of a polar coordinate grid.
Key words: supernovae: general - neutrinos - radiative transfer - hydrodynamics
The mechanism by which massive stars explode is still unclear.
State-of-the-art models with
a spectral treatment of the neutrino transport by solving the
Boltzmann equation or/and its moments equations agree in the
finding that in
spherical symmetry (1D) neither the prompt bounce-shock mechanism
nor the delayed neutrino-driven mechanism lead to explosions
for progenitors more massive than about 10![]() (e.g., Rampp & Janka 2002; Liebendörfer et al. 2001,2004;
Thompson et al. 2003; Sumiyoshi et al. 2005). Previous
two-dimensional (2D) simulations (e.g., Herant et al. 1994;
Burrows et al. 1995; Janka & Müller 1996; Fryer 1999;
Fryer & Heger 2000) and three-dimensional (3D) models
(Fryer & Warren 2004,2002) show the importance of convective
overturn in the neutrino-heating layer behind the stalled
supernova shock, which can enhance the
energy transfer from neutrinos to the stellar matter
and thus cause "convectively supported neutrino-driven
explosions''. These multi-D models, however, employed radical
simplifications of the treatment of neutrinos, mostly by grey
diffusion or in a parametric way as heating terms. Concerns about
the reliability of such approximations of crucial physics in
studies of the supernova explosion mechanism were expressed by
Mezzacappa et al. (1998).
(e.g., Rampp & Janka 2002; Liebendörfer et al. 2001,2004;
Thompson et al. 2003; Sumiyoshi et al. 2005). Previous
two-dimensional (2D) simulations (e.g., Herant et al. 1994;
Burrows et al. 1995; Janka & Müller 1996; Fryer 1999;
Fryer & Heger 2000) and three-dimensional (3D) models
(Fryer & Warren 2004,2002) show the importance of convective
overturn in the neutrino-heating layer behind the stalled
supernova shock, which can enhance the
energy transfer from neutrinos to the stellar matter
and thus cause "convectively supported neutrino-driven
explosions''. These multi-D models, however, employed radical
simplifications of the treatment of neutrinos, mostly by grey
diffusion or in a parametric way as heating terms. Concerns about
the reliability of such approximations of crucial physics in
studies of the supernova explosion mechanism were expressed by
Mezzacappa et al. (1998).
Also the influence of convective activity inside the nascent neutron star, i.e. below the neutrinosphere, on the explosion mechanism has long been a matter of debate and requires further studies. The Livermore group (Wilson & Mayle 1993,1988) obtained explosions in their basically 1D models by assuming that so-called neutron-finger mixing instabilities exist in the newly formed neutron star, which accelerate the energy transport from the neutron star interior to the neutrinosphere. Thus the neutrino luminosities are boosted and the neutrino heating behind the supernova shock is enhanced. The analysis by Bruenn & Dineva (1996) and more recently by Bruenn et al. (2004), however, has demonstrated that neutrino diffusion leads to lepton number equilibration between perturbed fluid elements and their surroundings that is faster than assumed by Wilson & Mayle (1993,1988). Therefore neutron fingers are unlikely to occur in the supernova core. Bruenn et al. (2004) instead discovered a new mode of doubly-diffusive instability, which they termed "lepto-entropy fingers'' and which is also associated with neutrino-mediated thermal and lepton diffusion. The importance of this phenomenon during the early, critical phases of the explosion, however, was recently questioned by Dessart et al. (2005) because of its slow growth compared to Ledoux convection. The latter, in turn, was predicted to play a role in supernovae on grounds of 1D models of the neutrino cooling phase of nascent neutron stars. A Ledoux-type of convection was indeed found to be present during the first second after neutron star formation in 2D hydrodynamic simulations by Keil (1997), Keil et al. (1996), Janka & Keil (1998) and Janka et al. (2001). The latter simulations, however, considered only the proto-neutron star without self-consistently following its feedback with the environment of the supernova core. Moreover, a grey, flux-limited equilibrium "ray-by-ray'' diffusion code for the neutrino transport was used, with strong simplifications in the description of the opacities.
Only recently multi-dimensional simulations of stellar core collapse and post-bounce evolution with a spectral treatment of the neutrino transport have become possible (Buras et al. 2003,2006; Livne et al. 2004; Walder et al. 2005; Swesty & Myra 2005a,b; Burrows et al. 2006). Although these current approaches are the first steps of removing the severe deficiencies of the previous generation of multi-dimensional models, all of them still contain approximations of various, and different, aspects in the treatment of 2D transport. Swesty & Myra (2005a,b), for example, use a flux-limited diffusion description, an approximation also made by Walder et al. (2005) and Dessart et al. (2005), who in addition solve the transport for all neutrino energy groups independently. In contrast, Buras et al. (2006) have developed a "ray-by-ray plus'' approximation based on a variable Eddington factor solver for the coupled set of neutrino moments equations and Boltzmann equation, including a full coupling of the energy bins by neutrino reactions and by Doppler and gravitational redshift effects.
The approximations employed by the different groups are diverse and might hamper a detailed quantitative comparison of the results in the near future, and might constrain such efforts to a purely qualitative level. Eventually it will be necessary to test and possibly replace the current approximations by a more rigorous solution of the transport problem in the five- or six-dimensional phase space and in a relativistic framework, once the corresponding codes have become available and the necessary substantial increase of computer power has happened (Cardall 2004; Cardall et al. 2005).
Here we present results obtained with the multi-dimensional
neutrino-hydrodynamics code MUDBATH, which is the
"ray-by-ray plus'' implementation of the PROMETHEUS/VERTEX
code described in detail in Buras et al. (2005, Paper I).
In continuation of our previous work (Buras et al. 2003,2006),
where also a broader introduction into the status of the field
and its open questions is provided, we present here 1D simulations for nine different progenitor stars with masses between 11.2![]() and 25
and 25![]() ,
and compare them
with 2D simulations for three of these stars.
The core collapse and post-bounce evolution of these models was
followed until nearly 300 ms after shock formation.
,
and compare them
with 2D simulations for three of these stars.
The core collapse and post-bounce evolution of these models was
followed until nearly 300 ms after shock formation.
Using a state-of-the-art treatment of spectral neutrino transport for hydrodynamical supernova simulations, the main goals of our work are:
We have chosen a total of nine progenitors from different groups doing
stellar evolution modeling. Details of the models can be found in
Appendix A. These models are listed there in
Table A.1 and cover a zero age main sequence
mass (ZAMS mass)
range from 11 to 25
![]() .
They represent various types of
pre-collapse stellar structures.
.
They represent various types of
pre-collapse stellar structures.
The one-dimensional core-collapse simulations were performed with our 1D
neutrino-hydrodynamics code VERTEX with spectral neutrino transport,
using spherical coordinates and the physics described in detail in
Buras et al. (2006). This includes a state-of-the-art treatment of
neutrino interactions and an approximative description of general
relativistic effects. The simulations described in the previous
and in the present paper were done with the equation of state (EoS)
of Lattimer & Swesty (1991), supplemented by a general lepton-photon-baryon
EoS (ideal gases with Coulomb corrections) that extends to
densities below those described by the Lattimer & Swesty
EoS![]() The numerical
resolution used for hydrodynamics and neutrino transport was also
specified in Buras et al. (2006).
The numerical
resolution used for hydrodynamics and neutrino transport was also
specified in Buras et al. (2006).
The evolution can be separated into the phases of collapse, bounce, prompt shock propagation, neutrino burst, and accretion phase, which is in some cases accompanied by a transient shock expansion. None of our 1D simulations yields a prompt or delayed explosion.
The phases of core collapse, shock formation and propagation, and
![]() burst at shock breakout reveal only
little differences between the progenitors
because the core structure and properties are very similar or become
very similar during collapse (for details, see Appendix B
and also Liebendörfer et al. 2002).
At the moment when the
burst at shock breakout reveal only
little differences between the progenitors
because the core structure and properties are very similar or become
very similar during collapse (for details, see Appendix B
and also Liebendörfer et al. 2002).
At the moment when the
![]() burst is
emitted the shock has reached an enclosed mass of
burst is
emitted the shock has reached an enclosed mass of ![]()
![]() outside of which differences in the progenitor structure become
larger. Therefore the mass infall rate through the shock begins to
differ between the models. At the same time the postshock velocities
become negative and the shock has converted to a stalled accretion
shock. Since the rate of mass accretion by the shock is very high
shortly after bounce, the shock is still pushed outward for
some time due to matter accumulating behind it. This "passive''
expansion of the shock comes to an end when the mass accretion
rate has dropped sufficiently and the neutrino cooling and
settling of the accreted matter withdraw support from the shock.
The conditions during this phase change only slowly. The situation
can therefore roughly be characterized by steady-state conditions
that depend on a number of parameters governing the accretion
phase, i.e. the mass accretion
rate through the shock,
outside of which differences in the progenitor structure become
larger. Therefore the mass infall rate through the shock begins to
differ between the models. At the same time the postshock velocities
become negative and the shock has converted to a stalled accretion
shock. Since the rate of mass accretion by the shock is very high
shortly after bounce, the shock is still pushed outward for
some time due to matter accumulating behind it. This "passive''
expansion of the shock comes to an end when the mass accretion
rate has dropped sufficiently and the neutrino cooling and
settling of the accreted matter withdraw support from the shock.
The conditions during this phase change only slowly. The situation
can therefore roughly be characterized by steady-state conditions
that depend on a number of parameters governing the accretion
phase, i.e. the mass accretion
rate through the shock,
![]() ,
the mass
,
the mass
![]() and radius
and radius
![]() of the proto-neutron star (PNS)
of the proto-neutron star (PNS)![]() ,
and the neutrino luminosity
,
and the neutrino luminosity ![]() (for a detailed discussion,
see Appendix B). In recent
analytic studies (Janka 2001; Arcones Segovia 2003) hydrostatic
solutions are discussed which fairly well describe the nearly
stationary accretion of the stalled shock as seen in the numerical
simulations at later post-bounce times,
provided that the model does not encounter quick changes such as a
sudden drop of
(for a detailed discussion,
see Appendix B). In recent
analytic studies (Janka 2001; Arcones Segovia 2003) hydrostatic
solutions are discussed which fairly well describe the nearly
stationary accretion of the stalled shock as seen in the numerical
simulations at later post-bounce times,
provided that the model does not encounter quick changes such as a
sudden drop of
![]() ,
or the onset of the explosion.
,
or the onset of the explosion.
All 1D models fail to explode and the shock retreats to <100 km
towards the end of our simulations (see top panel in Fig. B.4
in Appendix B). What is the effect of neutrino
heating behind the shock? To discuss this question we consider two
timescales, following Janka & Keil (1998), Janka et al. (2001),
and Thompson et al. (2005). The advection timescale of matter falling
inward from the shock to the gain radius is
While the advection timescale represents the time matter spends in the
gain layer (between shock and gain radius), the heating timescale
measures the time needed for neutrino heating to deposit an energy
equivalent to the binding energy of the matter. Clearly, heating is of
no importance as long as
![]() .
Thus, for obtaining a neutrino-driven explosion,
the condition
.
Thus, for obtaining a neutrino-driven explosion,
the condition
![]() must hold for
longer than a time interval
must hold for
longer than a time interval
![]() (see the discussion
in Janka & Keil 1998; Janka et al. 2001; Janka 2001;
and Thompson et al. 2005). Note
that this condition is not necessarily sufficient for an explosion but
it tells one when a visible shock expansion can be expected.
(see the discussion
in Janka & Keil 1998; Janka et al. 2001; Janka 2001;
and Thompson et al. 2005). Note
that this condition is not necessarily sufficient for an explosion but
it tells one when a visible shock expansion can be expected.
Looking at the timescales and their ratio (Figs. 1,
2), one recognizes that most models have long heating
timescales and thus neutrino heating is inefficient in causing
shock expansion. The ratio
![]() is always
less than 1/2 except in the two low-mass models, s11.2 and n13, where
neutrino heating is stronger during a short period of time.
is always
less than 1/2 except in the two low-mass models, s11.2 and n13, where
neutrino heating is stronger during a short period of time.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4654f080.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg104.gif) |
Figure 1: The advection timescales as defined in Eq. (1) versus post-bounce time. The lines are smoothed over time intervals of 5 ms. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4654f090.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg105.gif) |
Figure 2:
The timescale ratios,
|
| Open with DEXTER | |
The ratio becomes largest during the transient shock expansion
associated with the times when composition interfaces reach the
shock and the entropy makes a jump. This phenomenon, which is most
extreme at the edges of the small iron cores in
Model n13 at
![]() ms and in Model s11.2 around
ms and in Model s11.2 around
![]() ms, but in a weaker form is also present in
Models s1b, s20.0, and s15s7b2 at around
ms, but in a weaker form is also present in
Models s1b, s20.0, and s15s7b2 at around
![]() ms,
135 ms, and 170 ms, respectively, occurs because the density and
therefore the mass accretion rate of the infalling matter drops
at the interfaces of shells of different composition
(Appendix A). The sudden decrease of the ram pressure
allows for a transient shock expansion until the shock finds a new
equilibrium position at a larger radius.
ms,
135 ms, and 170 ms, respectively, occurs because the density and
therefore the mass accretion rate of the infalling matter drops
at the interfaces of shells of different composition
(Appendix A). The sudden decrease of the ram pressure
allows for a transient shock expansion until the shock finds a new
equilibrium position at a larger radius.
With a larger shock radius the postshock velocities are lower and the
advection timescale increases. More efficient neutrino heating further
strengthens the shock, the shock can therefore expand to even larger
radii. This behaviour is obtained in Model n13, and especially in
Model s11.2, where
![]() is close to
unity for a period of
about 20 ms. This, however, is shorter than the heating timescale
is close to
unity for a period of
about 20 ms. This, however, is shorter than the heating timescale
![]() ms. The pronounced growth of
the shock radius and of the advection timescale for Model s11.2, which
results in the large local maxima of the corresponding curves in
Figs. 1, 2, and B.4,
is produced by a continuous
strong decrease of the mass accretion rate, see Fig. B.4. After
113 ms post bounce this phase is over and the mass accretion rate
continues to decline less rapidly. The shock then retreats quickly and
finds a new quasi-stationary radius, where, however, neutrino heating
becomes less efficient again.
ms. The pronounced growth of
the shock radius and of the advection timescale for Model s11.2, which
results in the large local maxima of the corresponding curves in
Figs. 1, 2, and B.4,
is produced by a continuous
strong decrease of the mass accretion rate, see Fig. B.4. After
113 ms post bounce this phase is over and the mass accretion rate
continues to decline less rapidly. The shock then retreats quickly and
finds a new quasi-stationary radius, where, however, neutrino heating
becomes less efficient again.
In Models s15s7b2, s20.0, and s1b the drop of
![]() leads also to
shock expansion, but the effect is not strong enough to change
leads also to
shock expansion, but the effect is not strong enough to change
![]() significantly; also, in these models the
composition interface reaches the shock so late that the shock is already
deep in the gravitational potential well and the postshock velocities
are considerably higher than in Models n13 and s11.2. Therefore
significantly; also, in these models the
composition interface reaches the shock so late that the shock is already
deep in the gravitational potential well and the postshock velocities
are considerably higher than in Models n13 and s11.2. Therefore
![]() remains well below unity.
remains well below unity.
In summary, we find that all our 1D simulations evolve both
qualitatively and quantitatively in a similar way. In spite of maximum
shock radii around 130-150 km the models do not reveal
explosions. Only in the two lightest progenitor models, s11.2 and n13,
the drop in
![]() at the composition shell interfaces is
sufficiently steep and large and happens sufficiently early to allow
the shocks to reach a radius of 170 km. Nevertheless, the models are
far from producing explosions because the advection timescales remain
always shorter than the timescales for neutrino heating, and the
phases where the ratio of both approaches unity are much shorter than
the heating timescale itself. Therefore neutrino heating is not strong
enough to drive an explosion.
at the composition shell interfaces is
sufficiently steep and large and happens sufficiently early to allow
the shocks to reach a radius of 170 km. Nevertheless, the models are
far from producing explosions because the advection timescales remain
always shorter than the timescales for neutrino heating, and the
phases where the ratio of both approaches unity are much shorter than
the heating timescale itself. Therefore neutrino heating is not strong
enough to drive an explosion.
Table 1:
Parameters of computed 2D models for progenitor stars with different
masses.
![]() is the angular velocity of the Fe-core,
which is assumed to rotate uniformly, prior to collapse,
is the angular velocity of the Fe-core,
which is assumed to rotate uniformly, prior to collapse, ![]() and
and
![]() are the polar angles of the lateral grid boundaries, and
are the polar angles of the lateral grid boundaries, and
![]() is the number of grid points in the lateral
direction.
is the number of grid points in the lateral
direction.
![]() denotes the time (relative to the bounce
time) when the simulation was started or continued in 2D.
denotes the time (relative to the bounce
time) when the simulation was started or continued in 2D.
The one-dimensional models analyzed so far have one significant
shortcoming: they do not take into account hydrodynamic instabilities
in the stellar core. Convection, especially the so-called hot bubble (HB)
convection in the gain layer, has been seen to strengthen the shock in
previous multi-dimensional supernova simulations.
We can analyze our 1D models for the existence of
Ledoux-unstable regions. For this purpose we introduce the new
variable (defined as parameter ![]() in Foglizzo et al. 2005),
in Foglizzo et al. 2005),
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4654f110.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg133.gif) |
Figure 3:
Number of e-foldings that the amplitude of perturbations
is estimated to grow during advection of the flow from the shock to
the gain radius in our 1D models (cf. Eq. (4)).
The lines are smoothed over time
intervals of 5 ms. For Model n13,
|
| Open with DEXTER | |
For our two-dimensional studies with assumed azimuthal symmetry we
used the numerical code, input physics, and resolution as described in
Buras et al. (2006) and specified in Table 1. The innermost
core of 1.7 km radius was computed in spherical symmetry.
We have chosen three representative progenitors: s11.2, which shows
favorable conditions for developing strong Ledoux convection in the
neutrino-heated postshock layer, as well
as the two less promising progenitors, s15s7b2 and s20.0. A total of
seven simulations were performed in 2D, see
Table 1. Most simulations were started from a 1D model around 7 ms after bounce, at which time the radial velocity was
randomly perturbed with an amplitude of ![]() 1%. For each progenitor
we calculated a model with low angular resolution (
1%. For each progenitor
we calculated a model with low angular resolution (
![]() )
with a
)
with a
![]() lateral wedge around the equatorial plane of the polar grid.
In addition, we
calculated high-resolution (
lateral wedge around the equatorial plane of the polar grid.
In addition, we
calculated high-resolution (
![]() )
versions for the two lighter
progenitors s11.2 and s15s7b2. The corresponding 15
)
versions for the two lighter
progenitors s11.2 and s15s7b2. The corresponding 15![]() 2D
simulation was started at
the onset of core collapse with an initial random density perturbation
(in Model s15_64_p) of
2D
simulation was started at
the onset of core collapse with an initial random density perturbation
(in Model s15_64_p) of ![]() 2%
in order to address the question whether
the onset of convection after bounce changes
when nonradial perturbations in the stellar core are followed
through infall instead of being imposed shortly after bounce on a
1D collapse model in mapping the latter onto a 2D grid.
Another simulation for the
2%
in order to address the question whether
the onset of convection after bounce changes
when nonradial perturbations in the stellar core are followed
through infall instead of being imposed shortly after bounce on a
1D collapse model in mapping the latter onto a 2D grid.
Another simulation for the
![]() progenitor, Model s112_128_f, with a resolution of
progenitor, Model s112_128_f, with a resolution of
![]() ,
was
performed with a full
,
was
performed with a full
![]() grid. Finally, one simulation with
the 15
grid. Finally, one simulation with
the 15
![]() progenitor, Model s15_64_r, included rotation. The
angular frequency at the onset of core collapse was assumed to be
progenitor, Model s15_64_r, included rotation. The
angular frequency at the onset of core collapse was assumed to be
![]() and constant in the Fe and Si core, and decreasing (spherically symmetrically) like r-3/2 outside of 1750 km (1.43
and constant in the Fe and Si core, and decreasing (spherically symmetrically) like r-3/2 outside of 1750 km (1.43
![]() ). This choice of the
rotation rate and rotational profile was motivated by results for
pre-collapse stellar cores of stars whose evolution is followed
including the angular momentum transport by magnetic fields
(Heger et al. 2005). Our choice of
). This choice of the
rotation rate and rotational profile was motivated by results for
pre-collapse stellar cores of stars whose evolution is followed
including the angular momentum transport by magnetic fields
(Heger et al. 2005). Our choice of
![]() in the
iron core is roughly ten times lower than the core rotation of
non-magnetic stars (Woosley et al. 2002) and about ten times larger
than Heger et al.'s rotation rates of magnetized stars. It
intends to maximize the effects of rotation during core
collapse under the constraints
that (a) the initial star can well be considered as spherically symmetric,
and that (b) the assumed rotation, which is superimposed on a 1D stellar model, does not imply significant deviations from the
hydrostatic equilibrium and gravitationally bound state of the
progenitor model.
In order to fulfill both requirements we limit the rate of
rotation such that the influence of centrifugal forces is
very small prior to collapse:
in the
iron core is roughly ten times lower than the core rotation of
non-magnetic stars (Woosley et al. 2002) and about ten times larger
than Heger et al.'s rotation rates of magnetized stars. It
intends to maximize the effects of rotation during core
collapse under the constraints
that (a) the initial star can well be considered as spherically symmetric,
and that (b) the assumed rotation, which is superimposed on a 1D stellar model, does not imply significant deviations from the
hydrostatic equilibrium and gravitationally bound state of the
progenitor model.
In order to fulfill both requirements we limit the rate of
rotation such that the influence of centrifugal forces is
very small prior to collapse:
![]() everywhere for the initial ratio
of the centrifugal force to the gravitational force. The density of the
stellar model was perturbed by
everywhere for the initial ratio
of the centrifugal force to the gravitational force. The density of the
stellar model was perturbed by ![]() 1% and the simulation was carried out
with a lateral resolution of
1% and the simulation was carried out
with a lateral resolution of
![]() in a wedge from the polar
axis to the equator (i.e. besides axial symmetry also equatorial
symmetry was assumed).
in a wedge from the polar
axis to the equator (i.e. besides axial symmetry also equatorial
symmetry was assumed).
In Sect. 3.1 we shall focus on convection below the
neutrinosphere of the proto-neutron star ("PNS convection''). We will
try to classify this convection and will describe its effects on the
evolution of the supernova and on the neutrino emission. To this end
we will develop a mixing algorithm as described in Appendix D and will present a 1D simulation performed with
it. We shall finish by discussing resolution and perturbation effects
and differences between the simulations with different progenitors. In
Sect. 3.2 a description of convective overturn in the
neutrino-heating layer behind the shock ("hot bubble (HB)
convection'') will follow. Again, we will first discuss differences
compared to 1D models. Here, the resolution and size of the angular
wedge play a much more important role and we need to elaborate on both
aspects. Also the sensitivity of the onset of HB convection to the
size of the seed perturbations will be discussed, and our results
for the evolution of pre-collapse perturbations during the infall phase
in Model s15_64_p can be found in Appendix E.
Since differences of this model compared to Model s15_32 were
minor, the results of this simulation will be included
in the plots following below mostly without any special discussion.
In Sect. 3.3 we shall describe our calculation with the
full
![]() grid, which allows low (l=1,2) modes to develop with
important consequences. Section 3.4 will contain our
results for the rotating
grid, which allows low (l=1,2) modes to develop with
important consequences. Section 3.4 will contain our
results for the rotating
![]() model. We shall discuss the
influence of rotation on the PNS, its neutrino emission, and
convection according to the Solberg-Høiland-criterion (generalized
to include the effects of
model. We shall discuss the
influence of rotation on the PNS, its neutrino emission, and
convection according to the Solberg-Høiland-criterion (generalized
to include the effects of
![]() -gradients on convection). The role of
centrifugal forces for the HB convection and shock propagation will
also be addressed.
-gradients on convection). The role of
centrifugal forces for the HB convection and shock propagation will
also be addressed.
Many phenomena inside the PNS, e.g. the conditions for convection in its interior, can mostly be discussed without taking into account the convective activity in the HB layer (but not inversely!). For several of the discussed models (s15_32, s20_32, s15_64_p) this is true, because they develop only weak HB convection with little impact on the shock propagation and on the PNS. Therefore nearly steady-state conditions prevail around the PNS, the mass in the gain layer changes only very slowly, and the mass accretion rate onto the PNS is approximately the same as the mass accretion rate through the shock. Moreover, the accretion flow onto the PNS is nearly laminar and isotropic.
In order to analyze the hydrostatic neutron star for convective
instability we consider the Brunt-Väisälä frequency,
Eq. (5). However, since neutrinos are strongly coupled
with the dense plasma and close to equilibrium with the matter in the PNS,
we generalize the Ledoux-criterion to a "Quasi-Ledoux criterion'', in
which the effects of neutrino transport are approximately accounted for
(see Wilson & Mayle 1993; Buras et al. 2006),
Recently, Bruenn et al. (2004) presented an elaborate discussion of hydrodynamic instabilities in the PNS including the effects of neutrino diffusion (an extension of a previous analysis by Bruenn & Dineva 1996). They argue that local perturbations in the lepton number will be reflected in the neutrino phase space and thus cause a net neutrino diffusion which tries to wash out the perturbations, an effect which can be accounted for by a "response function''. Since neutrinos also carry entropy, the neutrino diffusion that smoothes the lepton number perturbations will create entropy perturbations. This effect is characterized by a "cross response function''. Of course, entropy perturbations will in an analogous way induce an equilibrating net neutrino diffusion which at the same time transports lepton number between the fluid elements and their surroundings, corresponding to another "response function'' and a "cross response function''. Bruenn et al. (2004) found in a numerical analysis that perturbation-induced neutrino lepton number transport by diffusion is considerably more rapid than thermal transport, and that the transport of lepton number reacts faster to entropy perturbations than to lepton number perturbations. For such a situation convective instability should set in for most stellar conditions, even when the fluid is Ledoux stable. In particular, Bruenn et al. (2004) describe two kinds of instabilities in the presence of neutrino diffusion: one instability occurs when the entropy difference between a displaced fluid element and its surroundings in a background with an entropy gradient results in a lepton fraction difference, which provides a driving force such that the induced perturbation grows. The buoyant rise of a perturbed fluid element, together with neutrino diffusion, will thus further increase the difference in entropy between the fluid elements and their surroundings and will create lepton number fluctuations from entropy perturbations, which continue to drive buoyant motion. A second instability exists where the neutrino diffusion creates an "overstable'' situation, i.e. where the effect of neutrino diffusion will drive a perturbed fluid element back to its original position, but to such an extent that the fluid element overshoots and thus oscillates around its original position with increasing amplitude. Bruenn et al. (2004) call these two doubly-diffusive instabilities "lepto-entropy finger'' (LEF) convection and "lepto-entropy semiconvection'' (LESC), respectively. They also distinguish Ledoux convection. However, Ledoux and LEF convection are closely related (LEF convection is an extension of Ledoux convection).
Bruenn et al.'s analysis of stellar profiles shows that Ledoux/LEF
convection should appear in an extended region of the PNS from around
15 km to the neutrinospheres, whereas LESC should be visible deeper in
the core. We suppose that our stellar profiles might yield
qualitatively similar results if one applied their analysis. Our
two-dimensional simulations, however, do not confirm their predictions
in detail. For example, Model s15_32 shows convective instability
between 17 km and 30 km at
![]() ms, see
Fig. 5a.
We interpret this as Ledoux convection and determine growth
rates of the Ledoux instability (cf. Figs. 6
and 9) that are typically more than a
factor of 10 higher than those of LEF found by Bruenn et al. (2004).
Our hydrodynamic simulations reveal a behavior in agreement with
our larger rate estimates. Moreover,
the region showing convective activity does not extend to the
neutrinospheres, which are beyond 60 km at that time
(Fig. 11), and also at later times the upper boundary
of the convective layer stays well below the neutrinospheres
(Fig. 5b).
ms, see
Fig. 5a.
We interpret this as Ledoux convection and determine growth
rates of the Ledoux instability (cf. Figs. 6
and 9) that are typically more than a
factor of 10 higher than those of LEF found by Bruenn et al. (2004).
Our hydrodynamic simulations reveal a behavior in agreement with
our larger rate estimates. Moreover,
the region showing convective activity does not extend to the
neutrinospheres, which are beyond 60 km at that time
(Fig. 11), and also at later times the upper boundary
of the convective layer stays well below the neutrinospheres
(Fig. 5b).
We suspect that the discussion
by Bruenn et al. (2004) is not fully applicable up to the neutrinospheres.
It is based on the assumptions that
the mean free path (mfp) of neutrinos is much smaller than the
size of the displaced fluid elements and shorter than local gradients
in the background medium so that neutrinos diffuse and stay close to
local equilibrium. In contrast, Fig. 4 reveals that
the neutrino mfp becomes large near the upper edge of the convective
zone, in particular for muon and tau neutrinos.
As a consequence, the neutrinos start streaming increasingly
rapidly and the neutrino densities in this region (first for ![]() and
and ![]() ,
then for
,
then for
![]() and finally
for
and finally
for
![]() )
begin to deviate from local chemical
equilibrium. The net rate of neutrino losses therefore grows
strongly, leading to a quick rise of the neutrino
luminosities. Despite their growing mfp, the production of neutrinos
in the stellar medium is sufficiently strong to allow
for efficient energy and lepton number drain. We therefore
suspect that in the semitransparent layer below the
neutrinosphere the accelerating radial transport causes enhanced
neutrino release such that entropy and lepton number fluctuations
are wiped out by neutrinos streaming off. This happens before local
exchange between fluid elements and their surroundings can efficiently
take place as assumed by Bruenn et al. (2004). LEF instabilities thus have
no time to grow.
)
begin to deviate from local chemical
equilibrium. The net rate of neutrino losses therefore grows
strongly, leading to a quick rise of the neutrino
luminosities. Despite their growing mfp, the production of neutrinos
in the stellar medium is sufficiently strong to allow
for efficient energy and lepton number drain. We therefore
suspect that in the semitransparent layer below the
neutrinosphere the accelerating radial transport causes enhanced
neutrino release such that entropy and lepton number fluctuations
are wiped out by neutrinos streaming off. This happens before local
exchange between fluid elements and their surroundings can efficiently
take place as assumed by Bruenn et al. (2004). LEF instabilities thus have
no time to grow.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4654f10x.eps}
\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg156.gif) |
Figure 4:
Top: transport mean free paths of muon and tau neutrinos
and antineutrinos for different energies as functions of radius at 243 ms after bounce, about 200 ms after the onset of PNS
convection in Model s15_32. Also shown is the local density scale
height (bold solid line). The vertical line marks the radius of the
outer edge of the convective layer in the PNS
(cf. Fig. 5).
Bottom: mean free paths of
|
| Open with DEXTER | |
![\begin{figure}
\par\begin{tabular}{lr}
\put(0.9,0.3){{\Large\bf a}}
\includegr...
...e\bf d}}
\includegraphics[width=8.5cm]{4654f13d.eps} \end{tabular} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg157.gif) |
Figure 5:
Snapshots of PNS convection in Model s15_32 at 48 ms a)
and 243 ms b) after bounce. The upper left quadrants of each plot depict
color-coded the absolute value of the matter velocity, the other
three quadrants show for
|
| Open with DEXTER | |
LESC as predicted by Bruenn et al. (2004) to occur far inside the PNS is not visible in our models. However, these authors mention that the existence of LESC is very sensitive to the exact values of the response functions, which in turn depend on the details of the neutrino interactions. We suspect that the different description of neutrino-matter interactions in our simulations might prevent LESC. In any case, convection very far inside the PNS should have less influence on the shock dynamics than the PNS convection which we see in our models. Therefore we will ignore the possibility of LESC in the following discussion and consider its effects on the neutrino emission and the explosion mechanism as negligible.
In Figs. 6-8, we see that
a convectively unstable layer begins to develop in the PNS about 30 ms
after bounce. This happens in a
region which initially is stable due to a positive entropy gradient,
see Fig. 7. As neutrino diffusion carries entropy
away more efficiently at larger radii where the optical depth is lower,
the entropy profile flattens, and finally the entropy gradient turns
negative and the PNS becomes Ledoux unstable. Ten ms later the
perturbations have grown (with a growth rate of about
![]() ,
see
Figs. 6 and 9) to become non-linear
and strong PNS convection has set in. This can be seen in the large lateral
velocities in Fig. 8 (dark shaded). Similar to
Keil (1997), we find that the structure of the convective cells is
initially that of rolls with angular sizes between 20
,
see
Figs. 6 and 9) to become non-linear
and strong PNS convection has set in. This can be seen in the large lateral
velocities in Fig. 8 (dark shaded). Similar to
Keil (1997), we find that the structure of the convective cells is
initially that of rolls with angular sizes between 20
![]() and 30
and 30
![]() and radial extension between 10 and 15 km
(Fig. 5a). The rolls are stable for about 5 ms,
then decay and form again at different locations in the same
layer. 200 ms later, the contraction of the PNS has reduced the radial
size of the convective cells to 10 km. The overturn velocities are
around
and radial extension between 10 and 15 km
(Fig. 5a). The rolls are stable for about 5 ms,
then decay and form again at different locations in the same
layer. 200 ms later, the contraction of the PNS has reduced the radial
size of the convective cells to 10 km. The overturn velocities are
around
![]() with peaks of up to
with peaks of up to
![]() .
At
later times the velocities decrease to values around
.
At
later times the velocities decrease to values around
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4654f150.eps}
\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg162.gif) |
Figure 6: Brunt-Väisälä frequency (Eq. (5)), using Eq. (7) as stability criterion, evaluated for different 1D models at 20, 30, and 40 ms after bounce. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4654f170.eps}
\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg163.gif) |
Figure 7: Lepton number and total entropy versus enclosed mass in the PNS for the 1D model s15s7b2 for different post-bounce times before the onset of PNS convection in the corresponding 2D simulation. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4654f160.eps}
\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg166.gif) |
Figure 8:
Convective region in Model s15_32. The dark-shaded regions have
lateral velocities above
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4654f180.eps}
\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg167.gif) |
Figure 9: Brunt-Väisälä frequency in the 1D simulation of the stellar progenitor s15s7b2 (thin) and the corresponding 2D simulation, Model s15_32 (thick), at 30 ms (dashed), 62 ms (solid), and 200 ms (dash-dotted) post-bounce. At 30 ms, the thin and thick dashed lines coincide. All lines are truncated at 50 km. Positive values indicate instability. For the 2D model the evaluation was performed with laterally averaged quantities. |
| Open with DEXTER | |
The region with large lateral velocities (>700 km s-1, dark shaded in Fig. 8) is wider than the layer with instability according to Eq. (7). This has two reasons: First, rising or sinking fluid elements can over- and undershoot into the adjacent stable layers. Second, the periodic boundary conditions applied in some of our simulations allow rings of uniform, lateral velocity to occur. This artificial phenomenon is associated with matter that settles from the neutrino-heated convective postshock layer onto the PNS and has obtained large lateral velocity components by participating in the overturn motion in the gain layer. The rings show up in Fig. 8 as a layer with high lateral velocities that moves from the "hot-bubble'' (HB) convective zone to the convection zone in the PNS between 100 and 150 ms post-bounce. Looking at the velocity distribution in 2D snapshots of the simulation, Fig. 5b, the rings can be identified around r=30 km.
Throughout our simulations, PNS convection occurs exterior to an
enclosed mass of
![]()
![]() , see Fig. 8. This inner boundary changes
only little during the simulations, whereas the
outer boundary of the convective layer moves outward in mass as time
goes on, following the ongoing accretion of matter on the PNS.
Keil et al. (1996) found in their
models that PNS convection develops in an initially narrow layer, but
the inner edge of this layer moves continuously deeper into the PNS.
Their models, however, were evolved until 1.3 s after bounce,
and the inward motion of the lower boundary of the
convective zone may take place at times not covered by our present
calculations. Moreover, the velocity at which the convective layer
digs deeper into the PNS must be expected to depend on the
treatment of the neutrino transport, which was described very
approximatively by grey, radial, flux-limited equilibrium diffusion
by Keil et al. (1996) and Keil (1997), who also made quite radical
approximations for the
neutrino-matter interactions (see Appendix in Keil & Janka 1995).
, see Fig. 8. This inner boundary changes
only little during the simulations, whereas the
outer boundary of the convective layer moves outward in mass as time
goes on, following the ongoing accretion of matter on the PNS.
Keil et al. (1996) found in their
models that PNS convection develops in an initially narrow layer, but
the inner edge of this layer moves continuously deeper into the PNS.
Their models, however, were evolved until 1.3 s after bounce,
and the inward motion of the lower boundary of the
convective zone may take place at times not covered by our present
calculations. Moreover, the velocity at which the convective layer
digs deeper into the PNS must be expected to depend on the
treatment of the neutrino transport, which was described very
approximatively by grey, radial, flux-limited equilibrium diffusion
by Keil et al. (1996) and Keil (1997), who also made quite radical
approximations for the
neutrino-matter interactions (see Appendix in Keil & Janka 1995).
We note here that a closer discussion of the first 200-300 ms
of post-bounce evolution, comparing these older diffusion simulations
with our present models, is not useful to convey our understanding
particularly of the
possible deficiencies of the simpler diffusion treatment. Such a
comparison is hampered by other very important differences between the
simulations. Firstly, the post-collapse models from which the calculations
of Keil et al. (1996) and Keil (1997) were started, were provided by
Bruenn and thus were computed with a neutrino transport treatment
that was not compatible with the one used for the subsequent 2D evolution. This must be suspected to have caused transient effects
during an early phase of the post-bounce evolution of undetermined
length. Such transients are not present in our current, consistent
models. Secondly, the simulations by Keil et al. (1996) and Keil (1997)
considered a neutron star of 1.1-1.2![]() and thus much smaller
in mass than the compact remnants of the models in this paper, which
grow in mass particularly rapidly during the first hundreds of
milliseconds after bounce when the mass accretion rates are still
high (see Fig. B.4).
And thirdly, neglecting the accretion layer outside of the neutron
star and placing the outer grid boundary near the neutrinosphere by
Keil et al. (1996) and Keil (1997) may also have caused differences of their
results from the present, full simulations of the collapsing supernova
core. We therefore refrain from attempting a closer comparison of these
old and our new models beyond the level of qualitative statements about the
existence, long-lasting presence, and basic structural features of a
convective layer inside the nascent neutron star.
and thus much smaller
in mass than the compact remnants of the models in this paper, which
grow in mass particularly rapidly during the first hundreds of
milliseconds after bounce when the mass accretion rates are still
high (see Fig. B.4).
And thirdly, neglecting the accretion layer outside of the neutron
star and placing the outer grid boundary near the neutrinosphere by
Keil et al. (1996) and Keil (1997) may also have caused differences of their
results from the present, full simulations of the collapsing supernova
core. We therefore refrain from attempting a closer comparison of these
old and our new models beyond the level of qualitative statements about the
existence, long-lasting presence, and basic structural features of a
convective layer inside the nascent neutron star.
The convective flow transports energy and lepton number from deeper
layers of the PNS closer to the neutrinospheres, thereby flattening
the entropy gradient and the lepton number profile, see
Fig. 10. However, at the end of the calculation the
initially quite steep negative
![]() gradient has not disappeared
completely. This suggests that the convective mass motions can not
efficiently transport lepton number over large distances. The
reason for this is the fact that
buoyant mass elements exchange leptons easily with their local
surroundings via neutrino diffusion. Therefore rising bubbles with
initially large
gradient has not disappeared
completely. This suggests that the convective mass motions can not
efficiently transport lepton number over large distances. The
reason for this is the fact that
buoyant mass elements exchange leptons easily with their local
surroundings via neutrino diffusion. Therefore rising bubbles with
initially large
![]() end up with low
end up with low
![]() when they reach the
outer stable layers of the PNS. For this to happen the timescale of
when they reach the
outer stable layers of the PNS. For this to happen the timescale of
![]() -equilibration between buoyant bubbles and their surroundings
via neutrino diffusion must be of the same order as the rise timescale
of the bubbles. This situation corresponds to a value of
-equilibration between buoyant bubbles and their surroundings
via neutrino diffusion must be of the same order as the rise timescale
of the bubbles. This situation corresponds to a value of
![]() in Eq. (7) close
to unity. If the rise time were much longer, the 1D and 2D profiles of
in Eq. (7) close
to unity. If the rise time were much longer, the 1D and 2D profiles of
![]() in the convective region would not differ, while if it were
much shorter, the
in the convective region would not differ, while if it were
much shorter, the
![]() profile would be flat like the entropy profile.
profile would be flat like the entropy profile.
A second effect contributes in establishing the observed conditions in
the convective PNS layer. In contrast to the energy loss from the
stellar medium, which is small in the considered period of time
compared to the huge heat capacity of
the accretion layer, lepton number is radiated away very
efficiently, at least initially. At early times, when
![]() is still
large in the convective PNS layer, the number flux of
is still
large in the convective PNS layer, the number flux of
![]() is much
larger than that of
is much
larger than that of
![]() and the lepton number loss proceeds very
rapidly. At later times, however, it slows down because
and the lepton number loss proceeds very
rapidly. At later times, however, it slows down because
![]() has
decreased and the release of
has
decreased and the release of
![]() and
and
![]() has become more similar.
has become more similar.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4654f190.eps}
\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg170.gif) |
Figure 10: Lepton number, total entropy, specific internal energy, and density profiles versus enclosed mass in the PNS for a sample of 1D (dotted) and 2D simulations of different progenitor stars, 200 ms after bounce (i.e., approximately 160 ms after the onset of PNS convection). For the 2D models angle-averaged quantities are plotted. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f200.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg171.gif) |
Figure 11: Radius of the electron neutrinosphere (as a measure of the PNS radius) for the 2D models and their corresponding 1D models. For Model s15_64_r we show the equatorial ( upper) and polar ( lower) neutrinospheric radii. For other 2D models, angle-averaged quantities are plotted. |
| Open with DEXTER | |
The redistribution of lepton number and energy gradually affects the
structure of the PNS. The "drain'' region, where
![]() and internal
energy
and internal
energy
![]() are extracted, has densities close to the
nuclear density (
are extracted, has densities close to the
nuclear density (
![]() ), whereas the "dump''
region, where lepton number and energy are deposited, has lower
densities (
), whereas the "dump''
region, where lepton number and energy are deposited, has lower
densities (
![]() ), see Fig. 8.
A detailed analysis presented in
Appendix C reveals that the transport of lepton number
from the drain region to the dump region will effectively lead to
expansion. Also the transfer of energy from the drain region to the
dump layer leads to an expansion of the PNS. Consequently the
neutrinosphere radii in 2D simulations are larger than in the
corresponding 1D models, see Fig. 11.
), see Fig. 8.
A detailed analysis presented in
Appendix C reveals that the transport of lepton number
from the drain region to the dump region will effectively lead to
expansion. Also the transfer of energy from the drain region to the
dump layer leads to an expansion of the PNS. Consequently the
neutrinosphere radii in 2D simulations are larger than in the
corresponding 1D models, see Fig. 11.
The changes in the radial profiles of energy and lepton number and the expansion of the PNS relative to 1D simulations have interesting consequences for the neutrino emission. Convection in the PNS alters the emission of neutrinos in and above the dump region and therefore the PNS loses energy and lepton number at a different rate than without convection. In this case the linear analysis (Appendix C) shows that an increased loss of lepton number in and above the dump region leads to a more extended PNS, while an increased loss of energy leads to a more compact PNS (Fig. C.1). As will be discussed in detail below, PNS convection causes enhanced lepton number release and initially reduced energy loss via neutrinos, both supporting the "expansion'' of the PNS relative to the 1D simulations. At times later than 150 ms post bounce, the energy loss in neutrinos is also enhanced relative to the 1D models, without however being able to compensate the inflative effects on the PNS structure caused by the convective redistribution of energy and lepton number and by the enhanced lepton losses form the neutrinospheric layer due to neutrino emission.
Immediately after the onset of PNS convection the increase of
![]() near the upper boundary of the convective region leads to a higher
electron chemical potential
near the upper boundary of the convective region leads to a higher
electron chemical potential
![]() and therefore a higher
electron neutrino chemical potential
and therefore a higher
electron neutrino chemical potential
![]() .
Thus the
.
Thus the
![]() abundance (given
by equilibrium conditions) decreases significantly in this
layer. Although this happens in a region where the
abundance (given
by equilibrium conditions) decreases significantly in this
layer. Although this happens in a region where the
![]() luminosity has reached only 5-10% of its final value (see
Fig. 5a) the decrease is sufficiently large to
lower the total
luminosity has reached only 5-10% of its final value (see
Fig. 5a) the decrease is sufficiently large to
lower the total
![]() luminosity by several percent. When the PNS
convection has developed to full power,
luminosity by several percent. When the PNS
convection has developed to full power,
![]() can be lowered by
up to 10% in comparison to the 1D models, see
Fig. 12. The decrease of the
can be lowered by
up to 10% in comparison to the 1D models, see
Fig. 12. The decrease of the
![]() equilibrium
abundance also affects the heavy-lepton ("
equilibrium
abundance also affects the heavy-lepton ("![]() '' for
'' for ![]() ,
,
![]() ,
,
![]() ,
or
,
or
![]() )
luminosity via the process
)
luminosity via the process
![]() ,
which is the
dominant
,
which is the
dominant ![]() production process in the region where the reduction of
the
production process in the region where the reduction of
the
![]() abundance happens. However,
abundance happens. However,
![]() in that region has
already attained 70% of its final value, and therefore
the reduced
in that region has
already attained 70% of its final value, and therefore
the reduced ![]() production rate leads to a decrease of the
radiated
production rate leads to a decrease of the
radiated ![]() luminosity by at most 5%, typically less
(Fig. 12).
luminosity by at most 5%, typically less
(Fig. 12).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f210.eps}
\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg182.gif) |
Figure 12:
Luminosities of electron neutrinos,
|
| Open with DEXTER | |
After 100 ms post-bounce these moderate effects are overridden by the
structural changes of the PNS, which lead to larger neutrinospheric
radii than in 1D models, as well as the ongoing convective transport
of energy into the region below the ![]() -sphere. Moreover, the
convective layer now extends to lower densities so that the region
affected by PNS convection contributes now 30%, 30%, and 90% to the
radiated
-sphere. Moreover, the
convective layer now extends to lower densities so that the region
affected by PNS convection contributes now 30%, 30%, and 90% to the
radiated
![]() ,
,
![]() ,
and
,
and ![]() luminosities, respectively (see
Fig. 5b), although this region has a
transport optical
depth (for a definition see Buras et al. 2006, Eq. (28)) in excess of 40, 14, and 10 for
luminosities, respectively (see
Fig. 5b), although this region has a
transport optical
depth (for a definition see Buras et al. 2006, Eq. (28)) in excess of 40, 14, and 10 for
![]() ,
,
![]() ,
and
,
and ![]() ,
respectively, and
therefore is still well inside the neutrinosphere.
,
respectively, and
therefore is still well inside the neutrinosphere.
Larger neutrinospheric radii without the described
convective inflow of energy would lead to lower luminosities as a
consequence of an associated decrease of the neutrinospheric
temperature ![]() .
This, for example, is seen in simulations with
different EoSs where the PNS radius depends on the high-density EoS
properties. A larger PNS radius correlates with lower luminosities
(Janka et al. 2005).
In contrast, in our 2D models the luminosities
increase. We indeed find lower
.
This, for example, is seen in simulations with
different EoSs where the PNS radius depends on the high-density EoS
properties. A larger PNS radius correlates with lower luminosities
(Janka et al. 2005).
In contrast, in our 2D models the luminosities
increase. We indeed find lower ![]() ,
which result in lower mean
neutrino energies
,
which result in lower mean
neutrino energies
![]() (defined by the ratio of
energy to number flux), see
Fig. 13. The difference can be up to 10% for all
neutrino kinds after 200 ms of PNS convection. Because of the energy
transport to the neutrinospheres by convection, however, this
reduction in
(defined by the ratio of
energy to number flux), see
Fig. 13. The difference can be up to 10% for all
neutrino kinds after 200 ms of PNS convection. Because of the energy
transport to the neutrinospheres by convection, however, this
reduction in ![]() is much weaker than it would be in an
adiabatically expanding layer. Apparently, the larger neutrinospheric
radii and only slightly lower temperatures lead to a net increase of
the luminosities relative to the 1D results, see
Fig. 12. The effect is strongest for
is much weaker than it would be in an
adiabatically expanding layer. Apparently, the larger neutrinospheric
radii and only slightly lower temperatures lead to a net increase of
the luminosities relative to the 1D results, see
Fig. 12. The effect is strongest for ![]() ,
which
decouple energetically from the medium already near the upper boundary
of the convective layer (Fig. 5b);
after 200 ms of convection,
,
which
decouple energetically from the medium already near the upper boundary
of the convective layer (Fig. 5b);
after 200 ms of convection,
![]() is
almost 20% higher than in the 1D models.
is
almost 20% higher than in the 1D models.
![]() increases only by
a few percent, while
increases only by
a few percent, while
![]() is almost identical in 1D and 2D
models, which means that the higher electron chemical potentials
and the effects associated with the convective energy transport
and structural changes of the PNS nearly compensate each other.
is almost identical in 1D and 2D
models, which means that the higher electron chemical potentials
and the effects associated with the convective energy transport
and structural changes of the PNS nearly compensate each other.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f220.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg186.gif) |
Figure 13: Average energies of the radiated neutrinos (defined by the ratio of energy to number flux) for the 2D models and for the corresponding 1D models, evaluated at a radius of 400 km for an observer at rest. The lines are smoothed over time intervals of 5 ms. Note that the average neutrino energies of Model s15_32 were corrected for the differences arising from the slightly different effective relativistic gravitational potential as described in the context of Table 1. |
| Open with DEXTER | |
After the onset of PNS convection the 2D models deleptonize
faster than their 1D counterparts (Fig. 14).
The lepton number loss is enhanced after 250 ms of post-bounce
evolution by typically 8-10% (compare Fig. 14 with
Fig. B.5). The evolution of the total energy loss is
more complex and is smaller than in the 1D simulations for the first
![]() 100-140 ms of reduced energy emission.
Only afterwards the losses become stronger in the 2D cases.
However, even 250 ms after
bounce, the total energy loss is only 2-4% higher with PNS
convection.
100-140 ms of reduced energy emission.
Only afterwards the losses become stronger in the 2D cases.
However, even 250 ms after
bounce, the total energy loss is only 2-4% higher with PNS
convection.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{4654f230.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg187.gif) |
Figure 14:
Differences between the total lepton number ( top) and
energy losses ( bottom) of the 2D models and their corresponding 1D models as functions of post-bounce time. Here, |
| Open with DEXTER | |
Note that the neutrinospheric luminosities in 2D models relative to 1D models are increased by 25%, 15%, and 25% for
![]() ,
,
![]() ,
and
,
and ![]() after 200 ms. The effect of the PNS convection therefore
manifests itself more strongly at the neutrinospheres than farther
outside, because the luminosity differences get reduced due to
structural differences above the neutrinospheres and thus resulting
differences in the neutrino absorption and emission outside of the
neutrinospheres.
after 200 ms. The effect of the PNS convection therefore
manifests itself more strongly at the neutrinospheres than farther
outside, because the luminosity differences get reduced due to
structural differences above the neutrinospheres and thus resulting
differences in the neutrino absorption and emission outside of the
neutrinospheres.
We have performed several 2D simulations with varied resolution
(2.7
![]() and 1.35
and 1.35
![]() or 1.41
or 1.41
![]() )
and different choices of
the lateral grid (either a wedge with
)
and different choices of
the lateral grid (either a wedge with
![]() around the equator
or a full 180
around the equator
or a full 180
![]() grid). The results show that these differences
affect the behaviour of the PNS convection only little. The flattening
of the
grid). The results show that these differences
affect the behaviour of the PNS convection only little. The flattening
of the
![]() profile appears to be slightly more effective at higher
resolution, see Fig. 10, but the difference is too
small to be distinguishable in other observables. Thus, a resolution
of 2.7
profile appears to be slightly more effective at higher
resolution, see Fig. 10, but the difference is too
small to be distinguishable in other observables. Thus, a resolution
of 2.7
![]() seems sufficient to simulate PNS convection, mainly
because the convective cells have a size of 20
seems sufficient to simulate PNS convection, mainly
because the convective cells have a size of 20
![]() and
are therefore much larger than the size of the angular grid
zones. Similarly, the convective cells are sufficiently small to fit
several times into the angular wedge in each of our simulations.
Boundary conditions are therefore found to have no visible influence,
and our simulation with a full 180
and
are therefore much larger than the size of the angular grid
zones. Similarly, the convective cells are sufficiently small to fit
several times into the angular wedge in each of our simulations.
Boundary conditions are therefore found to have no visible influence,
and our simulation with a full 180
![]() grid revealed no important
differences of PNS convection and of its consequences compared to the
models with a 90
grid revealed no important
differences of PNS convection and of its consequences compared to the
models with a 90
![]() angular wedge.
angular wedge.
The PNS convection also evolves in a similar way in our simulations with
different progenitors. The relative differences compared to the 1D models are quite similar for
all progenitors. Moderate differences,
e.g. in the total energy loss,
![]() ,
between Models s11_32, s15_32, and s20_32, see
Fig. 14, appear small considering the large differences
in the mass accretion rates and post-bounce evolution of these stars.
The evolution of the energy loss is clearly different and lower
only in the rotating Model s15_64_r, where a significant amount of
energy is stored in rotation instead of being radiated by neutrinos.
Also different seed perturbations have little effect on the
evolution of convection in the PNS. Large seeds as, e.g., in Model
s15_64_p, lead to PNS convection which starts typically
10-20 ms earlier. This short time difference of PNS convection,
however, has hardly any influence on the supernova evolution.
,
between Models s11_32, s15_32, and s20_32, see
Fig. 14, appear small considering the large differences
in the mass accretion rates and post-bounce evolution of these stars.
The evolution of the energy loss is clearly different and lower
only in the rotating Model s15_64_r, where a significant amount of
energy is stored in rotation instead of being radiated by neutrinos.
Also different seed perturbations have little effect on the
evolution of convection in the PNS. Large seeds as, e.g., in Model
s15_64_p, lead to PNS convection which starts typically
10-20 ms earlier. This short time difference of PNS convection,
however, has hardly any influence on the supernova evolution.
The structural differences between 1D and 2D models, which are induced
by PNS convection, also influence the layer between the
neutrinospheres and the shock. We can discuss these influences on the
basis of Models s15_32 and s20_32, in which HB convection remains
rather weak so that the differences from 1D result mainly from effects
associated with PNS convection.
In order to understand how much PNS convection
contributes to the differences between 1D and 2D models we have also
performed a 1D simulation, Model s15_mix, for the progenitor s15s7b2,
in which PNS convection was treated with the simple mixing scheme
described in Appendix D. In Fig. 10 we
see that this approximative treatment reproduces the transport of energy
and lepton number by PNS convection rather well. Therefore Model s15_mix
can be understood as a simulation with PNS convection but
without HB convection. Comparing Models s15s7b2, s15_32, and s15_mix,
we conclude that model properties which basically are independent of
the evolution of the gain layer, such as neutrinosphere radii and
neutrino luminosities, are sensitive to PNS convection but not to HB convection (Figs. 11, 12). The
differences between the 1D and 2D models in the gain region, which are
visible in the mass of the gain layer,
![]() ,
the advection
timescale,
,
the advection
timescale,
![]() ,
and the shock radius,
,
and the shock radius,
![]() (Figs. 17, 15), are
initially mainly caused by the HB convection, despite the fact that it
is weak. However, the changes due to PNS convection become gradually
more and more important, and make the dominant influence at the end of
the simulations. In the following we will only discuss the effects
which result from PNS convection. Model s15_mix will therefore also
be considered as a "2D model''.
(Figs. 17, 15), are
initially mainly caused by the HB convection, despite the fact that it
is weak. However, the changes due to PNS convection become gradually
more and more important, and make the dominant influence at the end of
the simulations. In the following we will only discuss the effects
which result from PNS convection. Model s15_mix will therefore also
be considered as a "2D model''.
Note that in
two-dimensional models with downflows and buoyant rising bubbles
in the convective, neutrino-heated layer, Eq. (1)
is not applicable as definition of the advection timescale, and we
therefore use the following definition of an "effective advection
timescale'':
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f250.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg196.gif) |
Figure 15: Maximum and minimum shock radii as functions of time for the 2D models of Table 1, compared to the shock radii of the corresponding 1D models (dotted lines). |
| Open with DEXTER | |
As explained above, PNS convection leads to larger radii of the
neutrinospheres. The mass enclosed by the neutrinospheres, however, is
smaller because of a less compact PNS. The structure of the PNS is
changed such that this also applies for the gain radius and its
enclosed mass, as can be seen for Models s15s7b2, s15_mix, and
s15_32 at late times in Fig. 16. However, the mass
which is enclosed by the standing shock is identical in 1D and 2D models
because it depends on the total mass accreted by the shock and
therefore on the infall region and progenitor structure, which do not
differ between the 1D and 2D models (the shock radius has almost no
influence on the enclosed mass because of the relatively low densities
behind the shock). For these reasons the mass in the gain layer must be
expected to be larger in 2D. The top panel of Fig. 17
confirms this conclusion. We find that the mass in the gain layer,
![]() ,
can be more than a factor of two larger than in 1D. Inevitably, with larger gain radius and larger mass in the gain
layer, the shock radius is also larger than in 1D, see
Fig. 15.
,
can be more than a factor of two larger than in 1D. Inevitably, with larger gain radius and larger mass in the gain
layer, the shock radius is also larger than in 1D, see
Fig. 15.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f260.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg197.gif) |
Figure 16:
Minimum and maximum gain radii as functions of
post-bounce time for our
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f270.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg198.gif) |
Figure 17:
First ( top) panel: mass in the gain layer. Second panel:
advection timescale as defined by Eq. (8). Third
panel: total heating rate in the gain layer. Fourth panel: ratio of
advection timescale to heating timescale. All lines are smoothed
over time intervals of 5 ms. Note that the evaluation of
|
| Open with DEXTER | |
Since the density at a given radius between the neutrinospheres and
the shock is higher in a model with PNS convection (this is a
structural consequence of the larger
![]() -sphere radius, which is
located at
-sphere radius, which is
located at
![]() ), and the mass accretion rate
), and the mass accretion rate
![]() is approximately constant for different radii above the
gain radius (a feature of nearly stationary conditions), and
is approximately constant for different radii above the
gain radius (a feature of nearly stationary conditions), and ![]() is
equal in 1D and 2D (a consequence of the conservation of the mass flow
through the shock), the postshock velocities are (on average) smaller
in 2D. This implies a larger effective advection timescale, see
Fig. 17, second panel. The values of
is
equal in 1D and 2D (a consequence of the conservation of the mass flow
through the shock), the postshock velocities are (on average) smaller
in 2D. This implies a larger effective advection timescale, see
Fig. 17, second panel. The values of
![]() turned out to be larger by up to a factor of
three in the 2D simulations.
turned out to be larger by up to a factor of
three in the 2D simulations.
Astonishingly, we find that the total heating rate of the gain layer,
![]() ,
is almost identical in 1D and 2D
(Fig. 17, third panel). Model s15_mix, however,
reveals that this is a coincidence. A comparison of this model
with Model s15s7b2 shows that PNS convection actually reduces
,
is almost identical in 1D and 2D
(Fig. 17, third panel). Model s15_mix, however,
reveals that this is a coincidence. A comparison of this model
with Model s15s7b2 shows that PNS convection actually reduces
![]() slightly. We will not try to comprehend this
behaviour analytically here, we only mention that the lower
slightly. We will not try to comprehend this
behaviour analytically here, we only mention that the lower
![]() and
and
![]() luminosities and the lower neutrino energies (which the
absorption rates depend on) lead to weaker heating. Also the fact that
the gain radius is larger may contribute to this decrease. We believe
that the larger mass in the gain layer is of minor importance for
luminosities and the lower neutrino energies (which the
absorption rates depend on) lead to weaker heating. Also the fact that
the gain radius is larger may contribute to this decrease. We believe
that the larger mass in the gain layer is of minor importance for
![]() ,
because this additional mass is located at
larger radii where the heating rate is small.
,
because this additional mass is located at
larger radii where the heating rate is small.
Since
![]() increases as a consequence of PNS convection,
also
increases as a consequence of PNS convection,
also
![]() increases. The ratio
increases. The ratio
![]() ,
however,
changes much less (Fig. 17, fourth panel). This can
be understood by the fact that both
,
however,
changes much less (Fig. 17, fourth panel). This can
be understood by the fact that both
![]() and
and
![]() increase due to PNS convection, as explained
above. These changes partly compensate each other in the evaluation of
the timescale ratio.
increase due to PNS convection, as explained
above. These changes partly compensate each other in the evaluation of
the timescale ratio.
In summary, PNS convection has two important consequences: First, the
emitted neutrinos have lower mean energies than in 1D models (up to 10%
lower after 200 ms of PNS convection). The neutrino luminosities
initially decrease due to the onset of PNS convection (
![]() by
about 10% and
by
about 10% and
![]() by about 5%) and increase at later times
(
by about 5%) and increase at later times
(![]() ms post-bounce), to reach several percent higher values
for
ms post-bounce), to reach several percent higher values
for
![]() and even
and even ![]() 20% higher values for
20% higher values for ![]() after 200 ms
of PNS convection. Second, PNS convection affects the evolution of the
gain layer and shock due to a less compact PNS and thus larger
neutrinospheric radii with slightly lower temperatures and
significantly higher luminosities near the neutrinospheres. This leads
to a different structure between neutrinospheres and shock even
without HB convection.
after 200 ms
of PNS convection. Second, PNS convection affects the evolution of the
gain layer and shock due to a less compact PNS and thus larger
neutrinospheric radii with slightly lower temperatures and
significantly higher luminosities near the neutrinospheres. This leads
to a different structure between neutrinospheres and shock even
without HB convection.
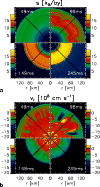 |
Figure 18:
Postshock convection in Model s15_32. Panel a) shows snapshots of
the entropy (in |
| Open with DEXTER | |
We now turn to the discussion of Ledoux-type convection in the gain
layer behind the shock, the so-called "hot bubble'' (HB)
convection. Convective instability starts to develop in this layer in Models s15_32 and s20_32 at about 30 ms after bounce
(Fig. 8), and convective anisotropies
become visible, e.g. in the velocity and
entropy distributions, shortly afterwards
(see Fig. 18). The radial
structure of the star, the shock radius (Fig. 15), and
thus the evolution of the models after bounce are, however, hardly
affected. In this sense the convective activity in the hot-bubble
region is "weak''. The "growth number''
![]() (Eq. (4), Fig. 3) for the
growth of perturbations in the advection flow between shock and gain
radius is correspondingly low. Obviously, neutrino heating is not
powerful enough to drive strong buoyancy against the inward motion of
the advected fluid. The small shock radius is associated with high
negative postshock velocities, thus damping the growth of convection
(for a general discussion, see Foglizzo et al. 2005).
Only during the transient shock expansion, which sets in when the
entropy jump at the Si-SiO interface reaches the shock, does the
advection timescale become sufficiently long to give rise to a phase
of slightly stronger overturn motions.
(Eq. (4), Fig. 3) for the
growth of perturbations in the advection flow between shock and gain
radius is correspondingly low. Obviously, neutrino heating is not
powerful enough to drive strong buoyancy against the inward motion of
the advected fluid. The small shock radius is associated with high
negative postshock velocities, thus damping the growth of convection
(for a general discussion, see Foglizzo et al. 2005).
Only during the transient shock expansion, which sets in when the
entropy jump at the Si-SiO interface reaches the shock, does the
advection timescale become sufficiently long to give rise to a phase
of slightly stronger overturn motions.
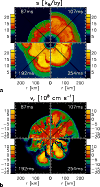 |
Figure 19:
Postshock convection in Model s112_64. Panel a) shows snapshots of
the entropy (in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f300.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg207.gif) |
Figure 20: Mass in the gain layer with the local specific binding energy as defined in Eq. (3) (but normalized per nucleon instead of per unit of mass) above certain values. The results are shown for Models s112_32 and s112_64 for times later than 100 ms after core bounce. |
| Open with DEXTER | |
More powerful HB convection occurs in Model s112_64. As we can see from Fig. 3, the perturbation growth factor increases to values of more than five in simulations with the s112 progenitor when the Si-SiO interface passes the shock 90 ms after bounce. The subsequent expansion of the shock is convectively supported and much stronger than in the 1D model (see Fig. 15). Although there is initially no obvious morphological difference in the convective pattern before and right after the shock expansion (compare Fig. 19, upper left panels with upper right panels), the conditions in case of a larger shock radius become more favorable for a significant strengthening of the neutrino-driven convection, in contrast to the situation in the more massive progenitors, where the composition interface has a much smaller impact. The long advection timescale of 30-40 ms (Fig. 17, 2nd panel) leads to a ratio of advection to heating timescale close to unity (Fig. 17, fourth panel). The mass in the gain layer with specific energy above certain values increases (Fig. 20), the pressure increases, and the shock is pushed to larger radii. The shock is highly deformed and the average shock position therefore fluctuates strongly due to the vigorous convective activity.
We find that in particular large-scale modes of the flow pattern gain strength when the gain layer becomes radially more extended. Besides Ledoux-instability of the neutrino-heated layer, the growth of these modes can be supported by the vortical-acoustic cycle in accretion flows (cf. Foglizzo 2001,2002; and Foglizzo et al. 2005), which has recently been discovered at work during the accretion phase of the stalled supernova shock (Blondin et al. 2003; Ohnishi et al. 2006; Scheck et al. 2004; Blondin & Mezzacappa 2006; Scheck et al., in preparation). The typical wavelength of the most unstable convective modes turns out to be linked to the radial width of the convective shell (for details, see Foglizzo et al. 2005). In Model s112_64 the number of rising high-entropy plumes decreases from five at 50 ms to only two at 107 ms and even only one at 115 ms after bounce (the equatorial bubble in Fig. 19 at 107 ms merges with the other bubble shortly afterwards). Such big structures persist for about 20 ms before they collapse and new rising bubbles form. The pattern is very nonstationary. Also at 140 ms and 170 ms large single bubbles appear, which dissolve again after roughly 20 ms. After the third generation of large bubbles has disappeared, the outer radius of the convective layer shrinks because of shock contraction, and smaller convective cells form again.
The sequence of generations of big, floating bubbles produces an oscillatory behavior of the shock radius (Fig. 15) as a consequence of a kind of feedback cycle between neutrino heating, bubble expansion, shock expansion and overshooting, reduced heating, shock contraction, bubble compression and collapse, increased accretion and heating, new bubble growth, and again shock expansion. This is similar to the oscillatory phases of shock expansion and recession, which we observed for one of the 1D models discussed in Buras et al. (2006, Sect. 3.1.4). In the present 2D situation, however, there is not the same coupling between shock behavior and neutrino luminosities found in that 1D model, where the accretion flow and thus the neutrino luminosities and neutrino heating were quenched during phases of rapid shock expansion. In the multi-dimensional case, downflows of accreted matter around a rising plume can still feed the cooling layer near the neutrinosphere and keep the neutrino luminosities at a high level (see Fig. 12). Here the expansion of the dominant rising plume lowers the heating rate of the bubble material, because its gas moves quickly away from the region of strongest neutrino energy deposition. This means that the expanding plume cuts off its own energy supply. The expansion is, however, still too weak to push the shock outward against the ram pressure of the infalling gas of the progenitor star. After transiently overshooting a possible equilibrium position, the shock therefore turns around, causing the compression of the high-entropy bubble and thus the onset of rapid cooling of the hot bubble gas by neutrino emission. The bubble collapses, and cool gas is channelled from the shock to the gain radius, increasing again the mass in the region of strongest heating. The energy input produces a new rising plume, which drives the shock outward again. The crucial question is whether the energy in the gain layer and the amount of matter with high specific energy increases or decreases during such a feedback cycle. In the first case an explosion may be produced as it happened in the 1D model of Buras et al. (2006) (where it was favored by a manipulation of the neutrino transport). In the present case, however, the feedback cycle ends after three periods (these three periods are visible in Fig. 15 as well as in Fig. 20). The decisive quantity is the ratio of advection to heating timescale, the time-average of which should be larger than unity to obtain net energy gain in the heating layer. For Model s112_64 this is not the case (Fig. 17, bottom panel). Although Model s112_64 gets much closer to success than any of the other simulations because of its strong convection and the large timescale ratio of almost unity, the simulation finally still fails to produce an explosion.
Turning now to resolution studies, we can compare Model s112_64 with Model s112_32. The latter has only half the lateral resolution but is otherwise identical with respect to input physics and radial grid. Clearly, the shock does not expand as far as in the high-resolution model (Fig. 15) and convection does not become as vigorous. Although the tendency of one convective cell to form with one rising plume and one downflow can also be observed in the less resolved model, the convective activity appears weaker and less neutrino-heated matter is involved in the overturn motions (Fig. 20). One reason for this is the fact that downflows become too narrow to be well resolved in the low-resolution model. Their lateral width and stability are therefore numerically overestimated, thus channelling more mass into the cooling layer below the gain radius. Numerical viscosity has a visible influence on the calculation.
Although the resolution in Model s112_64 is probably still not sufficient, the crucial quantity, the timescale ratio, increases only insignificantly when the lateral resolution is improved from 2.7 degrees to 1.35 degrees. We therefore have doubts that a further increase of the resolution can bring the timescale ratio above unity and thus establish favorable conditions for an explosion. Anyway, the resolution in Model s112_64 appears to be the minimal resolution needed for reasonably converged simulations. An angular cell width of one degree would be preferable according to systematic resolution tests (L. Scheck, private communication).
![\begin{figure}
\par\begin{tabular}{lr}
\put(0.9,0.3){{\Large\bf a}}
\includegr...
...f}}
\includegraphics[width=8.2cm]{4654f31f.eps} %
\end{tabular}\par\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg209.gif) |
Figure 21:
Postshock convection in Model s112_128_f. Panels a)-c) show
snapshots of the entropy for six post-bounce times. Panels d)-f)
display the radial velocity at the same times with maximum values of
up to 47 000 km s-1 (bright yellow). In Panel d) also the
convective activity below the neutrinosphere (at radii
|
| Open with DEXTER | |
The size of the seed perturbations for starting convection turns
out not to have an important influence on the HB convection. Comparing
Models s15_32 and s15_64_p we find that a larger seed (as in the
latter model) leads to HB convection which reaches the nonlinear regime
about 10 ms earlier. The subsequent evolution, however,
is very similar, and the
faster onset of convective activity does not have any noticeable
long-time effects. The reason may be the fact that the other relevant
timescales, in particular
![]() and
and
![]() ,
are typically longer than the
perturbation-dependent differences of the growth of HB convection.
,
are typically longer than the
perturbation-dependent differences of the growth of HB convection.
We now discuss Model s112_128_f. The model is different from Model s112_64 in some important technical aspects. The full star was
simulated with a lateral grid of 180
![]() instead of the
instead of the
![]()
![]() wedge around the equatorial plane, which we used
for Model s112_64. Along the polar axis of the spherical grid
the gas flow is reflected, in contrast to our choice of
periodic conditions at the lateral boundaries of the 90
wedge around the equatorial plane, which we used
for Model s112_64. Along the polar axis of the spherical grid
the gas flow is reflected, in contrast to our choice of
periodic conditions at the lateral boundaries of the 90
![]() wedge. Due to the assumed symmetry in case of the 90
wedge. Due to the assumed symmetry in case of the 90
![]() grid, artificial constraints are imposed on the fluid flow.
This has a selective influence on the type of flow
pattern which can develop in the neutrino-heated hot-bubble layer.
Global asymmetries with a dominant contribution of low modes
- i.e., flow with l=1 (dipolar) or l=2 (quadrupolar)
character in terms of orders of an expansion in Legendre polynomials
for the cosine of the polar angle - can, for example, only
be seen when the star as a whole is simulated. The possibility
of long-wavelength modes in the postshock convective zone
of the 11.2
grid, artificial constraints are imposed on the fluid flow.
This has a selective influence on the type of flow
pattern which can develop in the neutrino-heated hot-bubble layer.
Global asymmetries with a dominant contribution of low modes
- i.e., flow with l=1 (dipolar) or l=2 (quadrupolar)
character in terms of orders of an expansion in Legendre polynomials
for the cosine of the polar angle - can, for example, only
be seen when the star as a whole is simulated. The possibility
of long-wavelength modes in the postshock convective zone
of the 11.2![]() simulation is in fact suggested by the
linear perturbation analysis of Foglizzo et al. (2005), because
simulation is in fact suggested by the
linear perturbation analysis of Foglizzo et al. (2005), because
![]() of Eq. (4) reaches values around 6-7 in our 1D run (Fig. 3). Low-mode convection
and global asymmetries of the flow morphology are indeed found
to grow and to cause significant quantitative differences in the
evolution of Model s112_128_f compared to Model s112_64. These
differences are large enough to change the outcome of the simulation
for the 11.2
of Eq. (4) reaches values around 6-7 in our 1D run (Fig. 3). Low-mode convection
and global asymmetries of the flow morphology are indeed found
to grow and to cause significant quantitative differences in the
evolution of Model s112_128_f compared to Model s112_64. These
differences are large enough to change the outcome of the simulation
for the 11.2![]() progenitor even qualitatively.
progenitor even qualitatively.
Noticeable differences between both models occur after about 60 ms post-bounce evolution (see Fig. 21). Although the overall morphology of the flow pattern in the convective postshock layer looks still similar in both simulations, bubbles at the poles of Model s112_128_f extend to larger radii. This is probably a consequence of the numerical setup of the simulation, which assumes axial symmetry and a polar grid with an axis that is impenetrable for the fluid flow. Flow which converges towards the axis is directed either inward or outward. Therefore its motion and behavior are constrained by the existence of the polar grid axis. Moreover, polar features have smaller volumes compared to structures near the equator, which are treated as tori around the symmetry axis. This geometrical difference of polar and equatorial structures is known to lead to differences in the growth rate of perturbations. Laser experiments (Kane et al. 2000) as well as 3D simulations (Scheck 2005) suggest that the smaller axial bubbles can grow faster than equatorial tori and behave more like the mushrooms of Rayleigh-Taylor instabilities in the truely 3D case.
In the further evolution of Model s112_128_f the shock and convective
layer develop a large deformation with dominant dipole and quadrupole
modes, which become more and more prominent. Huge bubbles
inflate alternatingly in both hemispheres, while downflows are present
near the equatorial plane. These downflows are very nonstationary
and flutter back and forth between the hemispheres.
Eventually, 180 ms after bounce, the gain layer is completely dominated
by the two polar bubbles and one or sometimes two downflows
around the equator, separated by a small transient bubble in
between. The shock in this model reaches a radius of about 600 km
at the end of our simulation (Figs. 15 and 22) and is expanding then with a speed
that is typical of exploding models (![]() 10 000 km s-1).
Unfortunately we had to terminate the simulation at 225 ms after bounce
before it was possible to deduce the final parameters of the beginning
explosion. The simulation had to be stopped because of a lack of
computer time and the small timesteps enforced by large and rapid
fluctuations of physical variables in the region where the equatorial
downflow penetrates deep into the neutrinospheric layer.
10 000 km s-1).
Unfortunately we had to terminate the simulation at 225 ms after bounce
before it was possible to deduce the final parameters of the beginning
explosion. The simulation had to be stopped because of a lack of
computer time and the small timesteps enforced by large and rapid
fluctuations of physical variables in the region where the equatorial
downflow penetrates deep into the neutrinospheric layer.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f320.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg211.gif) |
Figure 22: Shock radii at the poles and at the equator versus post-bounce time for Model s112_128_f. |
| Open with DEXTER | |
The polar plumes can be weakened transiently because of the ram pressure of the infalling material ahead of the shock or because of a descreasing supply of neutrino-heated matter when the downflows feed the high-entropy lobe in the opposite hemisphere. But the polar bubbles never collapse and contraction phases are reversed by new, powerful waves of high-entropy, high-velocity matter expanding away from the equatorial plane. The snapshot at 225 ms in Fig. 21 shows such a phase for the hemisphere on the left side (the polar grid axis is oriented horizontally): above 400 km the matter is still expanding, but below it has started retreating due to the ram pressure exerted by the matter falling through the shock. However, from below 300 km a new plume with very high velocities is already reviving the expansion of the gas between 300 km and 400 km. The whole situation is very dynamical.
The dipolar expansion is therefore driven and powered by the
flow of neutrino-heated gas that is continuously replenished near
the gain radius by the equatorial downflow of accreted matter. The
consequences for the dynamical and energetic evolution of Model
s112_128_f can be easily inferred from inspecting global quantities.
In Fig. 17, bottom panel, we see that
the timescale ratio
![]() reaches values above unity in this model. A crucial difference
of Model s112_128_f compared to its 90
reaches values above unity in this model. A crucial difference
of Model s112_128_f compared to its 90
![]() counterparts is the
fact that the advection timescale does not decline again after
its maximum as in the other models but remains essentially constant
for
counterparts is the
fact that the advection timescale does not decline again after
its maximum as in the other models but remains essentially constant
for ![]() ms post bounce. After a period of the order
of
ms post bounce. After a period of the order
of ![]()
![]() the timescale ratio starts rising
monotonically to climb to nearly 1.4 until 180 ms, associated
with an expansion of the average shock radius (Fig. 22).
This means that the dipolar instability has a stronger influence
than Ledoux convection in the other models and leads to an enhancement
of the efficiency of neutrino energy deposition. The total energy transfer
by neutrinos becomes sufficiently large (in fact rises
at
the timescale ratio starts rising
monotonically to climb to nearly 1.4 until 180 ms, associated
with an expansion of the average shock radius (Fig. 22).
This means that the dipolar instability has a stronger influence
than Ledoux convection in the other models and leads to an enhancement
of the efficiency of neutrino energy deposition. The total energy transfer
by neutrinos becomes sufficiently large (in fact rises
at ![]() ms after bounce; Fig. 17)
so that some part of the matter in the gain layer becomes
nominally unbound and strong expansion sets in. Figure 24
shows that the mass of the gas with total local specific energy above
some limits increases continuously, and the mass of the matter with
positive energy follows this trend. Therefore we detect a steep growth
of the "explosion energy'' (Fig. 24, upper panel) after 180 ms. This moment coincides with the accelerated expansion and
marks the onset of the explosion. In
Fig. 12 we see that the neutrino luminosities do not
decrease compared to the luminosities of the non-exploding Model s112_64. This suggests that in spite of the launch of the explosion
neutrino heating will go on at a significant level and will deliver
more energy to the ejecta. Therefore Model s112_128_f does not exhibit
the disadvantageous situation of explosions in spherical
symmetry where the start of rapid shock expansion quenches the
accretion of the forming neutron star and thus leads to a significant
reduction of the neutrino luminosity.
ms after bounce; Fig. 17)
so that some part of the matter in the gain layer becomes
nominally unbound and strong expansion sets in. Figure 24
shows that the mass of the gas with total local specific energy above
some limits increases continuously, and the mass of the matter with
positive energy follows this trend. Therefore we detect a steep growth
of the "explosion energy'' (Fig. 24, upper panel) after 180 ms. This moment coincides with the accelerated expansion and
marks the onset of the explosion. In
Fig. 12 we see that the neutrino luminosities do not
decrease compared to the luminosities of the non-exploding Model s112_64. This suggests that in spite of the launch of the explosion
neutrino heating will go on at a significant level and will deliver
more energy to the ejecta. Therefore Model s112_128_f does not exhibit
the disadvantageous situation of explosions in spherical
symmetry where the start of rapid shock expansion quenches the
accretion of the forming neutron star and thus leads to a significant
reduction of the neutrino luminosity.
The development of large-scale anisotropies with l=1,2 modes was
also seen in other 2D simulations
(Blondin et al. 2003; Ohnishi et al. 2006; Scheck et al. 2004; Burrows et al. 2006) and
occurred in some preliminary 3D simulations
(Mezzacappa & Blondin 2003; L. Scheck, private communication), too.
The morphology of our 180
![]() model looks similar to the models
published by Blondin et al. (2003), who studied the hydrodynamics
of nonradial instabilities of accretion shocks without taking into
account the effects of neutrino transport and neutrino heating.
However, we do not find that the growth of
"turbulent energy'' in the expanding layer behind the shock plays a
significant role for the explosion of Model s112_128_f. In contrast
to the simulations by Blondin et al. (2003),
Model s112_128_f shows a saturation of the kinetic energy of
the lateral gas motions between neutron star (or gain radius)
and shock at times later than
model looks similar to the models
published by Blondin et al. (2003), who studied the hydrodynamics
of nonradial instabilities of accretion shocks without taking into
account the effects of neutrino transport and neutrino heating.
However, we do not find that the growth of
"turbulent energy'' in the expanding layer behind the shock plays a
significant role for the explosion of Model s112_128_f. In contrast
to the simulations by Blondin et al. (2003),
Model s112_128_f shows a saturation of the kinetic energy of
the lateral gas motions between neutron star (or gain radius)
and shock at times later than ![]() 140 ms after bounce on
roughly the same level
140 ms after bounce on
roughly the same level![]() as in Model s112_64.
We neither find specifically large values of
as in Model s112_64.
We neither find specifically large values of
![]() in case of the 180
in case of the 180
![]() simulation, nor
do we see a continuous growth or a
distinct increase of that quantity correlated with the onset of
the explosion and the development of positive values for the
explosion energy after 180 ms (Fig. 23).
We therefore conclude that the explosion of Model s112_128_f is
driven by neutrino energy deposition and not by the amplification
of turbulent kinetic energy in the postshock layer.
simulation, nor
do we see a continuous growth or a
distinct increase of that quantity correlated with the onset of
the explosion and the development of positive values for the
explosion energy after 180 ms (Fig. 23).
We therefore conclude that the explosion of Model s112_128_f is
driven by neutrino energy deposition and not by the amplification
of turbulent kinetic energy in the postshock layer.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f330.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg217.gif) |
Figure 23:
Kinetic energy, as a function of post-bounce time, associated with
the lateral velocities of the matter between
gain radius and shock (solid) and between the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f340.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg219.gif) |
Figure 24:
The upper panel displays the "explosion energy'' of Model s112_128_f, defined by the volume integral of the
"local specific binding energy''
|
| Open with DEXTER | |
Therefore, we have to cautiously interpret the results of our present
simulation. The choice of the lateral grid size and of the boundary conditions
has turned out to decide whether the dipolar instability is suppressed
as in case of the 90
![]() wedge with periodic boundary conditions, or whether
it can develop (and possibly is supported or even enforced) as in case of the
180
wedge with periodic boundary conditions, or whether
it can develop (and possibly is supported or even enforced) as in case of the
180
![]() simulation with axial symmetry and reflecting boundary
conditions along the grid axis. While Model 112_64 with the 90
simulation with axial symmetry and reflecting boundary
conditions along the grid axis. While Model 112_64 with the 90
![]() wedge fails marginally, Model s112_128_f yields an explosion
for the considered
wedge fails marginally, Model s112_128_f yields an explosion
for the considered
![]() progenitor star. Because of the relatively
low mass in the gain layer, the explosion might remain rather weak,
but our simulation had to be terminated too early to be finally
conclusive in this point. The quantitative similarity in many aspects but
qualitative difference in the outcome
of the two simulations demonstrates how close Model 112_64 was already
to an explosion. Conversely, it can also mean that small effects which
weaken the growth of the dipolar instability might delay the onset of
the explosion (and thus change quantities such as the initial mass cut and
the explosion energy), or might even lead to a failure
progenitor star. Because of the relatively
low mass in the gain layer, the explosion might remain rather weak,
but our simulation had to be terminated too early to be finally
conclusive in this point. The quantitative similarity in many aspects but
qualitative difference in the outcome
of the two simulations demonstrates how close Model 112_64 was already
to an explosion. Conversely, it can also mean that small effects which
weaken the growth of the dipolar instability might delay the onset of
the explosion (and thus change quantities such as the initial mass cut and
the explosion energy), or might even lead to a failure![]() .
.
![\begin{figure}
\par\begin{tabular}{cc}
\put(0.9,0.3){{\Large\bf a}}
\includegr...
...bf b}}
\includegraphics[width=8.5cm]{4654f35b.eps} %
\end{tabular} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg221.gif) |
Figure 25:
Radial profiles of the specific angular momentum jz,
angular velocity |
| Open with DEXTER | |
The bottomline is that our 11.2![]() simulation lingers at the
borderline between failure and explosion. But the effect which has
triggered the success in case of Model s112_128_f, i.e. the
large-scale non-radial modes of the fluid flow between shock
and gain radius, can be treated only approximately in two-dimensional
simulations. We can not exclude that the success is a result of
an overestimation of this phenomenon and of its consequences.
Three-dimensional (axis-free) simulations with reliable neutrino
transport are needed to convincingly demonstrate
that the neutrino-driven mechanism, supported by low-mode convection
and accretion shock instability, is viable to explain supernova
explosions of massive stars at least for some range of progenitor
masses.
simulation lingers at the
borderline between failure and explosion. But the effect which has
triggered the success in case of Model s112_128_f, i.e. the
large-scale non-radial modes of the fluid flow between shock
and gain radius, can be treated only approximately in two-dimensional
simulations. We can not exclude that the success is a result of
an overestimation of this phenomenon and of its consequences.
Three-dimensional (axis-free) simulations with reliable neutrino
transport are needed to convincingly demonstrate
that the neutrino-driven mechanism, supported by low-mode convection
and accretion shock instability, is viable to explain supernova
explosions of massive stars at least for some range of progenitor
masses.
![\begin{figure}
\par\begin{tabular}{lr}
\put(0.9,0.3){{\Large\bf a}}
\includegr...
... f}}
\includegraphics[width=8.cm]{4654f36f.eps} %
\end{tabular}\par\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg222.gif) |
Figure 26:
Snapshots of Model s15_64_r. The rotation axis is oriented
vertically. Panels a), b) show the distributions of the
specific angular momentum jz, of the angular frequency |
| Open with DEXTER | |
We investigate the effects of rotation on the supernova
evolution with Model s15_64_r, for which we assume that the iron core rotates with a
period of about 12 s prior to collapse. This is rather slow
compared to the conditions considered in many of the
core-collapse simulations performed by other groups
(e.g., Ott et al. 2004; Kotake et al. 2004). The reasons for our choice of
the initial rotation law were explained in detail at the beginning of
Sect. 3 and in Müller et al. (2004).
The angular frequency ![]() of the
Fe-core at the beginning is 0.5 rad s-1 (Fig. 25) and
increases due to angular momentum conservation during collapse to
maximum values around 600-700 rad s-1 in the homologous core
shortly after bounce, see
Figs. 25, 26a. Rotation generates a
centrifugal force
of the
Fe-core at the beginning is 0.5 rad s-1 (Fig. 25) and
increases due to angular momentum conservation during collapse to
maximum values around 600-700 rad s-1 in the homologous core
shortly after bounce, see
Figs. 25, 26a. Rotation generates a
centrifugal force
![]() which at this time is at most
which at this time is at most
![]() of the gravitational force
of the gravitational force
![]() (Figs. 25, 26a). The ratio of
rotational to gravitational energy,
(Figs. 25, 26a). The ratio of
rotational to gravitational energy,
![]() ,
grows from
an initial value of less than 10-3 to roughly 0.4% at bounce
(Fig. 27). Because of the subsequent contraction
of the PNS and
the inflow of material with higher specific angular momentum (jz),
the ratio
,
grows from
an initial value of less than 10-3 to roughly 0.4% at bounce
(Fig. 27). Because of the subsequent contraction
of the PNS and
the inflow of material with higher specific angular momentum (jz),
the ratio
![]() rises up to 25%
near the equator (Fig. 25) and can reach values around
3 in the polar regions at a post-bounce time of 271.1 ms
(Fig. 26b). The angular frequency
increases up to maximum equatorial values around 2000 rad s-1,
and even much larger values close to the polar axis
(Fig. 26b).
rises up to 25%
near the equator (Fig. 25) and can reach values around
3 in the polar regions at a post-bounce time of 271.1 ms
(Fig. 26b). The angular frequency
increases up to maximum equatorial values around 2000 rad s-1,
and even much larger values close to the polar axis
(Fig. 26b).
As a consequence, the forming neutron star develops an increasing degree
of rotational flattening. The oblateness of the neutrinospheres is most
pronounced during the later stages of the simulated post-bounce
evolution (Fig. 26, panels c, d, f and
Fig. 29), whereas the
deeper interior of the PNS shows a much smaller deformation, and the
convective layer at ![]() km remains nearly spherical
(Fig. 26, panels e, f). At the end of our
simulation the polar value of the radius of the
km remains nearly spherical
(Fig. 26, panels e, f). At the end of our
simulation the polar value of the radius of the
![]() -sphere
is about 30 km, which is roughly the same as in non-rotating models,
whereas the
-sphere
is about 30 km, which is roughly the same as in non-rotating models,
whereas the
![]() -sphere is at 40 km near the equatorial plane
(Figs. 11, 26). Also the
rotation-generated differences of the gain radius
in different directions grow
with time, although the contrast visible in Fig. 16
shows the combined effects of rotation and local variations due to
the convective anisotropies in the postshock region
(see Fig. 26). The angular differences of
the gain radius become roughly a factor of two until the end of our
simulation for Model s15_64_r and are thus somewhat larger than
in the other models
with strong convective overturn in the neutrino-heating layer
(in particular Models s112_64 and s112_128_f). The radial structure
of the rotating PNS differs most strongly from that of the
corresponding non-rotating Model s15_32 near the equatorial plane,
where the centrifugal force,
-sphere is at 40 km near the equatorial plane
(Figs. 11, 26). Also the
rotation-generated differences of the gain radius
in different directions grow
with time, although the contrast visible in Fig. 16
shows the combined effects of rotation and local variations due to
the convective anisotropies in the postshock region
(see Fig. 26). The angular differences of
the gain radius become roughly a factor of two until the end of our
simulation for Model s15_64_r and are thus somewhat larger than
in the other models
with strong convective overturn in the neutrino-heating layer
(in particular Models s112_64 and s112_128_f). The radial structure
of the rotating PNS differs most strongly from that of the
corresponding non-rotating Model s15_32 near the equatorial plane,
where the centrifugal force,
![]() ,
points in the
opposite direction of the gravitational force,
,
points in the
opposite direction of the gravitational force,
![]() .
Differences in the radial structure between the rotating and non-rotating
PNSs are less significant at the poles.
.
Differences in the radial structure between the rotating and non-rotating
PNSs are less significant at the poles.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f370.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg228.gif) |
Figure 27:
Ratio of rotational energy to the gravitational energy,
|
| Open with DEXTER | |
Because of the rotational flattening the PNS as a whole is less compact
than in the non-rotating case, i.e., the volume enclosed by the
neutrinospheres is larger.
The implications of a bigger average neutrinospheric
radius for the global properties of the neutrino emission were
discussed in detail in Sect. 3.1. Due to the lower
temperatures at the more extended neutrinosphere, the mean energies
of the radiated neutrinos are reduced compared to the corresponding
1D model, associated with a decrease of the neutrino luminosities.
In non-rotating models, this reduction holds only for the
first ![]() 150 ms after bounce and is compensated later.
In fact it is over-compensated by the convective energy
transport to the neutrinosphere, which leads to higher luminosities
(in particular for muon and tau neutrinos) in 2D simulations at
150 ms after bounce and is compensated later.
In fact it is over-compensated by the convective energy
transport to the neutrinosphere, which leads to higher luminosities
(in particular for muon and tau neutrinos) in 2D simulations at
![]() ms after bounce (in spite of continuously lower mean
neutrino energies; Figs. 12 and 13).
In the rotating Model s15_64_r this "cooling effect'' of the more
extended neutrinosphere is significantly stronger than in the
corresponding non-rotating Model s15_32, causing even lower
energies of the radiated neutrinos (Fig. 13). In fact,
the neutrinospheric temperatures are reduced so much by rotational
expansion that this effect cannot be overridden by the convective
transport of energy to the neutrinosphere, in particular also because
PNS convection tends to be slightly weaker in Model s15_64_r than
in Model s15_32 (compare Figs. 26 with 5 and see the discussion following later).
The neutrino luminosities in the rotating model stay therefore
clearly below those of its non-rotating counterpart during all of
the simulated evolution (Fig. 12), and the integral of
the radiated energy is smaller than in the 1D case (Fig. 14,
lower panel), signalling that energy is stored in rotation instead of
being converted to neutrino emission. In contrast, the rotating model
does not show a particular behavior with respect to the lepton number
loss (Fig. 14, upper panel), because the electron neutrino
and antineutrino luminosities are both reduced by rotational effects in
very similar ways (Fig. 12). The emission anisotropies
caused by the rotational deformation of the neutrinosphere and by
convective effects will be addressed in Sect. 3.5.
ms after bounce (in spite of continuously lower mean
neutrino energies; Figs. 12 and 13).
In the rotating Model s15_64_r this "cooling effect'' of the more
extended neutrinosphere is significantly stronger than in the
corresponding non-rotating Model s15_32, causing even lower
energies of the radiated neutrinos (Fig. 13). In fact,
the neutrinospheric temperatures are reduced so much by rotational
expansion that this effect cannot be overridden by the convective
transport of energy to the neutrinosphere, in particular also because
PNS convection tends to be slightly weaker in Model s15_64_r than
in Model s15_32 (compare Figs. 26 with 5 and see the discussion following later).
The neutrino luminosities in the rotating model stay therefore
clearly below those of its non-rotating counterpart during all of
the simulated evolution (Fig. 12), and the integral of
the radiated energy is smaller than in the 1D case (Fig. 14,
lower panel), signalling that energy is stored in rotation instead of
being converted to neutrino emission. In contrast, the rotating model
does not show a particular behavior with respect to the lepton number
loss (Fig. 14, upper panel), because the electron neutrino
and antineutrino luminosities are both reduced by rotational effects in
very similar ways (Fig. 12). The emission anisotropies
caused by the rotational deformation of the neutrinosphere and by
convective effects will be addressed in Sect. 3.5.
In contrast to the oblate deformation of the PNS, the shock
reveals a prolate shape during most of the computed evolution,
with a radius typically 50 km larger at the pole than at the
equator (Figs. 15, 26, panels c, d).
The polar bulge of the shock is maintained by a big
convective bubble which exists rather stably between polar angles
of about 10
![]() and about 45
and about 45
![]() .
After an initial, transient
phase in which the convective activity grows and smaller convective
cells merge to larger, volume-filling structures,
this large pole-near bubble comes to exist besides
one or two additional plumes closer to the equator.
Although these bubbles are again strongly time-dependent as in
the other 2D models, and phases of bubble contraction are followed by
bubble reinflation, the morphology is very stable and the bubbles grow
again essentially at the same places. The pattern seems to be
determined and supported by the presence of an angular momentum
gradient in the
neutrino-heated layer (Fig. 26, panel b) and
by the action of centrifugal and coriolis forces on the fluid motion.
.
After an initial, transient
phase in which the convective activity grows and smaller convective
cells merge to larger, volume-filling structures,
this large pole-near bubble comes to exist besides
one or two additional plumes closer to the equator.
Although these bubbles are again strongly time-dependent as in
the other 2D models, and phases of bubble contraction are followed by
bubble reinflation, the morphology is very stable and the bubbles grow
again essentially at the same places. The pattern seems to be
determined and supported by the presence of an angular momentum
gradient in the
neutrino-heated layer (Fig. 26, panel b) and
by the action of centrifugal and coriolis forces on the fluid motion.
Towards the end of our simulation (from about 180 ms
until 280 ms post bounce) quasi-periodic large-amplitude
pole-to-equator oscillations with a cycle time of 15-25 ms
set in (Fig. 15) where phases with a larger
pole-near bubble alternate with time intervals in which the convective
plume near the equator is stronger. The transition between both
extrema is characterized by a merging of the two convective cells
into one big plume at intermediate latitudes. The shape of the shock
changes back and forth between a pronounced prolate deformation and a
more oblate shape. During all these time-dependent variations the
maximum and minimum shock radii stay around 200 km and 150 km,
respectively (Fig. 15). The average shock radius at
![]() ms p.b. is 50-100% larger than in the
non-rotating 2D models and does not decay until the end of our simulation
at nearly 300 ms after bounce. Due to centrifugal effects the
presence of angular momentum in the infalling matter has
a stabilizing influence on the postshock flow and on the shock. Thus
rotation ensures a more extended gain layer and supports strong
convection, in contrast to the non-rotating 15
ms p.b. is 50-100% larger than in the
non-rotating 2D models and does not decay until the end of our simulation
at nearly 300 ms after bounce. Due to centrifugal effects the
presence of angular momentum in the infalling matter has
a stabilizing influence on the postshock flow and on the shock. Thus
rotation ensures a more extended gain layer and supports strong
convection, in contrast to the non-rotating 15![]() Models s15_32 and s15_64_p, where the retraction of the shock after its
maximum expansion strongly damps the convective activity in the gain
layer (Fig. 15; and Buras et al. 2006).
The convective pattern in the postshock region therefore
depends on the amount of angular momentum carried by the
accreted matter. Since the gas falling onto the shock comes from
larger and larger initial radii at later times, the angular momentum
of the accretion flow increases continuously (Fig. 25).
This may explain some of the evolution which we observe for the
morphology and dynamical behavior of the convective post-shock layer.
Models s15_32 and s15_64_p, where the retraction of the shock after its
maximum expansion strongly damps the convective activity in the gain
layer (Fig. 15; and Buras et al. 2006).
The convective pattern in the postshock region therefore
depends on the amount of angular momentum carried by the
accreted matter. Since the gas falling onto the shock comes from
larger and larger initial radii at later times, the angular momentum
of the accretion flow increases continuously (Fig. 25).
This may explain some of the evolution which we observe for the
morphology and dynamical behavior of the convective post-shock layer.
The conditions for convective instability are affected by rotation
in a way which is expressed by the so-called Solberg-Høiland
criteria (see e.g. Tassoul 1978; Keil 1997). For the considered
situation in the supernova core, the first criterion is a
generalization of our Quasi-Ledoux criterion, combined with the
Solberg-term which accounts for the stabilizing effect of a
positive angular momentum gradient. With
the parameter
![]() for neutrino diffusion in the
Quasi-Ledoux criterion (Eq. (7)), the corresponding
mode frequencies are
for neutrino diffusion in the
Quasi-Ledoux criterion (Eq. (7)), the corresponding
mode frequencies are
| |
![$\displaystyle {}- \frac{
(\vec{\nabla} \phi - \vec{a}_{\rm cent})_z}{\rho}
\lef...
...t\vert _{p,s_{\rm tot}}
\frac{{\rm d}{Y_{\rm lep}}~}{{\rm d}z~} \right] \right.$](/articles/aa/full/2006/37/aa4654-05/img237.gif) |
||
![$\displaystyle {} \left. - \frac{{\rm d}j_z^2~}{{\rm d}z~}
\left[ \left.\frac{\p...
..._{p,s_{\rm tot}}
\frac{{\rm d}{Y_{\rm lep}}~}{{\rm d}x~} \right] \right\} > 0~,$](/articles/aa/full/2006/37/aa4654-05/img238.gif) |
(10) |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f380.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg240.gif) |
Figure 28:
|
| Open with DEXTER | |
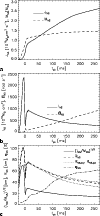 |
Figure 29:
a) Mass
|
| Open with DEXTER | |
As already discussed in earlier publications (Janka & Keil 1998; Janka et al. 2001; Keil 1997) the differential rotation, which is accounted for by the first term in Eq. (9), tends to damp convective activity near the polar axis in the PNS, see Figs. 26e,f. The same effect is found for the hot-bubble layer, see Figs. 26c,d. At larger distances from the polar axis the distribution of the specific angular momentum is flatter and convection is only weakly affected by rotation, i.e. convection develops in regions inside the PNS and between the gain radius and the shock basically similar to the situation in Model s15_32. PNS convection therefore has effects analogous to those discussed in Sect. 3.1. The damping of convection near the poles leads to a slightly slower effective transport of lepton number (and energy), see Fig. 28 for the situation after 200 ms post-bounce evolution, especially at later times when the convection near the axis is more strongly suppressed due to a steeper gradient of jz, see Figs. 26e,f. Another new feature in the rotating model is the transport and redistribution of angular momentum by convection. Figure 25b shows how convection in the PNS produces a flat radial profile of jz near the equator. This happens despite the stabilizing effect of the initially positive derivative of jz because the negative entropy gradient dominates the Solberg-Høiland criterion and drives convective instability.
How does rotation affect the possibility for getting explosions
by the delayed neutrino-heating mechanism? The analysis by Yamasaki & Yamada (2005)
suggests that rotation can appreciably improve the conditions for
shock revival in case the initial rotation frequency is at least
![]() Hz at 1000 km. This corresponds to a rotation period of 10 s and is therefore only slightly faster than the rotation
considered in Model s15_64_r (where the initial spin period is 12 s
in the iron core). Yamasaki & Yamada (2005) found a sizable reduction by 25% of
the "critical neutrino luminosity'' for starting a neutrino-driven
explosion at a mass accretion rate of about 1
Hz at 1000 km. This corresponds to a rotation period of 10 s and is therefore only slightly faster than the rotation
considered in Model s15_64_r (where the initial spin period is 12 s
in the iron core). Yamasaki & Yamada (2005) found a sizable reduction by 25% of
the "critical neutrino luminosity'' for starting a neutrino-driven
explosion at a mass accretion rate of about 1![]() s-1 or lower.
The effects of rotation are, however, diverse and modify the structure
of the collapsing star, the convection in the core, the gas motion
behind the shock, and the radius and neutrino
emission of the forming neutron star. A separate discussion
of selected effects as done by Yamasaki & Yamada (2005) can therefore be
misleading. In our simulations all effects of rotation are fully
coupled and we can assess the question how these effects in combination
determine the conditions for the delayed explosion mechanism. To this
end we again compare the results of our rotating model with the
non-rotating counterparts.
s-1 or lower.
The effects of rotation are, however, diverse and modify the structure
of the collapsing star, the convection in the core, the gas motion
behind the shock, and the radius and neutrino
emission of the forming neutron star. A separate discussion
of selected effects as done by Yamasaki & Yamada (2005) can therefore be
misleading. In our simulations all effects of rotation are fully
coupled and we can assess the question how these effects in combination
determine the conditions for the delayed explosion mechanism. To this
end we again compare the results of our rotating model with the
non-rotating counterparts.
Rotation turns out to be helpful, but to a much lesser extent than
estimated by Yamasaki & Yamada (2005). Certainly, the shock radius is
significantly larger than in the non-rotating models of the 15![]() star (Fig. 15), the effective advection
timescale
star (Fig. 15), the effective advection
timescale
![]() through the gain layer correspondingly
becomes longer by up to a factor of about 4, and the mass in the gain
layer,
through the gain layer correspondingly
becomes longer by up to a factor of about 4, and the mass in the gain
layer,
![]() ,
increases to a value that is two or three times
larger than in the non-rotating models.
These differences are on the one hand an
indirect consequence of the structural changes of the PNS (cf. Sect. 3.1), on the other hand they result directly from the
influence of centrifugal forces on the fluid flow in the gain layer.
In contrast, however, the total heating rate,
,
increases to a value that is two or three times
larger than in the non-rotating models.
These differences are on the one hand an
indirect consequence of the structural changes of the PNS (cf. Sect. 3.1), on the other hand they result directly from the
influence of centrifugal forces on the fluid flow in the gain layer.
In contrast, however, the total heating rate,
![]() ,
and the ratio of advection
to heating timescale increase only slightly (Fig. 17).
The latter remains significantly below unity, because the heating
timescale
,
and the ratio of advection
to heating timescale increase only slightly (Fig. 17).
The latter remains significantly below unity, because the heating
timescale
![]() has increased considerably
due to the lower energies
and luminosities of the neutrinos radiated from the rotating PNS
(Figs. 12, 13). The rotating model therefore
shows no tendency to develop an explosion until we stopped our simulation
at about 280 ms after bounce.
has increased considerably
due to the lower energies
and luminosities of the neutrinos radiated from the rotating PNS
(Figs. 12, 13). The rotating model therefore
shows no tendency to develop an explosion until we stopped our simulation
at about 280 ms after bounce.
If angular momentum conservation holds during the subsequent
evolution, one can use our results at the end of the simulated evolution
to roughly estimate the final angular frequency of the cold neutron star
after its neutrino cooling and contraction phase,
![]() ,
assuming it to be a rigid
rotator. The "NS'' is defined here as the mass at densities above
,
assuming it to be a rigid
rotator. The "NS'' is defined here as the mass at densities above
![]() .
In Fig. 29 we show the time evolution
of several quantities for this such defined "NS'', namely of the
radius
.
In Fig. 29 we show the time evolution
of several quantities for this such defined "NS'', namely of the
radius
![]() ,
defined as the radius of a sphere with the
same volume as the deformed proto-neutron star, and of the average
angular frequency, defined as
,
defined as the radius of a sphere with the
same volume as the deformed proto-neutron star, and of the average
angular frequency, defined as
![]() ,
where
,
where
![]() is the moment of inertia and
is the moment of inertia and
![]() is the
total angular momentum of the "NS''. Taking the conditions at
t=270 ms after bounce and assuming angular momentum convervation - no
processes happen which transport angular momentum out of the NS or add
mass and angular momentum to it -, the angular frequency of the NS
after self-similar contraction (i.e., the shape of the
star does not change and thus its moment of inertia scales with the
square of the average NS radius)
to a final radius
is the
total angular momentum of the "NS''. Taking the conditions at
t=270 ms after bounce and assuming angular momentum convervation - no
processes happen which transport angular momentum out of the NS or add
mass and angular momentum to it -, the angular frequency of the NS
after self-similar contraction (i.e., the shape of the
star does not change and thus its moment of inertia scales with the
square of the average NS radius)
to a final radius
![]() km is
km is
In this section we shall discuss the variations of the neutrino
emission with polar angle, which are a consequence of PNS convection,
convective overturn in the layer between gain radius and shock, and of
rotation. For this purpose we will mostly concentrate on the non-rotating
Model s112_128_f, which develops extremely strong convection and
anisotropy, and on our case with rotation, Model s15_64_r.
The anisotropy of the neutrino emission from rotating collapsing
stellar cores was first evaluated by Janka & Mönchmeyer (1989b,a)
analytically and by means of post-processing Monte Carlo transport
calculations using 2D core-collapse models. They found that the neutrino
emission is higher in the polar direction than in the equatorial plane,
verifying von Zeipel's law of gravity darkening in case of neutrinos from
supernova cores. This result was confirmed
by Kotake et al. (2003), who
also performed a post-processing analysis of 2D core-collapse calculations
in which a trapping scheme for the neutrino treatment was employed.
It must be pointed out, however, that none of these approaches was
self-consistent: the emission anisotropy and the neutrino treatment in
the hydrodynamic simulations were calculated with different approximative
methods, the feedback of neutrino transport on the hydrodynamics was
not taken into account (a trapping scheme only computes local source
terms), and the evaluation was based on simplifying concepts, e.g.,
the assumption that a well-defined average
neutrinosphere exists![]() .
The calculated anisotropies must therefore be interpreted with great
caution and conclusions drawn on their basis may be very misleading,
in particular concerning their implications for the explosion mechanism.
The latter depends on many competing effects and a discussion requires
a coupled and consistent treatment of neutrinos and hydrodynamics.
Walder et al. (2005) recently
performed such simulations of rotational core collapse, in which
2D flux-limited neutrino diffusion was followed self-consistently in
2D hydrodynamic models. These authors pointed out the fact that the
neutrino emission is always more isotropic than the rotationally deformed
or convectively distorted mass distribution because of the non-locality
of the transport, i.e., the neutrino distribution at every point is a
superposition of the irradiation from different contributing directions.
The paper by Walder et al. (2005), however, does not provide
quantitative information in a form which would allow
us to make comparisons with their results. In the following we will
therefore concentrate on the presentation and discussion of our models.
.
The calculated anisotropies must therefore be interpreted with great
caution and conclusions drawn on their basis may be very misleading,
in particular concerning their implications for the explosion mechanism.
The latter depends on many competing effects and a discussion requires
a coupled and consistent treatment of neutrinos and hydrodynamics.
Walder et al. (2005) recently
performed such simulations of rotational core collapse, in which
2D flux-limited neutrino diffusion was followed self-consistently in
2D hydrodynamic models. These authors pointed out the fact that the
neutrino emission is always more isotropic than the rotationally deformed
or convectively distorted mass distribution because of the non-locality
of the transport, i.e., the neutrino distribution at every point is a
superposition of the irradiation from different contributing directions.
The paper by Walder et al. (2005), however, does not provide
quantitative information in a form which would allow
us to make comparisons with their results. In the following we will
therefore concentrate on the presentation and discussion of our models.
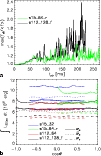 |
Figure 30:
a) Lateral maxima of the
|
| Open with DEXTER | |
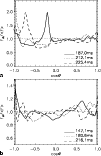 |
Figure 31:
a) Ratio of electron neutrino flux to average flux (for an
observer at rest at 400 km) versus cosine of the polar angle for
Model s112_128_f for different post-bounce times. The times are
picked such that large maxima of the flux ratio occur (see
Fig. 30a).
b) Same as panel a, but at the
|
| Open with DEXTER | |
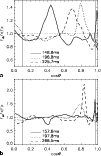 |
Figure 32:
Same as Fig. 31, but for Model s15_64_r.
The pole of the rotating model corresponds to
|
| Open with DEXTER | |
Because the downflows are transient in space and time, the lateral variations disappear in the time-integrated flux at different latitudes, and only minor fluctations remain (Fig. 30b). Local maxima or minima at the lateral edges are a consequence of the reflecting boundary conditions, which cannot be penetrated but redirect the flow in the inward or outward direction.
The flux ratio maxima for Model s15_64_r also exhibit short-time variations with typical fluctuation timescales of about 5 ms, but with lower amplitudes (up to values of 1.5) than those in Model s112_128_f. This is mainly due to the fact that the convective layer in Model s15_64_r has a smaller radial extension, the downflows are less narrow and hit the cooling layer with less violence, producing less extreme local emission than in Model s112_128_f. An exception to this is the polar region of the rotating model, where the accretion flow is able to create a high-luminosity spot even at the neutrinosphere, causing larger latitudinal flux variations there than farther out (Figs. 32a,b).
While the time-integrated flux at large distances reveals a local maximum near the equator in Model s15_64_r (Fig. 30b), which is associated with a persistent equatorial downflow, the time-integrated flux at the neutrinosphere is nearly featureless with only a very shallow global pole-to-equator gradient. The latter is a consequence of the rotational flattening of the PNS, which, however, is too low to have significant effects on the instantaneous (Figs. 32b) or time-integrated (Fig. 30b) neutrinospheric emission.
We point out that a discussion of the lateral variation of the neutrino emission of our models is handicapped by the fact that our approximation of 2D neutrino transport disregards the lateral component of the neutrino flux vector and therefore tends to overestimate the angular asymmetry of neutrinos streaming out from radiating regions (for a more detailed discussion, see Buras et al. 2006). Truely multi-dimensional transport should therefore not only reveal smaller lateral variations of the time-integrated flux as our models do, but will also show less extreme angular variations of the instantaneous emission on short spatial wavelengths.
We have presented results of a series of core-collapse and
post-bounce simulations for different progenitor stars between 11.2![]() and 25
and 25![]() ,
comparing 2D (axially symmetric)
with 1D (spherically symmetric) calculations. Doing so, our main
goals were (i) investigating the differences between convection
in progenitors with different masses; (ii) exploring the
effects of convection below the neutrinosphere ("PNS convection'')
on the proto-neutron star structure, its neutrino emission, and
the neutrino heating-layer behind the shock;
(iii) investigating the role of hydrodynamic instabilities that
affect the stalled accretion shock, i.e. convective overturn in the
neutrino-heated "hot bubble'' layer ("HB convection'') and global
low-mode nonradial instability of the accretion shock (termed SASI
by Blondin et al. 2003; and possibly caused by the action of
an advective-acoustic cycle according to Foglizzo 2001,2002);
(iv) studying the effects of rotation; and (v) testing the influence
of numerical aspects like the grid resolution, size of the angular
wedge, and magnitude of seed perturbations for convection.
Since our 2D neutrino-hydrodynamics code is a direct
descendant of our 1D PROMETHEUS/VERTEX code, it is
particularly well suited for performing such comparisons of 1D
and 2D supernova models.
,
comparing 2D (axially symmetric)
with 1D (spherically symmetric) calculations. Doing so, our main
goals were (i) investigating the differences between convection
in progenitors with different masses; (ii) exploring the
effects of convection below the neutrinosphere ("PNS convection'')
on the proto-neutron star structure, its neutrino emission, and
the neutrino heating-layer behind the shock;
(iii) investigating the role of hydrodynamic instabilities that
affect the stalled accretion shock, i.e. convective overturn in the
neutrino-heated "hot bubble'' layer ("HB convection'') and global
low-mode nonradial instability of the accretion shock (termed SASI
by Blondin et al. 2003; and possibly caused by the action of
an advective-acoustic cycle according to Foglizzo 2001,2002);
(iv) studying the effects of rotation; and (v) testing the influence
of numerical aspects like the grid resolution, size of the angular
wedge, and magnitude of seed perturbations for convection.
Since our 2D neutrino-hydrodynamics code is a direct
descendant of our 1D PROMETHEUS/VERTEX code, it is
particularly well suited for performing such comparisons of 1D
and 2D supernova models.
Convection inside the proto-neutron star starts 30-40 ms
after bounce in all of our 2D models and encompasses a layer
growing in mass until the end of our simulations (which were typically
terminated about 250 ms after bounce). It leads to a more extended
neutron star than in the 1D simulations with lower temperatures at
the neutrinosphere. For this reason the mean energies of the neutrinos
emitted from the neutrinosphere are reduced (up to 10% after 200 ms
of PNS convection). Despite the larger
radiating surface, the lower neutrinospheric temperatures also
cause a slight reduction of neutrino luminosities during the first 150 ms after bounce. This holds in particular for
![]() ,
because the convective transport of lepton
number maintains a higher electron degeneracy in the neutrinospheric
region and accelerates the lepton number loss compared to 1D simulations. Only at
,
because the convective transport of lepton
number maintains a higher electron degeneracy in the neutrinospheric
region and accelerates the lepton number loss compared to 1D simulations. Only at ![]() ms after bounce,
convectively enhanced energy transport in the nascent neutron star
also leads to increased energy loss, and the luminosities of
heavy-lepton neutrinos become significantly
(15%-20%) higher than in the spherical models.
ms after bounce,
convectively enhanced energy transport in the nascent neutron star
also leads to increased energy loss, and the luminosities of
heavy-lepton neutrinos become significantly
(15%-20%) higher than in the spherical models.
PNS convection of the kind found in our simulations leads to
a slightly reduced total
energy deposition in the gain layer mainly because of the lower
average energies of the radiated
![]() and
and
![]() .
Since the effects of convection below
the neutrinosphere are hard to disentangle from those of hydrodynamic
instabilities in the neutrino-heating layer behind the stalled shock,
we developed a simple "mixing algorithm''. It allowed us to
reproduce all major effects of PNS convection in 1D simulations
and thus to separate them from the consequences of multi-dimensional
fluid flow in the postshock layer and to arrive at the above
conclusion.
.
Since the effects of convection below
the neutrinosphere are hard to disentangle from those of hydrodynamic
instabilities in the neutrino-heating layer behind the stalled shock,
we developed a simple "mixing algorithm''. It allowed us to
reproduce all major effects of PNS convection in 1D simulations
and thus to separate them from the consequences of multi-dimensional
fluid flow in the postshock layer and to arrive at the above
conclusion.
Convective overturn in the neutrino-heating layer remained rather
weak in case of the 15![]() and 20
and 20![]() progenitors.
The main reason for that is the rapid contraction of the accretion
shock after its maximum expansion. This causes the gain layer to
be very narrow and the infall velocities of the gas ahead and
behind the shock to be very high. As a consequence, the advection
timescale of the gas through the gain layer is very short
compared to the typical neutrino-heating timescale. Buoyancy
forces therefore hardly achieve bubble rise in the flow of gas
accreted from the shock to the gain radius. As suggested by
Janka & Keil (1998) and Janka et al. (2001) and verified by
Thompson et al. (2005), the ratio of the advection timescale to the
neutrino-heating timescale,
progenitors.
The main reason for that is the rapid contraction of the accretion
shock after its maximum expansion. This causes the gain layer to
be very narrow and the infall velocities of the gas ahead and
behind the shock to be very high. As a consequence, the advection
timescale of the gas through the gain layer is very short
compared to the typical neutrino-heating timescale. Buoyancy
forces therefore hardly achieve bubble rise in the flow of gas
accreted from the shock to the gain radius. As suggested by
Janka & Keil (1998) and Janka et al. (2001) and verified by
Thompson et al. (2005), the ratio of the advection timescale to the
neutrino-heating timescale,
![]() ,
turned out to be a
useful diagnostic parameter to measure the proximity of a model
to a neutrino-driven explosion. A necessary
condition for an explosion is that the timescale ratio rises
above unity for a time interval of at least the neutrino-heating
timescale. In case of the 15
,
turned out to be a
useful diagnostic parameter to measure the proximity of a model
to a neutrino-driven explosion. A necessary
condition for an explosion is that the timescale ratio rises
above unity for a time interval of at least the neutrino-heating
timescale. In case of the 15![]() and 20
and 20![]() models,
HB convection increases the heating rate and the timescale ratio
to values only slightly larger than in the 1D simulations, but
still roughly a factor of two below the critical limit.
We therefore found explosions of these stars neither in
spherical symmetry (in agreement with Liebendörfer et al. 2002;
Thompson et al. 2003; Sumiyoshi et al. 2005) nor in 2D.
models,
HB convection increases the heating rate and the timescale ratio
to values only slightly larger than in the 1D simulations, but
still roughly a factor of two below the critical limit.
We therefore found explosions of these stars neither in
spherical symmetry (in agreement with Liebendörfer et al. 2002;
Thompson et al. 2003; Sumiyoshi et al. 2005) nor in 2D.
Also rotation did not change this negative outcome. We studied
one 15![]() model with pre-collapse rigid iron core rotation
of
model with pre-collapse rigid iron core rotation
of ![]() 12 s period, which leads to a
neutron star with a spin period of about 1 ms, if the angular
momentum of the core after collapse is conserved.
Rotation of this size is probably on
the extreme side of what can be expected for the cores of "normal''
supernovae, which are supposed to give birth to neutron stars
with an initial period of 10 ms or more (see the discussions
in Heger et al. 2005; and Ott et al. 2006). Our simulations
reveal a number of important differences of the rotating model
compared to its non-rotating counterparts. The proto-neutron star
develops an eccentricity of more than 0.6 until we stopped the
simulation at nearly 300 ms after bounce. At this time
the luminosities of the radiated neutrinos are significantly
smaller (10-20%) and their mean energies up to 2 MeV lower
than in the non-rotating 2D model, because the equatorially
more extended neutrinosphere is significantly cooler and energy
is stored in rotation instead of being released by neutrinos.
Despite the clear oblateness of the proto-neutron star, its
rotation-induced emission anisotropy is very small.
Nevertheless, rotation has a favorable influence on the
conditions and parameters which determine neutrino-driven
explosions. Centrifugal forces stabilize the accretion shock at
larger radii, increase the advection timescale of the postshock
gas significantly, and thus allow for a layer of well developed,
strong convective overturn activity behind the shock.
Because more mass stays in the gain
layer for a longer time, the total energy deposition rate behind
the shock is higher at later post-bounce times (
12 s period, which leads to a
neutron star with a spin period of about 1 ms, if the angular
momentum of the core after collapse is conserved.
Rotation of this size is probably on
the extreme side of what can be expected for the cores of "normal''
supernovae, which are supposed to give birth to neutron stars
with an initial period of 10 ms or more (see the discussions
in Heger et al. 2005; and Ott et al. 2006). Our simulations
reveal a number of important differences of the rotating model
compared to its non-rotating counterparts. The proto-neutron star
develops an eccentricity of more than 0.6 until we stopped the
simulation at nearly 300 ms after bounce. At this time
the luminosities of the radiated neutrinos are significantly
smaller (10-20%) and their mean energies up to 2 MeV lower
than in the non-rotating 2D model, because the equatorially
more extended neutrinosphere is significantly cooler and energy
is stored in rotation instead of being released by neutrinos.
Despite the clear oblateness of the proto-neutron star, its
rotation-induced emission anisotropy is very small.
Nevertheless, rotation has a favorable influence on the
conditions and parameters which determine neutrino-driven
explosions. Centrifugal forces stabilize the accretion shock at
larger radii, increase the advection timescale of the postshock
gas significantly, and thus allow for a layer of well developed,
strong convective overturn activity behind the shock.
Because more mass stays in the gain
layer for a longer time, the total energy deposition rate behind
the shock is higher at later post-bounce times (
![]() ms p.b.)
than in the non-rotating models. In spite of these healthy effects,
however, the timescale ratio
ms p.b.)
than in the non-rotating models. In spite of these healthy effects,
however, the timescale ratio
![]() remains still well below unity
(
remains still well below unity
(
![]() ).
).
Even without rotation postshock convection becomes violent in case
of the 11.2
![]() star. The shock in this
model is able to stay longer at large radii than in the more
massive stars. This is due to the fact that the rather low-mass
progenitor has a steeper density decline at the transition to
the Si+O layer, which leads to a rapid
decrease of the mass accretion rate of the shock at about 90 ms
after bounce. This allows the shock to reexpand in adjusting to
the situation of reduced ram pressure. The increased advection
timescale gives convection the possibility to gain strength
and thus to support the shock at a much larger radius than in
the corresponding 1D model. Also the total neutrino heating rate
behind the shock and the efficiency of net neutrino-energy
transfer to the gas in the gain layer is higher by up to a factor
of two. The timescale ratio
star. The shock in this
model is able to stay longer at large radii than in the more
massive stars. This is due to the fact that the rather low-mass
progenitor has a steeper density decline at the transition to
the Si+O layer, which leads to a rapid
decrease of the mass accretion rate of the shock at about 90 ms
after bounce. This allows the shock to reexpand in adjusting to
the situation of reduced ram pressure. The increased advection
timescale gives convection the possibility to gain strength
and thus to support the shock at a much larger radius than in
the corresponding 1D model. Also the total neutrino heating rate
behind the shock and the efficiency of net neutrino-energy
transfer to the gas in the gain layer is higher by up to a factor
of two. The timescale ratio
![]() approaches unity and remains close to - but slightly below - this
threshold until the end of our simulations. The 11.2
approaches unity and remains close to - but slightly below - this
threshold until the end of our simulations. The 11.2
![]() model computed with a 90
model computed with a 90
![]() lateral wedge therefore lingers
at the border to success.
lateral wedge therefore lingers
at the border to success.
Such a situation is extremely sensitive to relatively little
changes. We saw this when we repeated the simulation with a full 180
![]() grid instead of using the wedge around the equator.
While PNS convection turned out not to depend on the wedge size,
convective activity in the neutrino-heating layer can change
significantly when the available degrees of freedom are not
constrained by periodic boundary conditions of a 90
grid instead of using the wedge around the equator.
While PNS convection turned out not to depend on the wedge size,
convective activity in the neutrino-heating layer can change
significantly when the available degrees of freedom are not
constrained by periodic boundary conditions of a 90
![]() equatorial wedge and therefore low-mode deformation of dipolar
(l = 1) and quadrupolar (l = 2) character is allowed for.
Convection becomes sufficiently
strong so that the accretion shock continues to expand.
This ensures that the effective advection timescale
does not decrease after it has reached its maximum.
At
equatorial wedge and therefore low-mode deformation of dipolar
(l = 1) and quadrupolar (l = 2) character is allowed for.
Convection becomes sufficiently
strong so that the accretion shock continues to expand.
This ensures that the effective advection timescale
does not decrease after it has reached its maximum.
At
![]() ms after bounce, the timescale ratio
ms after bounce, the timescale ratio
![]() then becomes larger than
unity, thus further improving the conditions for efficient energy
deposition by neutrinos in the postshock layer. After about
180 ms of post-bounce evolution the total energy in the gain layer becomes positive and continues rising because the mass in
the gain layer and the energy per nucleon grow. The model has
passed the critical threshold and is on its way to explosion.
A closer inspection of the involved energies shows that this
explosion is powered by neutrino heating.
then becomes larger than
unity, thus further improving the conditions for efficient energy
deposition by neutrinos in the postshock layer. After about
180 ms of post-bounce evolution the total energy in the gain layer becomes positive and continues rising because the mass in
the gain layer and the energy per nucleon grow. The model has
passed the critical threshold and is on its way to explosion.
A closer inspection of the involved energies shows that this
explosion is powered by neutrino heating.
This qualitative difference of the outcome of 2D simulations with 90
![]() and 180
and 180
![]() grids is another confirmation of the
proximity of our
2D simulations, and in particular of the 11.2
grids is another confirmation of the
proximity of our
2D simulations, and in particular of the 11.2
![]() case,
to a success of the convectively supported neutrino-driven mechanism.
Together with the recent models for stars in the
case,
to a success of the convectively supported neutrino-driven mechanism.
Together with the recent models for stars in the
![]() range with O-Ne-Mg cores, which explode even
in spherical symmetry (Kitaura et al. 2006), our current results seem to
indicate that the neutrino-heating mechanism is viable at least
for stars near the low-mass end of supernova progenitors.
range with O-Ne-Mg cores, which explode even
in spherical symmetry (Kitaura et al. 2006), our current results seem to
indicate that the neutrino-heating mechanism is viable at least
for stars near the low-mass end of supernova progenitors.
The sensitivity to numerical variations, however, also stresses the need to remove some of the shortcomings and limitations of axially symmetric simulations. One must suspect that in 3D simulations morphological differences of the structures (plumes instead of azimuthal tori), different growth rates of instabilities, or additional degrees of freedom (e.g. triaxial asymmetries and vortex motion caused by Coriolis forces) might lead to sizable quantitative differences which could be crucial when collapsing stellar cores are close to the threshold for explosion. Also the existence of the polar axis of a spherical or cylindrical coordinate grid is a potential source of numerical uncertainties, because it is a coordinate singularity which is impenetrable for approaching fluid flow and thus defines a preferred grid direction.
Our results therefore suggest the need to strive for 3D simulations, preferentially without the disadvantages connected with the polar grid axis. The importance of low-mode convection or low-mode hydrodynamical instabilities as suggested by our results implies that such simulations will have to be done for the full star and cannot be contrained to a limited wedge.
Acknowledgements
We are grateful to Almudena Arcones, Francisco Kitaura, Andreas Marek, and Leonhard Scheck for many helpful discussions and to an anonymous referee for careful reading and a long list of useful comments. Support by the Sonderforschungsbereich 375 on "Astro-Particle Physics'' of the Deutsche Forschungsgemeinschaft is acknowledged. The computations were performed on the NEC SX-5/3C and the IBM p690 "Regatta'' system of the Rechenzentrum Garching, and on the Cray T90 and IBM p690 "Jump'' of the John von Neumann Institute for Computing (NIC) in Jülich.
Table A.1:
List of progenitors used in the simulations.
![]() and
and
![]() are the enclosed masses at composition
interfaces defined by entropy jumps. With (e) we denote that a shell
interface is connected with a gradual enrichment of the lighter nucleus,
i.e. these cases are Fe-FeSi and Si-SiO interfaces where the mass
fractions of Si or O grows gradually outwards. The underlined numbers
indicate an entropy increase of more than
are the enclosed masses at composition
interfaces defined by entropy jumps. With (e) we denote that a shell
interface is connected with a gradual enrichment of the lighter nucleus,
i.e. these cases are Fe-FeSi and Si-SiO interfaces where the mass
fractions of Si or O grows gradually outwards. The underlined numbers
indicate an entropy increase of more than
![]() per nucleon
in case of an Fe-Si interface and an entropy increase of more than
per nucleon
in case of an Fe-Si interface and an entropy increase of more than
![]() /by in case of a Si-O interface.
/by in case of a Si-O interface.
![\begin{figure}
\includegraphics[width=12cm,clip]{4654f010.eps} \end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg269.gif) |
Figure A.1:
The progenitor data for temperature T, electron
fraction
|
The properties of the nine progenitor models used in this work
are summarized in Fig. A.1 and Table A.1.
In Fig. A.1 the initial
pre-collapse data as given by the stellar evolution modelers are
displayed, in Figs. A.2 and A.3 we compare the
cores at a central density of
![]() ,
which was reached by evolving the models with our 1D Boltzmann
transport code VERTEX. Up to this point the infall velocities are
still subsonic and neutrinos stream off almost unhindered. Compared to
the original progenitor data in Fig. A.1 the electron
number
,
which was reached by evolving the models with our 1D Boltzmann
transport code VERTEX. Up to this point the infall velocities are
still subsonic and neutrinos stream off almost unhindered. Compared to
the original progenitor data in Fig. A.1 the electron
number
![]() has changed significantly and strongest for those models
which started out with the lowest initial densities at the center. The
evolution proceeded nearly adiabatically, the entropy changes are
therefore small.
has changed significantly and strongest for those models
which started out with the lowest initial densities at the center. The
evolution proceeded nearly adiabatically, the entropy changes are
therefore small.
Looking at Fig. A.2, we see that the density structure of
the inner ![]()
![]() of the iron core is extremely similar in all
progenitors, correlated with only small differences in the electron
fraction
of the iron core is extremely similar in all
progenitors, correlated with only small differences in the electron
fraction
![]() (Fig. A.3). The central value of
(Fig. A.3). The central value of
![]() varies
only by 5% between the progenitors. In contrast, the entropy per
baryon s and infall velocity v exhibit differences of up to 40%. There is a general trend that |v| and s increase with the
ZAMS mass, while
varies
only by 5% between the progenitors. In contrast, the entropy per
baryon s and infall velocity v exhibit differences of up to 40%. There is a general trend that |v| and s increase with the
ZAMS mass, while
![]() decreases.
decreases.
Outside of the core, larger differences between the progenitors exist and are associated with the location of the interfaces between layers of different chemical composition and the density structure in these layers. In particular, the Fe-Si and the Si-O interfaces can have significant influence on the evolution of the supernova shock. The enclosed mass at which the interfaces are located differs strongly between the progenitors and increases non-monotonically with the ZAMS mass, see Table A.1. In most cases the composition changes discontinuously from the heavy to the lighter nucleus at the interfaces, but also a more gradual enrichment of a layer with elements of the neighboring shell is possible. In both cases the progenitor structure shows a more or less large entropy jump at the interfaces. For larger entropy jumps, which are underlined in Table A.1, also large steps occur in the density profile.
Table B.1:
Characteristic parameters of the 1D models for the phases of
collapse, prompt shock propagation, and neutrino burst.
![]() is the time between the moment when the collapsing core reaches a
central density of
is the time between the moment when the collapsing core reaches a
central density of
![]() and the moment of shock creation
(which is nearly identical with the time of core bounce),
i.e. the time when the entropy behind the shock first
reaches a value of
and the moment of shock creation
(which is nearly identical with the time of core bounce),
i.e. the time when the entropy behind the shock first
reaches a value of
![]() /by. The shock creation radius
/by. The shock creation radius
![]() and enclosed mass
and enclosed mass
![]() are defined by the
radial position where this happens.
The energy loss
are defined by the
radial position where this happens.
The energy loss
![]() via neutrinos during the collapse phase is evaluated by integrating
the total neutrino luminosity (for an observer at rest at
r=400 km) over time from the moment when the core reaches
via neutrinos during the collapse phase is evaluated by integrating
the total neutrino luminosity (for an observer at rest at
r=400 km) over time from the moment when the core reaches
![]() until the moment when the dip in the
until the moment when the dip in the
![]() luminosity is produced around 2.5 ms after shock
formation. We call the time when the velocities behind the shock
drop below
luminosity is produced around 2.5 ms after shock
formation. We call the time when the velocities behind the shock
drop below
![]() the end of the prompt shock propagation
phase. This time,
the end of the prompt shock propagation
phase. This time,
![]() ,
is measured relative to the moment
of shock creation. At the end of the prompt shock propagation phase,
the shock is at radius
,
is measured relative to the moment
of shock creation. At the end of the prompt shock propagation phase,
the shock is at radius
![]() and its enclosed mass is
and its enclosed mass is
![]() .
The time of the
.
The time of the
![]() burst,
burst,
![]() ,
is defined as the post-bounce time when
the
,
is defined as the post-bounce time when
the
![]() luminosity maximum is produced at the shock, which then
is located at the radius
luminosity maximum is produced at the shock, which then
is located at the radius
![]() and mass
and mass
![]() .
Finally, the energy emitted during the
prompt
.
Finally, the energy emitted during the
prompt
![]() burst is defined as the time-integrated
burst is defined as the time-integrated
![]() luminosity for the FWHM of the burst,
luminosity for the FWHM of the burst,
![]() ,
evaluated at 400 km for an observer at rest.
,
evaluated at 400 km for an observer at rest.
With the exception of Model n13, the collapse times from a core central
density of
![]() until bounce
differ only by 10-20% between the models, lying
between
until bounce
differ only by 10-20% between the models, lying
between ![]() 20 and
20 and ![]() 25 ms (see Fig. B.1
and Table B.1). In general, the results listed in Table B.1 and visible in Figs. A.3 and B.1-B.3
reveal an astonishing degree of convergence of the core evolution for
the different progenitors during the phases of collapse, shock
formation, prompt shock propagation and breakout
25 ms (see Fig. B.1
and Table B.1). In general, the results listed in Table B.1 and visible in Figs. A.3 and B.1-B.3
reveal an astonishing degree of convergence of the core evolution for
the different progenitors during the phases of collapse, shock
formation, prompt shock propagation and breakout
![]() burst (cf. also Liebendörfer et al. 2002).
Initially, the stellar cores differ in the amount of
deleptonization and have been evolved differently close to the onset of
collapse. Less deleptonized cores, however, need a longer time until the
collapse becomes dynamical (because their
burst (cf. also Liebendörfer et al. 2002).
Initially, the stellar cores differ in the amount of
deleptonization and have been evolved differently close to the onset of
collapse. Less deleptonized cores, however, need a longer time until the
collapse becomes dynamical (because their
![]() and thus electron
pressure are higher and photodisintegrations of Fe-group nuclei
proceed more slowly), thus allowing deleptonization to catch up with
that of the more evolved progenitors. Despite of remaining differences
at
and thus electron
pressure are higher and photodisintegrations of Fe-group nuclei
proceed more slowly), thus allowing deleptonization to catch up with
that of the more evolved progenitors. Despite of remaining differences
at
![]() (Figs. A.3 and B.2), the central quantities and radial profiles, in
particular of entropy and
(Figs. A.3 and B.2), the central quantities and radial profiles, in
particular of entropy and
![]() ,
become very similar after neutrino
trapping sets in at
,
become very similar after neutrino
trapping sets in at
![]() (Figs. B.2, B.3). This suggests a
strongly self-regulating character of the hydrodynamics coupled with
the neutrino transport, which ensures that the characteristic
properties of the homologous core at bounce are almost independent of
the initial conditions (Liebendörfer et al. 2002). Only Model s25a28 has such
a high value of the entropy and such a low value of
(Figs. B.2, B.3). This suggests a
strongly self-regulating character of the hydrodynamics coupled with
the neutrino transport, which ensures that the characteristic
properties of the homologous core at bounce are almost independent of
the initial conditions (Liebendörfer et al. 2002). Only Model s25a28 has such
a high value of the entropy and such a low value of
![]() at the time
when
at the time
when
![]() (Figs. A.3 and B.2) that both quantities do not fully converge to
those of the other
models. In this model the higher entropy implies that the EoS yields a
much larger free proton abundance, which leads to slightly stronger
deleptonization and thus a somewhat larger entropy (the entropy level
is higher by about
(Figs. A.3 and B.2) that both quantities do not fully converge to
those of the other
models. In this model the higher entropy implies that the EoS yields a
much larger free proton abundance, which leads to slightly stronger
deleptonization and thus a somewhat larger entropy (the entropy level
is higher by about
![]() )
after trapping
)
after trapping![]() .
.
As a consequence of the similar collapse
evolution, all models lose approximately the same amount of energy via
neutrino emission during collapse, i.e. around 1051 erg,
and because of the similar core structure and collapse history,
the shock in all cases is created at an enclosed mass of
![]() ,
corresponding to a radius
of
,
corresponding to a radius
of
![]() (Table B.1 and Fig. B.3a).
Following Bruenn & Mezzacappa (1997) we define the shock
creation (sc) time and location by the moment and position where the
entropy first reaches
(Table B.1 and Fig. B.3a).
Following Bruenn & Mezzacappa (1997) we define the shock
creation (sc) time and location by the moment and position where the
entropy first reaches
![]() per baryon.
From now on all times will be normalized to the time
of core bounce,
per baryon.
From now on all times will be normalized to the time
of core bounce,
![]() .
.
Also the prompt shock propagation is quite similar. In most models,
the velocities behind the shock become negative after 0.9 ms
(time
![]() in Table B.1) when the shock
encloses a mass of
in Table B.1) when the shock
encloses a mass of
![]() and has
reached a radius of
and has
reached a radius of
![]() (pse stands for "prompt shock
ends''). Only in case of the progenitors from Limongi et al. (2000) the
prompt shock pushes out a bit farther. It is interesting to note that
in all cases the stagnation of the shock happens earlier than the
(pse stands for "prompt shock
ends''). Only in case of the progenitors from Limongi et al. (2000) the
prompt shock pushes out a bit farther. It is interesting to note that
in all cases the stagnation of the shock happens earlier than the
![]() burst is released. The corresponding time
burst is released. The corresponding time
![]() in Table B.1 is defined as the
moment when the
in Table B.1 is defined as the
moment when the
![]() luminosity maximum is produced at the
shock
luminosity maximum is produced at the
shock![]() .
.
Although the prompt shock "stalls'' in the above defined sense, the
radial expansion velocity of the shock remains large, see
Fig. B.4, upper left panel, because of mass of the collapsing
star being accreted through the shock and accumulating on
the central, collapsed core. When the shock has passed the neutrinosphere
after 4 ms at a radius of 60-70 km (Table B.1),
the energy and lepton number drain
via neutrino emission in the
![]() burst reduces the thermal and
degeneracy pressure of the electrons in the accreted material, so that the
shock continues to expand more slowly. The strength of this neutrino
burst is very similar for all models, see Fig. B.4, lower left
panel (cf. also Kachelrieß et al. 2005).
burst reduces the thermal and
degeneracy pressure of the electrons in the accreted material, so that the
shock continues to expand more slowly. The strength of this neutrino
burst is very similar for all models, see Fig. B.4, lower left
panel (cf. also Kachelrieß et al. 2005).
Our models show that the four parameters which characterize the
subsequent quasi-stationary accretion phase, the mass accretion
rate through the shock,
![]() ,
the mass
,
the mass
![]() and radius
and radius
![]() of the proto-neutron star (PNS), and the neutrino
luminosity
of the proto-neutron star (PNS), and the neutrino
luminosity ![]() ,
are not independent but
coupled (Fig. B.4). The governing variable is
the time-dependent mass accretion rate through the shock, which is
determined by the progenitor structure. Since the mass accreted by the
shock is further advected onto the PNS with a small time delay, the
mass of the PNS is essentially the time integral of
,
are not independent but
coupled (Fig. B.4). The governing variable is
the time-dependent mass accretion rate through the shock, which is
determined by the progenitor structure. Since the mass accreted by the
shock is further advected onto the PNS with a small time delay, the
mass of the PNS is essentially the time integral of
![]() plus an
initial value. Starting at
plus an
initial value. Starting at
![]() ,
this
initial PNS mass is approximately
,
this
initial PNS mass is approximately
![]() for all models due to
the similar progenitor core structure. Also the neutrino luminosity
depends on
for all models due to
the similar progenitor core structure. Also the neutrino luminosity
depends on
![]() :
the gravitational binding energy of the accreted
matter must be radiated away when accretion proceeds in a stationary
way. The total neutrino luminosity therefore contains a part from
the cooling of the contracting core of the PNS (which loses its binding
energy over a timescale of about 10 s) plus a contribution from the settling
accretion layer, which is proportional to
:
the gravitational binding energy of the accreted
matter must be radiated away when accretion proceeds in a stationary
way. The total neutrino luminosity therefore contains a part from
the cooling of the contracting core of the PNS (which loses its binding
energy over a timescale of about 10 s) plus a contribution from the settling
accretion layer, which is proportional to
![]() with some lag,
because the material has to fall from the shock to the cooling
layer, where neutrinos are then released over a thermal cooling
timescale of some 10 ms. Interestingly, also the neutrinosphere radii
reveal a variability with
with some lag,
because the material has to fall from the shock to the cooling
layer, where neutrinos are then released over a thermal cooling
timescale of some 10 ms. Interestingly, also the neutrinosphere radii
reveal a variability with
![]() .
A large (small) accretion rate
leads to an approximately stationary solution with more (less) matter
piling up on the nascent neutron star before it can radiate away its
energy in form of neutrinos. Thus the PNS obtains a hot, extended
(cool, narrow) mantle with relatively high (low) densities and optical
depths, releasing neutrinos only on a longer (shorter) timescale. The
neutrinosphere therefore moves to a larger (smaller) radius
.
A large (small) accretion rate
leads to an approximately stationary solution with more (less) matter
piling up on the nascent neutron star before it can radiate away its
energy in form of neutrinos. Thus the PNS obtains a hot, extended
(cool, narrow) mantle with relatively high (low) densities and optical
depths, releasing neutrinos only on a longer (shorter) timescale. The
neutrinosphere therefore moves to a larger (smaller) radius ![]() in
case of mass accretion proceeding at high (low) rates
(Fig. B.4).
in
case of mass accretion proceeding at high (low) rates
(Fig. B.4).
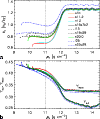 |
Figure B.2:
Central entropy (panel a)) and central electron and
lepton fraction (panel b)) versus central density during core collapse
for all 1D models. The vertical dotted line marks the time of
comparison at a central density
|
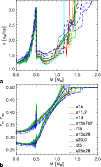 |
Figure B.3: Entropy (panel a)) and electron and lepton fraction (panel b)) versus enclosed mass at the time of shock formation. |
In summary, all the variables which determine the structure of
the postshock accretion layer depend on the time evolution of
![]() :
a high
:
a high
![]() leads to larger values of
leads to larger values of ![]() and
and ![]() ,
and a
faster increase of
,
and a
faster increase of
![]() .
Figure B.4 shows this
dependence. Looking, e.g., at
.
Figure B.4 shows this
dependence. Looking, e.g., at
![]() we see
that
we see
that
![]() varies by a factor of five between the models, being 0.8
and 1.3
varies by a factor of five between the models, being 0.8
and 1.3
![]() in case of Models n13 and s11.2,
respectively, at the low mass end of considered progenitors, and 3-4
in case of Models n13 and s11.2,
respectively, at the low mass end of considered progenitors, and 3-4
![]() for Models l25 and s25a28 at the high end of the
progenitor mass spectrum. Consistently,
for Models l25 and s25a28 at the high end of the
progenitor mass spectrum. Consistently, ![]() at
at
![]() is only 60 km for the low-mass progenitors and 25%
higher, i.e. about 80 km, for the high-mass models. Also the
luminosities differ by a factor of two, and the PNS masses show
differences of order 25%.
is only 60 km for the low-mass progenitors and 25%
higher, i.e. about 80 km, for the high-mass models. Also the
luminosities differ by a factor of two, and the PNS masses show
differences of order 25%.
The shock radius follows the time evolution of the neutron star radius
qualitatively, but with some time delay. Interestingly, during
phases of slowly changing
![]() the influence of different values of
the influence of different values of
![]() on the shock position is rather modest. The shock radii are
nearly identical for all progenitors until
on the shock position is rather modest. The shock radii are
nearly identical for all progenitors until ![]() 25 ms after bounce
and differ at most by about 10% until about 80 ms post-bounce. During
this phase, the significantly larger differences in
25 ms after bounce
and differ at most by about 10% until about 80 ms post-bounce. During
this phase, the significantly larger differences in
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() mentioned
above seem to partly
compensate each other in their influence on the shock radius. For
higher values of
mentioned
above seem to partly
compensate each other in their influence on the shock radius. For
higher values of
![]() the shock radius is smaller because of the
higher ram pressure. A larger
the shock radius is smaller because of the
higher ram pressure. A larger
![]() increases the
gravitational pull and thus also lowers
increases the
gravitational pull and thus also lowers
![]() .
But on the
other hand a higher
.
But on the
other hand a higher ![]() increases the heating and thus leads to an
expansion of the heating region, which is supported from below by a
larger PNS (because
increases the heating and thus leads to an
expansion of the heating region, which is supported from below by a
larger PNS (because ![]() is larger).
is larger).
Of course, the counteracting effects do not compensate each other
perfectly. As can be seen at later times, the shock radii differ more
strongly when the PNSs begin to show a wider spread in mass, although
with nearly the same radius, and in particular when the mass accretion
rates show differences of a factor of about 10 instead of the factor
of 2 at early times. The analytic study of Arcones Segovia (2003) and
Arcones & Janka (in preparation) reveals that the steady-state
accretion shock radius
is a sensitive function of the PNS radius (
![]() ), and decreases less strongly with higher mass
accretion rate and proto-neutron star mass (see also
Fryer et al. 1996).
), and decreases less strongly with higher mass
accretion rate and proto-neutron star mass (see also
Fryer et al. 1996).
A linear analysis is performed to determine the sensitivity of the PNS structure, i.e. contraction or expansion, to changes or redistribution of lepton number and energy in some layer. This analysis is then applied to the main effects of convective activity in the nascent neutron star, (1) the transport of lepton number and energy within the convective layer, and (2) the differences in the loss of lepton number and energy by neutrino emission in 2D simulations compared to 1D models.
We demonstrate the analysis in case of lepton number variations,
holding the specific internal energy fixed, but variations of the
internal energy can be investigated in the same way. Assuming
Newtonian gravity, which is sufficient here because we are interested
in qualitative, not quantitative results, the hydrostatic structure of
the PNS is determined by
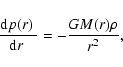 |
(C.1) |
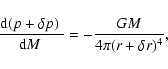 |
(C.5) |
Expanding the RHS to first order, inserting Eq. (C.4), and
subtracting Eq. (C.2) leads to
| |
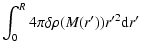 |
||
![$\displaystyle \left.\frac{\partial p}{\partial Y}\right\vert _\rho
(M_{\rm p}) ...
...ght\vert _Y
(M_{\rm p}) \right]^{-1} \cdot
\frac{m_{\rm by}}{\rho(M_{\rm p})} ,$](/articles/aa/full/2006/37/aa4654-05/img313.gif) |
(C.8) |
A relation between changes of mass and radius can be obtained by using
![]() .
Expanding to first order,
we thus get a relation between
.
Expanding to first order,
we thus get a relation between ![]() and
and
![]() :
:
In order to take into account the RHS of Eq. (C.6) we apply
an iterative procedure: The solution
![]() of iteration step i is inserted on the RHS of
Eq. (C.6), which is then numerically integrated over M to
find the solution
of iteration step i is inserted on the RHS of
Eq. (C.6), which is then numerically integrated over M to
find the solution
![]() .
In the first iteration step
the solution for
.
In the first iteration step
the solution for
![]() from Eq. (C.7) is used to
calculate
from Eq. (C.7) is used to
calculate
![]() from Eq. (C.9). We find that for
typical PNS profiles Eq. (C.7) provides a very good
approximation already; the next iteration step changes
from Eq. (C.9). We find that for
typical PNS profiles Eq. (C.7) provides a very good
approximation already; the next iteration step changes ![]() by 10-5 at most.
by 10-5 at most.
In Fig. C.1 we present the change of ![]() when one
electron or an energy of
when one
electron or an energy of
![]() is removed from the PNS at
different radii (or densities, corresponding to different enclosed
masses
is removed from the PNS at
different radii (or densities, corresponding to different enclosed
masses ![]() )
for two representative times in the evolution
of Model s15_32. Note that adding one electron or
)
for two representative times in the evolution
of Model s15_32. Note that adding one electron or
![]() would have
the opposite effect. We see that removing this amount of energy always
leads to contraction, while the extraction of one electron always
causes expansion of the PNS. The latter finding can be understood from
the fact that the electron is taken away but its degeneracy energy is
assumed to remain in the PNS as thermal energy.
would have
the opposite effect. We see that removing this amount of energy always
leads to contraction, while the extraction of one electron always
causes expansion of the PNS. The latter finding can be understood from
the fact that the electron is taken away but its degeneracy energy is
assumed to remain in the PNS as thermal energy.
When discussing the effects of the convective transport of energy and
lepton number on the PNS structure, it is interesting to
compare the values of ![]() in the drain region, where
in the drain region, where
![]() and
and
![]() drop, and in the dump region, where
drop, and in the dump region, where
![]() and
and
![]() increase due to convection. For example, at
increase due to convection. For example, at
![]() ,
the
removal of
,
the
removal of
![]() from the drain region will lead to an increase of
the mass enclosed by some large radius R by
from the drain region will lead to an increase of
the mass enclosed by some large radius R by
![]() g (Fig. C.1),
while adding these
g (Fig. C.1),
while adding these
![]() in the dump region will reduce
in the dump region will reduce
![]() by
by
![]() g (Fig. C.1).
This means a net decrease of
g (Fig. C.1).
This means a net decrease of
![]() ,
and thus an expansion of the PNS. This behaviour is also seen
at later times and in a similar way for the transport of
,
and thus an expansion of the PNS. This behaviour is also seen
at later times and in a similar way for the transport of
![]() .
.
In order to test the consequences of PNS convection on the PNS and supernova evolution in 1D simulations, we have developed a simple numerical "mixing algorithm'', which reproduces the energy and lepton number transport found in 2D models to a high degree.
In this algorithm we assume that any convective activity in the PNS
leads instantaneously to a redistribution of energy and lepton number
in the unstable region so that the convectively unstable gradients
disappear, i.e.
![]() is established.
Setting
is established.
Setting
![]() and assuming
and assuming
![]() in
Eq. (7), we find that the instability is mainly
driven by a negative gradient of the entropy (including neutrino
entropy).
in
Eq. (7), we find that the instability is mainly
driven by a negative gradient of the entropy (including neutrino
entropy).
![]() then corresponds to a flat entropy
profile, consistent with what is observed in
the PNS convective region in 2D simulations, see
Figs. 9 and 10.
The numerical mixing scheme redistributes the energy in an unstable
layer in a conservative way such that the entropy profile develops
a plateau.
then corresponds to a flat entropy
profile, consistent with what is observed in
the PNS convective region in 2D simulations, see
Figs. 9 and 10.
The numerical mixing scheme redistributes the energy in an unstable
layer in a conservative way such that the entropy profile develops
a plateau.
As a second constraint we introduce the empirically derived relation
The mixing algorithm is executed in an operator splitting step after
each hydrodynamic step. The algorithm detects regions with a negative
entropy (![]() )
gradient inside the PNS. In these regions
energy and lepton number are then redistributed in such a way that
Eq. (D.1),
)
gradient inside the PNS. In these regions
energy and lepton number are then redistributed in such a way that
Eq. (D.1),
![]() ,
and
global energy and lepton number conservation are fulfilled (GR gravitational effects are ignored).
,
and
global energy and lepton number conservation are fulfilled (GR gravitational effects are ignored).
We find empirically that for ![]() the evolution of the profiles
of
the evolution of the profiles
of
![]() ,
,
![]() ,
and
,
and
![]() inside the PNS for
simulations with the mixing scheme reproduce very well the results of
the 2D model, see Fig. 10. Near the boundaries of
the convectively unstable layer small differences can appear. The
over- and undershooting of dynamically moving matter into convectively
stable layers can, of course, not be properly accounted for by this simple
scheme. Another deficiency of the scheme is best visible shortly after
the onset
of convection around 50 ms after bounce, when the Brunt-Vaisälä
frequency can reach values of up to 2 ms-1 (Figs. 9
and D.1, panel b), and the convective
layer has not yet fully developed and the transient starting
phase with growing perturbations is not yet over. In this nonstationary,
early phase of PNS convection the results with the mixing scheme
cannot reproduce the
inside the PNS for
simulations with the mixing scheme reproduce very well the results of
the 2D model, see Fig. 10. Near the boundaries of
the convectively unstable layer small differences can appear. The
over- and undershooting of dynamically moving matter into convectively
stable layers can, of course, not be properly accounted for by this simple
scheme. Another deficiency of the scheme is best visible shortly after
the onset
of convection around 50 ms after bounce, when the Brunt-Vaisälä
frequency can reach values of up to 2 ms-1 (Figs. 9
and D.1, panel b), and the convective
layer has not yet fully developed and the transient starting
phase with growing perturbations is not yet over. In this nonstationary,
early phase of PNS convection the results with the mixing scheme
cannot reproduce the
![]() -profiles of the 2D simulations
very well (Fig. D.1, panel a); lepton number is
transported more efficiently in the 2D models.
-profiles of the 2D simulations
very well (Fig. D.1, panel a); lepton number is
transported more efficiently in the 2D models.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4654f12b.eps}
\end{figure}](/articles/aa/full/2006/37/aa4654-05/Timg338.gif) |
Figure E.2:
Standard deviations of the density fluctuations in lateral direction,
|
The majority of our models were computed through the phases of core collapse, bounce, shock formation, and shock stagnation in spherical symmetry, and then continued in 2D with random perturbations added during the mapping from the 1D to the 2D grid. In contrast, we followed the evolution of Models s15_64_p and s15_64_r in two dimensions also during core collapse, shock formation, and early shock propagation. In this case the spherically symmetric density structure of the progenitor core was perturbed in each cell of the computational grid in a random way, in case of Model s15_64_p with an amplitude of 2%, in Model s15_64_r with 1% amplitude (Table 1). We will discuss here briefly the evolution of the perturbations during the core collapse phase, concentrating on Model s15_64_p. Since the initial spin is too low, rotation hardly affects the pre-bounce evolution of Model s15_64_r, and the latter model does not show any important rotation-induced differences with respect to the perturbation growth. When running the simulations continuously in 2D instead of mapping 1D post-bounce models on a 2D grid some milliseconds after bounce, we detect a slightly earlier onset of convection, which is seeded by the density and velocity fluctuations in the convectively unstable layers that develop below the neutrinosphere and in the neutrino-heating layer behind the stalled shock. Despite the earlier start of convection behind the shock, no significant differences of the evolution could be discovered between Models s15_32 and s15_64_p (Figs. 11-17). We therefore have included the results of the latter model in the relevant plots in Sect. 3, but have not specifically discussed them in the text.