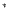 Models s112_32, s112_64, s15_32, s15_64_p, s15_64_r, and
s20_32 were discussed in overview in Buras et al. (2003).
Models s112_32, s112_64, s15_32, s15_64_p, s15_64_r, and
s20_32 were discussed in overview in Buras et al. (2003).
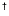 This is Model s15Gio_32.b from Buras et al. (2006).
Different from the other models presented in this paper, Model s15_32
was computed with an older implementation of the gravitational potential,
which contained a slightly different treatment of the relativistic
corrections in the potential (see also the comment in Table B.1).
This affects only the neutrino luminosities
and average neutrino energies by a few percent. We have corrected
this difference in our plots for the luminosities and mean energies. The
correction was calculated as
This is Model s15Gio_32.b from Buras et al. (2006).
Different from the other models presented in this paper, Model s15_32
was computed with an older implementation of the gravitational potential,
which contained a slightly different treatment of the relativistic
corrections in the potential (see also the comment in Table B.1).
This affects only the neutrino luminosities
and average neutrino energies by a few percent. We have corrected
this difference in our plots for the luminosities and mean energies. The
correction was calculated as
 ,
where ,
where
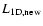 and
and
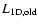 are the luminosities of the 1D simulations with
the "new'' and "old'' versions of the gravitational potential,
respectively. Then the corrected luminosity is given by
are the luminosities of the 1D simulations with
the "new'' and "old'' versions of the gravitational potential,
respectively. Then the corrected luminosity is given by
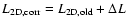 ,
where ,
where
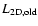 is the
luminosity of the 2D model which was simulated with the old version
of the gravitational potential. For the average neutrino energies
the procedure is analogous.
is the
luminosity of the 2D model which was simulated with the old version
of the gravitational potential. For the average neutrino energies
the procedure is analogous.
 This model was calculated in 1D using the mixing
algorithm described in Appendix D for treating
effects from PNS convection.
This model was calculated in 1D using the mixing
algorithm described in Appendix D for treating
effects from PNS convection. |