Appendices are only available in electronic form at http://www.edpsciences.org

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

Present address: Rechenzentrum der Max-Planck-Gesellschaft am Max-Planck-Institut für Plasmaphysik, Boltzmannstr. 2, 85748 Garching, Germany.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... EoS

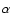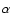The error in the $\alpha$ -particle mass fraction that was recently discoved in the EoS of Lattimer & Swesty (1991) was tested to have no important influence on our simulations; for details see Buras et al. (2006). In some models, we replaced the Lattimer & Swesty EoS below a density of 10¹¹ g cm^-3, i.e. in the regime of possible $\alpha$ -particle presence after bounce, by our low-density EoS without discovering any significant dynamical differences.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... (PNS)

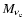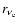For simplicity, we identify the PNS mass and radius with the mass and radius enclosed by the electron neutrinosphere, $M_{\nu_{\rm e}}$ and $r_{\nu_{\rm e}}$ , respectively. Throughout this paper, neutrinospheres are defined as "transport spheres'', using the opacities for momentum transfer between neutrinos and stellar medium in calculating optical depths, as given in Eq. (28) of Buras et al. (2006).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

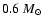
... $0.6~\ensuremath{M_{\odot}}$

Note that in 2D simulations the "enclosed mass'' is not a Lagrangian coordinate but corresponds to the sphere which contains a certain amount of mass at a given time.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... level

The large values of $E_{\rm kin,lat}$ between the neutrinosphere and the gain radius in case of Model s112_64, which can be inferred from Fig. 23, are a consequence of our choice of periodic boundary conditions at both lateral boundaries of the 90 $\hbox{$^\circ$ }$ wedge used in this model, see Sect. 3.1.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... failure

In this context it is interesting to note that for an 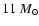$11~M_\odot$ progenitor from Woosley et al. (2002), which has a less steep density profile exterior to the iron core, Burrows et al. (2006) did not find an explosion before about 0.5 s after bounce. Besides a different progenitor, there were, however, also other differences. They, e.g., performed purely Newtonian simulations and used a flux-limited diffusion treatment for the neutrino transport, in which energy bin coupling by Doppler shifts and neutrino-electron scattering were ignored.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... exists

The Monte Carlo calculations by Janka & Mönchmeyer (1989b) did not make use of such simplifications, assumed, however, that the transport in different lateral directions of the 2D environment can be approximated by a "ray-by-ray'' approach, in which the neutrino flux at a given latitude is assumed to be radial and can be calculated by the transport in a spherical background with a radial structure as it is present in the 2D model at this latitude.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... trapping

Note that the small differences in 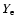${Y_{\rm e}}$ and in 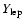${Y_{\rm lep}}$ after trapping disappear completely, and those in entropy remain slightly larger, when the simulations are done with the sophisticated implementation of electron captures on nuclei of Langanke et al. (2003).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... shock

Technically this moment is determined by taking the time of maximum luminosity at 400 km minus the time of flight between the neutrinosphere and this radius.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.