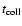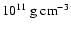Table B.1: Characteristic parameters of the 1D models for the phases of collapse, prompt shock propagation, and neutrino burst. $t_{\rm coll}$ is the time between the moment when the collapsing core reaches a central density of  $10^{11}~\ensuremath{{\rm g}~{\rm cm}^{-3}} $ and the moment of shock creation (which is nearly identical with the time of core bounce), i.e. 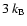the time when the entropy behind the shock first reaches a value of  $3~\ensuremath{k_{\rm B}} $/by. The shock creation radius 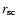 $r_{\rm sc}$ and enclosed mass 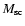 $M_{\rm sc}$ are defined by the radial position where this happens. 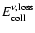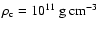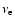The energy loss $E_{\rm coll}^{\nu ,{\rm loss}}$ via neutrinos during the collapse phase is evaluated by integrating the total neutrino luminosity (for an observer at rest at r=400 km) over time from the moment when the core reaches $\rho_{\rm c} = 10^{11}~\ensuremath{{\rm g}~{\rm cm}^{-3}} $ until the moment when the dip in the $\nu _{{\rm e}}$ luminosity is produced around 2.5 ms after shock formation. 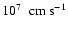We call the time when the velocities behind the shock drop below $10^7~~\ensuremath{{\rm cm}~{\rm s}^{-1}} $ the end of the prompt shock propagation phase. 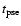This time, $t_{\rm pse}$, is measured relative to the moment of shock creation. 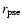At the end of the prompt shock propagation phase, the shock is at radius $r_{\rm pse}$ and its enclosed mass is 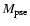$M_{\rm pse}$. 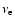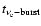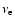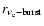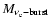The time of the $\nu _{{\rm e}}$ burst, $t_{{\nu _{\rm e}}-{\rm burst}}$, is defined as the post-bounce time when the $\nu _{{\rm e}}$ luminosity maximum is produced at the shock, which then is located at the radius $r_{{\nu _{\rm e}}-{\rm burst}}$ and mass $M_{{\nu _{\rm e}}-{\rm burst}}$. Finally, the energy emitted during the prompt 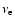$\nu _{{\rm e}}$ burst is defined as the time-integrated 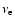$\nu _{{\rm e}}$ luminosity for the FWHM of the burst, 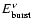$E_{\rm burst}^\nu $, evaluated at 400 km for an observer at rest.

Model 	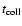	 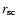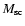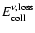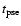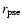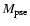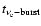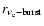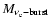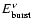$t_{\rm coll}$ $r_{\rm sc}$ $M_{\rm sc}$ $E_{\rm coll}^{\nu ,{\rm loss}}$ $t_{\rm pse}$ $r_{\rm pse}$ $M_{\rm pse}$ $t_{{\nu _{\rm e}}-{\rm burst}}$ $r_{{\nu _{\rm e}}-{\rm burst}}$ $M_{{\nu _{\rm e}}-{\rm burst}}$ $E_{\rm burst}^\nu $
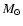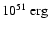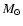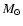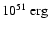  [ms] [km] [ $\ensuremath{M_{\odot}} $] [ $10^{51}~{\rm erg}$] [ms] [km] [ $\ensuremath{M_{\odot}} $] [ms] [km] [ $\ensuremath{M_{\odot}} $] [ $10^{51}~{\rm erg}$]
s1b 23.9 10.7 0.49 1.00 0.87 32 0.78 3.8 64 1.00 1.48
s11.2 25.2 10.7 0.50 1.00 0.87 32 0.78 3.7 63 1.00 1.38
n13 28.9 10.7 0.50 0.96 0.88 32 0.78 3.7 61 0.98 1.29
s15s7b2 $^\dagger$ 23.9 10.7 0.49 1.01 0.91 32 0.78 3.8 64 1.00 1.47
l15 20.9 10.6 0.50 1.04 1.03 35 0.82 4.1 68 1.04 1.74
s15a28 21.6 10.7 0.49 1.03 0.95 33 0.79 4.0 66 1.02 1.60
s20.0 22.7 10.6 0.49 1.03 0.91 32 0.79 3.8 64 1.01 1.50
l25 20.0 10.7 0.49 1.06 1.15 37 0.83 4.1 68 1.03 1.82
s25a28 19.8 10.6 0.48 1.06 1.00 34 0.79 4.1 68 1.03 1.93
$^\dagger$ This model is identical with Model s15Gio_1d.b in Buras et al. (2006) except for a slightly different, improved implementation of the relativistic corrections to the gravitational potential. This difference causes only small changes in the neutrino luminosities of a few percent, but otherwise has no visible consequences.

Source LaTeX | All tables | In the text