

Up: On the radio afterglow bursts
Subsections
We argue that the self-attenuation in the CB of the observed radio waves is
dominated by free-free absorption.
In the rest system of a CB, the ISM electrons arrive at a rate
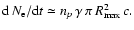 A fraction
A fraction 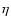 of their energy,
of their energy,
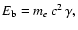 is
synchrotron
re-radiated. Let
is
synchrotron
re-radiated. Let
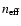 be the density of the emitting
electrons, so that:
be the density of the emitting
electrons, so that:
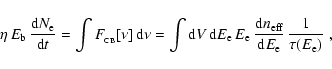 |
(46) |
with
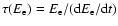 the cooling time for electrons
of energy Ee, determined from Eqs. (2) and
(10) to be:
the cooling time for electrons
of energy Ee, determined from Eqs. (2) and
(10) to be:
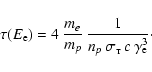 |
(47) |
For the electron spectrum of Eq. (13), the second integral
in Eq. (46) is dominated by energies
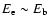 (
(
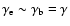 ). Thus, for a uniform distribution
of electrons in the CB's volume V, we obtain:
). Thus, for a uniform distribution
of electrons in the CB's volume V, we obtain:
where we have used our reference
 .
This density could be somewhat
higher if the emitting electrons are concentrated on the CB's front surface.
Note that this density increases with time like
.
This density could be somewhat
higher if the emitting electrons are concentrated on the CB's front surface.
Note that this density increases with time like
![$[\gamma(t)]^{-2}$](/articles/aa/full/2003/13/aa2654/img334.gif) .
.
For a power-law distribution,
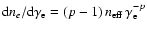 ,
the correct attenuation coefficient for synchrotron self absorption
at frequency
,
the correct attenuation coefficient for synchrotron self absorption
at frequency  is
(e.g., Shu 1991, Eqs. (19.37), (38)):
is
(e.g., Shu 1991, Eqs. (19.37), (38)):
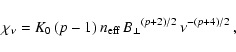 |
(49) |
where:
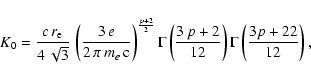 |
(50) |
with
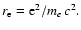 An observed frequency
An observed frequency
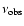 was emitted at
was emitted at
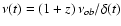 in
the CB's rest frame. As an example,
in
the CB's rest frame. As an example,
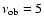 GHz
from a decelerating CB with
GHz
from a decelerating CB with
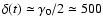 ,
if emitted at a typical
z=1, corresponds to
,
if emitted at a typical
z=1, corresponds to 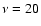 MHz in the CB rest frame.
For our reference parameters, the synchrotron
self absorption coefficient in the CB is
MHz in the CB rest frame.
For our reference parameters, the synchrotron
self absorption coefficient in the CB is
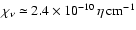 .
Since
.
Since
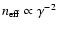 ,
,
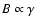 ,
and, after a few observer's days,
,
and, after a few observer's days,
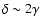 and
and
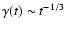 ,
,
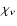 decreases
with time like
decreases
with time like
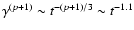 .
.
The X-ray AG is dominated first by bremsstrahlung from plasma
electrons and later by synchrotron radiation from the swept up high
energy electrons (DDD 2001). The observed X-ray flux, or the
theoretical UV flux in the CB rest frame, can be used to show that
the CB is partially ionized during the radio AG observations and
that the ionized fraction of the CB plasma is proportional to 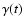 (see Appendix C). The logarithmic dependence of the
plasma temperature in the Saha equation on the fractional ionization,
keeps the CB's temperature nearly constant during its AG phase.
Consequently, in the CB rest frame, the free-free attenuation at
a fixed frequency is proportional to
(see Appendix C). The logarithmic dependence of the
plasma temperature in the Saha equation on the fractional ionization,
keeps the CB's temperature nearly constant during its AG phase.
Consequently, in the CB rest frame, the free-free attenuation at
a fixed frequency is proportional to
![$[\gamma(t)]^2$](/articles/aa/full/2003/13/aa2654/img351.gif) and the
free-free (bremsstrahlung) absorption coefficient is that of
Eq. (20).
and the
free-free (bremsstrahlung) absorption coefficient is that of
Eq. (20).
The temperature of the partially ionized CB is of
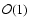 eV and almost constant during the observed AG. For
eV and almost constant during the observed AG. For 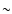 20 MHz
emission from a thermal plasma at such temperature,
20 MHz
emission from a thermal plasma at such temperature, 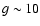 and for one tenth of the typical bulk CB density,
and for one tenth of the typical bulk CB density,
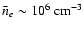 ,
one obtains from Eq. (20)
,
one obtains from Eq. (20)
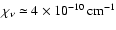 ,
which is
,
which is 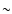
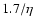 larger than the synchrotron absorption coefficient of
the energetic electrons in the CB (the values of
larger than the synchrotron absorption coefficient of
the energetic electrons in the CB (the values of 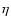 are listed
in Table 3). At a fixed observer frequency,
are listed
in Table 3). At a fixed observer frequency,
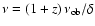 ,
the free-free opacity of the CB decreases roughly
like
,
the free-free opacity of the CB decreases roughly
like 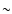
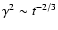 compared with the
compared with the 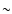 t-1.1 decline of the synchrotron self opacity.
t-1.1 decline of the synchrotron self opacity.
The conclusion is that free-free absorption is dominant for
as long as the ionization of the CB is considerable.


Up: On the radio afterglow bursts
Copyright ESO 2003
![]() A fraction
A fraction ![]() of their energy,
of their energy,
![]() is
synchrotron
re-radiated. Let
is
synchrotron
re-radiated. Let
![]() be the density of the emitting
electrons, so that:
be the density of the emitting
electrons, so that:
![]() eV and almost constant during the observed AG. For
eV and almost constant during the observed AG. For ![]() 20 MHz
emission from a thermal plasma at such temperature,
20 MHz
emission from a thermal plasma at such temperature, ![]() and for one tenth of the typical bulk CB density,
and for one tenth of the typical bulk CB density,
![]() ,
one obtains from Eq. (20)
,
one obtains from Eq. (20)
![]() ,
which is
,
which is ![]()
![]() larger than the synchrotron absorption coefficient of
the energetic electrons in the CB (the values of
larger than the synchrotron absorption coefficient of
the energetic electrons in the CB (the values of ![]() are listed
in Table 3). At a fixed observer frequency,
are listed
in Table 3). At a fixed observer frequency,
![]() ,
the free-free opacity of the CB decreases roughly
like
,
the free-free opacity of the CB decreases roughly
like ![]()
![]() compared with the
compared with the ![]() t-1.1 decline of the synchrotron self opacity.
t-1.1 decline of the synchrotron self opacity.