The ISM nuclei (mainly protons) that a CB scatters also decelerate its
flight: its Lorentz factor, ![]() ,
is calculable. Travelling at
a large
,
is calculable. Travelling at
a large ![]() and viewed at a small angle
and viewed at a small angle ![]() ,
the CB's emissions
are strongly relativistically aberrant: in minutes of observer's time,
the CBs are parsecs away from their source. For a constant CB radius and
an approximately constant ISM density,
,
the CB's emissions
are strongly relativistically aberrant: in minutes of observer's time,
the CBs are parsecs away from their source. For a constant CB radius and
an approximately constant ISM density, ![]() has an explicit
analytical expression, as discussed in Appendix A. Typically
has an explicit
analytical expression, as discussed in Appendix A. Typically
![]() at a distance of order 1 kpc from the source, and
at a distance of order 1 kpc from the source, and
![]() .
Due to a limited observational sensitivity, GRBs
have been detected only up to angles
.
Due to a limited observational sensitivity, GRBs
have been detected only up to angles ![]() of a few times
of a few times
![]() .
.
The ISM electrons entering a CB are caught up and bounce off
its enclosed magnetic domains acquiring a predictable power-law energy
spectrum, as we argue in Sect. 3. In the CB's rest system
![]() below an energy
below an energy
![]() ,
steepening to
,
steepening to
![]() ,
with
,
with
![]() ,
above this energy
,
above this energy![]() .
The energy
.
The energy ![]() does not correspond to the conventional
synchrotron ``cooling break'' but to the injection bend at the
energy at which electrons enter the CB with a Lorentz factor
does not correspond to the conventional
synchrotron ``cooling break'' but to the injection bend at the
energy at which electrons enter the CB with a Lorentz factor ![]() .
In Sect. 4 we discuss the observational
support of the existence of the injection bend, which is strong.
Given the very large magnetic and radiation energy densities
in the CB, the usual cooling break (at the energy at which
the energy-loss rate due to synchrotron emission and inverse Compton
scattering equals that due to bremsstrahlung,
adiabatic losses and escape) happens only at subrelativistic energies,
as discussed in Appendix B.
The magnetic energy-density in a CB (DDD 2001) is:
.
In Sect. 4 we discuss the observational
support of the existence of the injection bend, which is strong.
Given the very large magnetic and radiation energy densities
in the CB, the usual cooling break (at the energy at which
the energy-loss rate due to synchrotron emission and inverse Compton
scattering equals that due to bremsstrahlung,
adiabatic losses and escape) happens only at subrelativistic energies,
as discussed in Appendix B.
The magnetic energy-density in a CB (DDD 2001) is:
![\begin{displaymath}\nu\,{{\rm d}n_\gamma\over {\rm d}\,\nu} \propto
f_{\rm sync...
...{\rm b}(t)]^{-1/2}\over
\sqrt{1+[\nu/\nu_{\rm b}(t)]^{(p-1)}}}
\end{displaymath}](/articles/aa/full/2003/13/aa2654/img32.gif)
For the first ![]() 103 s of observer's time,
a CB is still cooling fast and emitting
via thermal bremsstrahlung (DDD 2001), but after that
the CB emissivity integrated over frequency is
equal to the energy deposition rate of the ISM
electrons in the CB
103 s of observer's time,
a CB is still cooling fast and emitting
via thermal bremsstrahlung (DDD 2001), but after that
the CB emissivity integrated over frequency is
equal to the energy deposition rate of the ISM
electrons in the CB![]() :
:
An observer in the GRB progenitor's rest system,
viewing a CB at an angle ![]() (corresponding to
(corresponding to
![]() in the CB's proper frame), sees its radiation
Doppler-boosted by a factor
in the CB's proper frame), sees its radiation
Doppler-boosted by a factor ![]() :
:
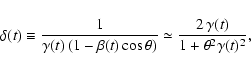
In DDD 2001 we fit, in the CB model, the R-band AG light curves of
GRBs. The fit involves five parameters per GRB:
the overall normalization; ![]() :
the viewing angle;
:
the viewing angle; ![]() :
the t=0 value of the
Lorentz factor;
:
the t=0 value of the
Lorentz factor; ![]() :
the ``deceleration''
parameter of the CBs in the ISM; and the
spectral index p. The value of p, obtained
from the temporal shape of the afterglow, is in every case
very close to the expectation p=2.2, and - within
the often large uncertainties induced by absorption - with
the observed spectra from optical frequencies to X-rays (DDD 2001).
:
the ``deceleration''
parameter of the CBs in the ISM; and the
spectral index p. The value of p, obtained
from the temporal shape of the afterglow, is in every case
very close to the expectation p=2.2, and - within
the often large uncertainties induced by absorption - with
the observed spectra from optical frequencies to X-rays (DDD 2001).
In this paper we complete our previous work by making broad-band
fits to the data at all available radio and optical frequencies.
In so doing, we need to introduce just one new ``radio''
parameter: an ``absorption frequency'' ![]() ,
corresponding
to unit CB opacity at a reference frequency. We set p=2.2 so
that the extension to a broad-band analysis does not involve an
increase in the total number of parameters. We have to refer very
often to the values of the parameters that our previous experience
with the CB model made us choose as reference values. For convenience,
these are listed in Table 1.
,
corresponding
to unit CB opacity at a reference frequency. We set p=2.2 so
that the extension to a broad-band analysis does not involve an
increase in the total number of parameters. We have to refer very
often to the values of the parameters that our previous experience
with the CB model made us choose as reference values. For convenience,
these are listed in Table 1.
The predictions of the CB model, for typical parameters,
are summarized in Fig. 1. The energy density spectra
at radio to optical frequencies are shown, at various times after
the GRB, in the upper panel. The spectral slopes before and soon after
the peak frequency are ![]() and -(p-1)/2, as indicated.
The spectra peak at a frequency at which self-attenuation in the CBs
results in an opacity of
and -(p-1)/2, as indicated.
The spectra peak at a frequency at which self-attenuation in the CBs
results in an opacity of ![]() (1).
At frequencies well above the frequency
(1).
At frequencies well above the frequency ![]() characterizing
the injection bend, the spectrum steepens to a slope -p/2.
In the figure's lower panel
we show light curves at various radio frequencies. At large times
and for
characterizing
the injection bend, the spectrum steepens to a slope -p/2.
In the figure's lower panel
we show light curves at various radio frequencies. At large times
and for
![]() - which is the case at all frequencies
in the example of Fig. 1, whose parameters
are close to those of GRB 000301c - they
tend to
- which is the case at all frequencies
in the example of Fig. 1, whose parameters
are close to those of GRB 000301c - they
tend to
![]() ,
this behaviour being reached
at earlier times, the higher the frequency.
For
,
this behaviour being reached
at earlier times, the higher the frequency.
For
![]() ,
the corresponding limiting behaviour
is
,
the corresponding limiting behaviour
is ![]() t-4/3, observable at low frequencies
in the cases of GRBs 991216, 991208 and 000418. All of the above
predictions are robust: they do not depend on the
detailed form of the attenuation, cumulation and limb-darkening
factors. The early rise
of the light curves does depend on such details, on which
we shall have to invest a disproportionate effort in Sects. 5 to 7.
t-4/3, observable at low frequencies
in the cases of GRBs 991216, 991208 and 000418. All of the above
predictions are robust: they do not depend on the
detailed form of the attenuation, cumulation and limb-darkening
factors. The early rise
of the light curves does depend on such details, on which
we shall have to invest a disproportionate effort in Sects. 5 to 7.
The CB model provides an excellent description of the data, as discussed in Sects. 4, 8 and 9. In the case of GRB 980425, for which the optical AG is dominated by SN1998bw, we used the parameters that fit its X-ray afterglow (DDD 2001) and the GRB's fluence (Dar & De Rújula 2000a) to argue that they are not exceptional. The CB-model's description of the radio data for this GRB/SN pair is excellent: there is nothing peculiar about this GRB, nor about its associated supernova, as we discuss in detail in Sect. 9, along with the question of the angular separation in the sky of the SN and the associated CBs, which may have been, or may still be, observable.
The apparent sky velocities of cosmological CBs are extremely superluminal and their angular velocities happen to be of the same order of magnitude as those of galactic pulsars. This implies that CB velocities can possibly be extracted from their observed radio scintillations, as discussed in Sect. 12.
Copyright ESO 2003