The acceleration of charged particles by a moving CB is not substantially different from some of the cases already studied in the literature, the acceleration of cosmic rays and electrons having attracted an enormous amount of attention since Fermi's first analysis in 1949 (for an excellent introduction, see Longair 1994). The most efficient and thus promising mechanism is the ``first-order'' acceleration of particles by fast-moving shocks, extensively studied analytically and numerically since the pioneering works of Axford et al. (1977), Krymsky (1977), Bell (1978) and Blandford & Ostriker (1978). The analysis closest to the case at hand is that of Ballard & Heavens (1992), who studied acceleration by relativistic shocks, with the charged particles deflected by highly disordered magnetic fields, rather than, as it is generally assumed, by small irregularities in an otherwise uniform field. The ``relativistic'' and ``chaotic'' inputs are what make this work particularly relevant to the case of particle acceleration by and within CBs.
Ballard and Heavens study numerically, for various values of a
moving discontinuity's Lorentz factor ranging up to
![]() ,
the result of its collision with an isotropic ensemble of particles
with
,
the result of its collision with an isotropic ensemble of particles
with
![]() .
They find that, for
.
They find that, for
![]() ,
the resulting particle energy distribution has a break (in this reference
system) at
,
the resulting particle energy distribution has a break (in this reference
system) at
![]() ,
at which point it steepens.
The particles below the break have a dominantly
very forward motion: they are the ones which have been upscattered
just once. Given this hint, it is easy to reproduce the numerical
results in an analytic approximation. In the shock's rest system,
the energy of the particles that have been scattered only once
is equal to their incoming energy: the break in the spectrum
seen in the simulations is a kinematical break occurring roughly
at the injection energy. ``Observed'' in the system in which the
shock is travelling at
,
at which point it steepens.
The particles below the break have a dominantly
very forward motion: they are the ones which have been upscattered
just once. Given this hint, it is easy to reproduce the numerical
results in an analytic approximation. In the shock's rest system,
the energy of the particles that have been scattered only once
is equal to their incoming energy: the break in the spectrum
seen in the simulations is a kinematical break occurring roughly
at the injection energy. ``Observed'' in the system in which the
shock is travelling at
![]() ,
this injection bend
is very reminiscent of the familiar synchrotron-cooling ``break'',
but it has little to do with it; indeed, in the simulations of Ballard &
Heavens (1992) cooling was entirely neglected.
,
this injection bend
is very reminiscent of the familiar synchrotron-cooling ``break'',
but it has little to do with it; indeed, in the simulations of Ballard &
Heavens (1992) cooling was entirely neglected.
Consider the CB in its rest system and temporarily postpone the
discussion of cooling. The ISM electrons impinge on the CB in a fixed direction
with a Lorentz factor equal to that of the CB in the GRB progenitor's rest system,
![]() .
The electrons not having ``bounced back''
off the CB's strong magnetic field, or having
done it only once, retain the incoming energy,
.
The electrons not having ``bounced back''
off the CB's strong magnetic field, or having
done it only once, retain the incoming energy,
![]() ,
so that their energy distribution is:
,
so that their energy distribution is:
![]() .
A very robust (i.e. detail independent) feature of the studies
of acceleration by relativistic shocks is that the particles
having bounced more than once acquire a spectrum
.
A very robust (i.e. detail independent) feature of the studies
of acceleration by relativistic shocks is that the particles
having bounced more than once acquire a spectrum
![]() ,
with p=2 in analytical approximations and
,
with p=2 in analytical approximations and ![]() in numerical simulations. A few bounces are sufficient to attain
such a spectrum. The CB is a system of finite transverse dimensions
and the magnetic field contrast between its interior and its exterior
is very large. Thus, we do not expect the same electron to bounce
many times off the CB, as the latter catches up with it. The
acceleration should occur mainly within the CB as charged particles
bounce off its chaotically moving magnetic domains, and it should be very
fast and efficient, since the injection is highly relativistic and
there is no distinction between ``first and second order Fermi'' processes.
The overall ``source''
spectrum of relativistic electrons is:
in numerical simulations. A few bounces are sufficient to attain
such a spectrum. The CB is a system of finite transverse dimensions
and the magnetic field contrast between its interior and its exterior
is very large. Thus, we do not expect the same electron to bounce
many times off the CB, as the latter catches up with it. The
acceleration should occur mainly within the CB as charged particles
bounce off its chaotically moving magnetic domains, and it should be very
fast and efficient, since the injection is highly relativistic and
there is no distinction between ``first and second order Fermi'' processes.
The overall ``source''
spectrum of relativistic electrons is:
The electron energy loss by synchrotron radiation is:
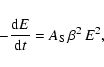
Copyright ESO 2003