

Up: On the radio afterglow bursts
We argue that the synchrotron radiation in a CB is intense
enough to maintain its plasma partially ionized with ion and
free electron densities proportional to 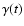 .
.
The bound-free cross section for photoionization of atomic hydrogen in its nth excited state by photons with frequency above the ionization
threshold,
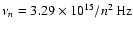 ,
is given by
,
is given by
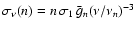 ,
with
,
with
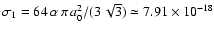 cm2 (
cm2 (
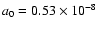 cm
is the Bohr radius
and
cm
is the Bohr radius
and 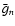 is the Gaunt factor
for photoabsorption by hydrogen).
For the surface flux of photons of Eq. (6), we obtain
an ionization rate of the nth level of atomic hydrogen:
is the Gaunt factor
for photoabsorption by hydrogen).
For the surface flux of photons of Eq. (6), we obtain
an ionization rate of the nth level of atomic hydrogen:
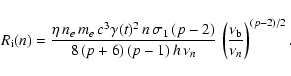 |
(44) |
For the reference values of ne, p and
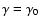 ,
the ionization rate of
the ground state is
,
the ionization rate of
the ground state is
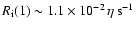 .
.
The recombination rate per unit volume
of hydrogen in an hydrogenic CB is (Osterbrock
1989):
![\begin{displaymath}R_{\rm rec}\simeq 1.0\times 10^{-12}\,\bar n_{e}\,
\left[{T\over 10^4\,{\rm K}}\right]^{-0.7}\,{\rm s}^{-1} .
\end{displaymath}](/articles/aa/full/2003/13/aa2654/img318.gif) |
(45) |
For the reference value of the CB parameters, and
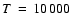 K the recombination rate of hydrogen is
K the recombination rate of hydrogen is
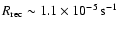 .
In quasi equilibrium, the ionization rate per unit
volume, which is proportional to the number density of recombined hydrogen
atoms, must be equal to the recombination rate per unit volume, which is
proportional to the product of the ion and free electron densities in the
CB. Thus, initially the CB is highly ionized. But, for small values of
.
In quasi equilibrium, the ionization rate per unit
volume, which is proportional to the number density of recombined hydrogen
atoms, must be equal to the recombination rate per unit volume, which is
proportional to the product of the ion and free electron densities in the
CB. Thus, initially the CB is highly ionized. But, for small values of 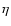 and later times when
and later times when 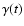 becomes sufficiently small,
equilibrium between the ionization and recombination rates in the partially
ionized hydrogenic plasma results in
becomes sufficiently small,
equilibrium between the ionization and recombination rates in the partially
ionized hydrogenic plasma results in


Up: On the radio afterglow bursts
Copyright ESO 2003
![]() .
.
![]() ,
is given by
,
is given by
![]() ,
with
,
with
![]() cm2 (
cm2 (
![]() cm
is the Bohr radius
and
cm
is the Bohr radius
and ![]() is the Gaunt factor
for photoabsorption by hydrogen).
For the surface flux of photons of Eq. (6), we obtain
an ionization rate of the nth level of atomic hydrogen:
is the Gaunt factor
for photoabsorption by hydrogen).
For the surface flux of photons of Eq. (6), we obtain
an ionization rate of the nth level of atomic hydrogen: