An extensive examination of the variety of error sources due to the
practical and instrumental constraints was done in the preceding
Paper I. The induced aberrations due to defocusing by a shifted
object in the CONICA stand-alone case have been simulated and proven
to be negligible. The influence of the pupil shape and its
numerization have been evaluated, errors taken in account with regard
to the camera pixel scale and the defocus distance deviations have
been simulated and the problem of different object structure was
considered. Furthermore we focused in detail on the handling of data
reduction, e.g. the influence of the different noise sources such as
readout noise or pickup noise. In Paper I we state that all these
error sources accumulate to ![]() nm rms for the focus
coefficient (4). Since the presented calibration data of this paper
are acquired with an optimized Zernike tool, the expected error should
be well below this number. The accuracy of the higher order
coefficients has not changed and amounts to about
nm rms for the focus
coefficient (4). Since the presented calibration data of this paper
are acquired with an optimized Zernike tool, the expected error should
be well below this number. The accuracy of the higher order
coefficients has not changed and amounts to about ![]() nm rms.
nm rms.
In this section we describe how the overall wavefront error can be decomposed and assigned to its corresponding optical components. Then we present the experimental results for one camera objective and some selected filters of CONICA as well as the results for the dichroics of NAOS.
In principal, we have to differentiate between three categories of optical components in the imaging path: the NAOS dichroics, the CONICA filters and the camera objectives.
The contribution of the NAOS dichroics
![]() can be
determined by subtracting the overall NAOS-CONICA instrument aberrations
can be
determined by subtracting the overall NAOS-CONICA instrument aberrations
![]() from the total CONICA instrument aberrations
from the total CONICA instrument aberrations
![]() :
:
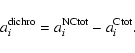 |
(2) |
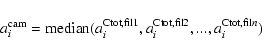 |
(3) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig/f2914_06.ps} \end{figure}](/articles/aa/full/2003/07/aa2914/Timg27.gif) |
Figure 5: CONICA internal aberrations measured by 19 NB filters in K-band with camera objective C50S and pinhole pair 0/4 mm. The thick line indicates the median representing the camera aberrations. The dashed line highlights the aberrant filter NB2.09 which is picked out for the demonstration images in Fig. 6. |
Figure 4 shows the aberrations for all eight narrow band
filters in J- and H-band of CONICA. The camera objective C50S and the
pinhole pair (0/2 mm) is used to obtain the calibration data. The
fourth coefficient
![]() expressing the defocus
shows a peak-to-peak variation of up to 60 nm. This implies a slight
imprecision of coplanarity of the filters in the cold environment.
The other measured coefficients associated with the different filters
noticeably resemble each other. This is evidence that these
narrow-band filters contribute little to the total aberration of the
system and mainly the camera objective aberration is seen.
expressing the defocus
shows a peak-to-peak variation of up to 60 nm. This implies a slight
imprecision of coplanarity of the filters in the cold environment.
The other measured coefficients associated with the different filters
noticeably resemble each other. This is evidence that these
narrow-band filters contribute little to the total aberration of the
system and mainly the camera objective aberration is seen.
Figure 5 displays the calibration results in the K-band. In total, 19 filters have been calibrated using the pinhole pair 0/4 mm. One of the strongly aberrant filters (NB2.09) is highlighted by a dashed line. A large defocus in comparison to the other ones is detected. This filter is expected to have a striking error of coplanarity. It is not surprising that the strong defocus comes along with a particularly high spherical aberration (i=11). The other highly aberrant filters show the same behaviour in comparison with the common filters of minor aberrations. The spherical aberration expresses the next order of a radial symmetric Zernike mode. The probability that a strong default of coplanarity induces only a defocus and does not concern higher orders is small. The PD input images of this aberrant filter is depicted at the bottom of Fig. 6. The right image shows the PSF registered in focus, and the left image a PSF having introduced a defocus of 4 mm. Already the in-focus image reveals a strong degradation, but especially the phase inversion due to the high defocus can be clearly seen in the out of focus image. A bright spot emerges in the center of the "donut''. On the top of this couple of images another couple of images is depicted. These are the PD input data of a filter (NB2.06) with normal behaviour and without strong aberrations.
As described in Sect. 4.2 the median of each Zernike
number of the whole set of vectors yield the vector describing the camera
contribution.
The accuracy of separating the camera aberrations from the raw aberrations (filters including camera) by the method described above is striking. The median aberrations for the filters of the two different wavelength regions plotted in Figs. 4 and 5 are compiled in Table 2. The deviations of both median values are clearly below the expected error (see Sect. 4.1). Table 2 lists these median coefficients taken from all NB filters in J-, H- and K-band. Keeping in mind that the achievable precision is a few nm we state that the camera aberrations are very small. The highest contributions arise from the focus term (4) and the astigmatism (5, 6). Section 5.3 gives an idea of the impact on the image quality dealing with Zernike mode aberrations in this order of magnitude. The residual filter aberrations are obtained by Eq. (4). In general, besides the focus coefficient and a few deviating filters these values are close to zero, too.
| Bands for median | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| J, H | -12 | -34 | 30 | -6 | 4 | 2 | 13 | -8 | 2 | 0 | 9 | -1 |
| K | -15 | -39 | 27 | -10 | 7 | 3 | 15 | -9 | 2 | 0 | 6 | -1 |
| J, H, K | -15 | -39 | 27 | -9 | 6 | 2 | 13 | -9 | 2 | 0 | 7 | -1 |
In the following the properties of the five NAOS dichroics are itemized:
The calibration results are compiled in Table 3 and Table 4. The first table lists the direct PD results. Any correction performed by these coefficients would only apply to the instrument configuration that was used to obtain the calibration data. The second table lists the aberrations directly assigned to the dichroics. These were obtained by subtracting the total CONICA aberrations that have been measured with the same filter and camera objective using the Zernike tool. It is noteworthy that the sensed astigmatism (Zernike number 5, 6) in the separated case is higher than in the overall case. Obviously a part of the camera astigmatism is compensated by the dichroics.
It is noteworthy that this tendency applies for all dichroics. Different reasons can cause this behaviour. First, the inclination of the dichroics artificially introduce an astigmatism. Even if the NAOS dichroics are designed for prism shape and do correct for this effect, a residual error cannot be excluded. Furthermore a certain amount of astigmatism can be introduced by components other than the dichroics lying in the same part of the light path, e.g. the output folding mirror or the CONICA entrance window (see Fig. 1). Nevertheless, it is not a limitation of the calibration method but only a question of assigning the contribution of the wavefront errors to the different optical components. In the end, only the sum of all aberrations has to be correct.
| Dichro | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| VIS | 15 | -5 | 24 | -6 | 23 | 5 | -8 | -9 | 7 | -13 | -7 | 3 |
| N20C80 | 2 | -1 | 42 | -2 | 30 | 5 | -4 | 14 | -1 | -19 | -8 | 4 |
| N90C10 | -7 | -3 | 36 | -3 | 19 | 6 | -5 | -28 | 1 | -9 | -9 | 1 |
| K | -8 | 14 | -17 | -4 | 18 | 3 | -5 | -6 | 7 | -14 | -10 | 2 |
Dichro |
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| VIS | -18 | 37 | -5 | 3 | 16 | 2 | -21 | -44 | 6 | -13 | -14 | 6 |
| N20C80 | -32 | 41 | 13 | 8 | 23 | 1 | -17 | -21 | -3 | -18 | -15 | 6 |
| N90C10 | -41 | 38 | 7 | 7 | 12 | 3 | -18 | -64 | -1 | -9 | -16 | 4 |
| K | -42 | 56 | -47 | 5 | 11 | -1 | -18 | -42 | 5 | -14 | -17 | 5 |
Copyright ESO 2003