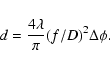3 Phase diversity setup

Our input for phase diversity wavefront estimation are two images: one of them in focus and the other one out of focus. In this manner we introduce the well-known phase diversity which is an obligatory input parameter for PD. One should recall that best phase diversity estimates are to be expected applying a peak to valley phase diversity $\Delta\phi$ between $1 \pi$ and $3 \pi$ and the input images must be at least Nyquist sampled (Paper I). The corresponding defocus distance d depending on the applied wavelength is obtained by

$$d = \frac{4 \lambda}{\pi} (f/D)^2 \Delta\phi.$$ (1)

In the next two subsections we describe in detail two ways of introducing this phase diversity. Both ways are essential to enable us to separate the wavefront error and to assign it to different contributors. This disentanglement is described in Sect. 4.2.

  
3.1 CONICA stand-alone: Focus shift by object

First, we regard the possibilities to obtain the necessary input images with CONICA stand-alone. The CONICA detector is mounted on a tunable stage which is software controlled and can be driven in the cold environment. This allows us in principal to obtain a defocused image but the focus drive spans only a region of 2 mm. Using Eq. (1) we compile for all available camera objectives the necessary defocus distances in the detector plane corresponding to a diversity of $2 \pi$ at a wavelength of 1 $\mu$m in Table 1. Only for the low magnification cameras (C06, C12) is the defocus distance sufficient. But these very cameras undersample in K and at shorter wavelengths so that the focus stage mechanism finally fails in every case. For that reason we swerve to the entrance focal plane. Here a phase diversity of 2 $\pi$corresponds to 1.8 mm at a wavelength of 1 $\mu$m or 3.6 mm at 2 $\mu$m, which is small enough to be implemented in the entrance focal plane. In this plane a wheel is located carrying different field limiting masks, coronographic masks and the slits for spectroscopy. On the wheel we implement four different pinholes at different axial positions. The pinhole diameter is 10 $\mu$m. One pinhole is placed exactly in the entrance focal plane and yields a focused image on the detector (0 mm), and three other pinholes are located 1 mm, 2 mm and 4 mm out of the entrance focal plane. The four pinholes are mounted onto a plate fitting in a socket of the mask wheel. This device will be referred to as a Zernike tool later on. Impacts on the PD estimation due to the mechanical precision of the pinhole positions and possible deviations of their shape are investigated in Paper I.

Figure 2: The Zernike tool with its pinholes in the light path of CONICA.

Figure 2 depicts the setup for the CONICA internal phase diversity measurements. The leftmost component carries the four pinholes, which are shifted against each other, with the values given above. In rotating the wheel holding the Zernike tool we are able to select a pinhole in the field of view. After a collimating lens and a pupil stop, a filter selects the wavelength range and finally the camera objective forms the object image on the detector. The chosen camera objective determines the f-ratio and the pixel scale.

To center the image of the pinholes on the detector, the whole pinhole mount is shifted by turning the mask wheel. In principal PD needs the input images to be on the same spot to ensure that the same aberrations are sensed. The horizontal position of the pinholes can be controlled by adjusting the rotation angle of the wheel. In vertical direction there is no degree of freedom, but the four pinholes are mounted circularly to compensate for the circular movement. By this means a vertical precision of 50 mas (C50S) can be reached. This is easily sufficient not to see any influence due to field aberration effects. PD measurements taken at different detector positions and calculations performed with an optical design software showed that even at the corner of the field of view (13 arcsec) the field aberration is negligible (Paper I). Note that for some measurements in Paper I an earlier version of the Zernike tool was used with a design not optimized for the circular movement of the pinholes. The worst separation that could occur with the former Zernike tool was about 1.3 arcsec. But even with this tool no relevant impact on the precision of wavefront sensing was detected.

Apart from the fact that the Zernike tool with its pinholes at the entrance focal plane provides the required focus shifts, it is convenient that the required focus shifts do not depend on the camera objective (pixel scale) anymore. But note: defocusing by moving an object in the entrance focal plane does not correspond exactly to a defocus due to a shifted detector plane. An investigation of this effect is done in Paper I and turns out to be negligible.

To summarise this section: the PD input data to derive the total CONICA internal aberrations are obtained by object defocusing in the CONICA entrance focal plane. The object defocusing is realized by four 10 $\mu$m pinholes at different axial positions. Note that since the entrance focal plane of CONICA is located inside the cold cryostat, aberrations accrued from the CONICA entrance window are not included in this wavefront estimation.

  
3.2 NAOS-CONICA: Focus shift by the deformable mirror

Now, we describe how the PD input images are obtained which are used to sense the wavefront aberrations of the whole instrument, i.e., the adaptive optics NAOS together with its infrared camera CONICA. In this case we can take advantage of the AO system's capabilities to itself introduce an adequate focus shift and thus there is no need for the implementation of a special tool or a modifaction of the design.

In the entrance focal plane of NAOS, which coincides with the VLT Nasmyth focal plane, a calibration point source can be slid in and imaged by CONICA. This point source is realized by the output of a fiber with a diameter of 10 $\mu$m fixed on a movable stage. On the same stage a second source much larger in diameter (400 $\mu$m) is mounted. It is only seen by the WFS and serves as a reference source to close the loop. This extended source is needed for technical reasons. In the case of no atmospheric turbulence the more extended source provides a much better feed-back signal to the WFS than the small one. By this means the AO control loop is adjusted for any aberrations emerging in the common path. To obtain the focus shift affecting the entire instrument, we introduce the desired amount of defocusing in the WFS path by moving the mirrors of the field selector. During this process the loop is kept closed. Instantly, the arising focus shift is detected by the WFS. Correspondingly, the real time computer commands the DM to compensate for the detected defocus. Finally, the spots on the Shack-Hartmann WFS are centered again, but the defocus of the DM takes effect in the imaging path. For a pure defocus the DM will take a parabolic shape. The maximum achievable defocus by this method is limited by the DM's stroke and turns out to be about 20 mm. Refering to Table 1, this is enough to introduce the needed diversity for an f/15 beam.

The procedure is shown in Fig. 3 and provides us with the PD input data to estimate the NAOS-CONICA overall wavefront errors. In comparison with the procedure described in Sect. 3.1 we deal with the same object now, and we must not care about any deviations in the position of the image pairs. This simplifies data aquisition for the measurement and diminishes the number of possible error sources.

Figure 3: Defocusing in closed loop using the NAOS Field Selector