

Up: Calibration of NAOS and
Subsections
5
Image quality versus estimated aberrations
The PD calibration data can be used to investigate the available image
quality in different ways. First, the knowledge of the wavefront
allows us to calculate a SR. After the reduction of the calibration data
the wavefront is described by a set of Zernike coefficients.
Furthermore, we can just refer to the in-focus image and calculate a
SR with the measured point spread function. In the following we give a
more detailed explanation of how these SRs are obtained.
For small wavefront deviations the SR can be determined via the
coherent energy referring to the wavefront variance 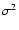 in
radian. The PD estimation yield the wavefront expanded in terms of
Zernike coefficients ai. For small
in
radian. The PD estimation yield the wavefront expanded in terms of
Zernike coefficients ai. For small 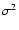
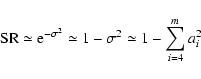 |
(5) |
allows us to calculate the SR directly by the output of PD estimation. In
principal the sum runs to infinity (
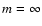 )
but for our purpuse
we stop at m = 15. We can compare these SR numbers to the ones that
are directly determined by the in-focus images.
)
but for our purpuse
we stop at m = 15. We can compare these SR numbers to the ones that
are directly determined by the in-focus images.
A straight-forward way to calculate a SR on the focus image (PSF) is
to construct a theoretical diffraction-limited image
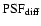 taking into account the wavelength, the pixel
scale, the aperture and the central obscuration
taking into account the wavelength, the pixel
scale, the aperture and the central obscuration![[*]](/icons/foot_motif.gif) . Having normalized the total intensity of the PSF and
. Having normalized the total intensity of the PSF and
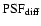 to 1, the fraction of these values yields the SR
(see Eq. (6)).
to 1, the fraction of these values yields the SR
(see Eq. (6)).
In particular, in the case of the PSF sampling being close to the
Nyquist criterion this approach has the disadvantage of being sensitive
to the exact position of the PSF peak with respect to the pixel
center. Furthermore, since the total intensity has to be determined by
the integrated signal over a wider region around the PSF, the
reliability of the SR value depends on a precise background
correction. If the background is overestimated, then the SR will be
overestimated, too, and vice versa. The reliability of the SR values
can be enhanced when we switch from the image space to the Fourier
space by
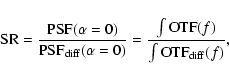 |
(6) |
where OTF is the optical transfer function.
Since in Fourier space only spatial frequencies are considered, a shift of the
PSF is of no importance anymore. Aside from that, an elegant and reliable
background correction can be performed using the zero spatial frequency. We
calculate the SRs by the following procedure![[*]](/icons/foot_motif.gif) :
:
- The image is corrected by its corresponding background;
- The OTF is calculated. It is given
by the real part of the Fourier transform of the image;
- The residual background is corrected by the zero frequency. A
fit of the very first spatial frequencies is used to extrapolate the true zero
frequency value. The difference of the measured and the extrapolated value for
the zero frequency yields the residual background;
- The noise level is subtracted using the high frequencies beyond the
diffraction limit;
- A theoretical telescope OTF is constructed and multiplied by a Bessel
function to account for the spatial spread due to the object size;
- The detector response is taken into account. This is done by a further
multiplication of the theoretical telescope OTF with the Fourier transform of
the detector response;
- The SR is obtained by the division of the normalized integrals
from the measured and the theoretical OTF. All points with spatial frequencies
higher than the diffraction limit are excluded.
Figure 7 gives an example of how the described OTFs look
for a PSF taken through the filter H2(1_0)S(7). To allow for a one
dimensional representation, the circular mean of the two dimensional
OTF is calculated. The raw, untreated OTF of the image is labeled
"OTF image''. "OTF corr'' displays the image OTF which is corrected
for the residual background at zero frequency and for the noise
level. The noise level of the uncorrected image OTF can be seen as
plateau beyond the cutoff frequency  and averages 1% of
the maximum value. The theoretical diffraction-limited telescope OTF
includes the reduction due to the object size
and averages 1% of
the maximum value. The theoretical diffraction-limited telescope OTF
includes the reduction due to the object size![[*]](/icons/foot_motif.gif) and the correction for the detector modulation transfer
function (MTF). It is labeled "MTF Det'' and is located at the top of
the plot. The detector response is constructed by the assumption that
roughly 3% of the total intensity is contained at each of the
adjacent pixels and 1.5% in the corner pixels. Here we refer to Finger et al. (2000).
In this paper a measurement of the response of a
comparable infrared array is described. Due to the lack of a precise
knowledge of the detector response it is constructed by a quadratic
scaling in relation to the different pixel size
and the correction for the detector modulation transfer
function (MTF). It is labeled "MTF Det'' and is located at the top of
the plot. The detector response is constructed by the assumption that
roughly 3% of the total intensity is contained at each of the
adjacent pixels and 1.5% in the corner pixels. Here we refer to Finger et al. (2000).
In this paper a measurement of the response of a
comparable infrared array is described. Due to the lack of a precise
knowledge of the detector response it is constructed by a quadratic
scaling in relation to the different pixel size![[*]](/icons/foot_motif.gif) . A
quadratic scaling is implied by a linear behaviour of the diffusion
of the minority carriers in the detector material in one dimension
for small distance variations.
. A
quadratic scaling is implied by a linear behaviour of the diffusion
of the minority carriers in the detector material in one dimension
for small distance variations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig/f2914_11.ps} \end{figure}](/articles/aa/full/2003/07/aa2914/Timg38.gif) |
Figure 7:
Visualization of the theoretical and measured OTF at the
example of filter FeII1644.
|
5.2
Comparison of Strehl ratios
The resulting SRs for the narrow-band filters in J, H, and K are
presented in Figs. 8 and 9.
For each filter two SRs are given: the SR by PD and the SR on the
image.
A number of error sources contribute to the error of the SR values on
image. Beside of small error contributions due to uncertainties of
the pixel scale and the flatfield, the remaining uncertainty of the
background correction and the detector response lead us to estimate an
absolute error of 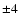 %. The expected wavelength dependency of
the MTF error is minor with respect to the remaining background
error. Therefore it is neglected and we use the constant value given
above derived from experience in reducing the experimental data.
%. The expected wavelength dependency of
the MTF error is minor with respect to the remaining background
error. Therefore it is neglected and we use the constant value given
above derived from experience in reducing the experimental data.
Recall that the SR by PD has a maximal wavelength-dependent
error of 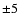 % at 1
% at 1 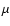 m and
m and 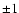 % at 2
% at 2 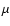 m taking
into account an error of
m taking
into account an error of 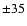 nm RMS for the focus estimation
(i=4). The main contributor to this error is a systematic error in
the precision of the pinhole positions in the Zernike tool (see
Sect. 4.1).
nm RMS for the focus estimation
(i=4). The main contributor to this error is a systematic error in
the precision of the pinhole positions in the Zernike tool (see
Sect. 4.1).
In general the PD SRs exceed the other SR values. This reflects the
fact that the wavefront is expanded by a limited number of Zernike
coefficients and the higher order aberrations are cut off. Note that
it is not astonishing that in the case of very low SR values (worse than
50%) the PD SR value may lie below the image SRs
(Fig. 9). Such strong wavefront errors violate the
condition under which Eq. (5) is valid. Thus, we expect
Eq. (5) to yield underestimated values.
The comparison of the SR values determined by the different methods
turns out to be consistent. The longer the wavelength, the more the
image and PD SR values approach each other. This shows that the
influence of aberrations scales with the wavelength. In other words,
the fact that we cut off at a certain Zernike number (i=15) has a
greater impact at short wavelengths.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig/f2914_12.ps} \end{figure}](/articles/aa/full/2003/07/aa2914/Timg41.gif) |
Figure 8:
Comparison of SR versus wavelength in J and H band calculated directly
and derived from PD results. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig/f2914_13.ps} \end{figure}](/articles/aa/full/2003/07/aa2914/Timg42.gif) |
Figure 9:
Comparison of SR versus wavelength in K band calculated directly and
derived from PD results. |
5.3 Focus adjustment
Having in mind the small estimated wavefront errors that we presented in the
previous sections we become conscious of the required precision of the most
trivial aberration we regard: the focus. It is striking that even in the
focus determination we depend on the precision of PD calibration. This becomes
evident when we look at the conventional procedure of focus tuning and regard
the loss of SR caused by the detected aberrations.
To tune the focus of CONICA, the in-focus pinhole of the Zernike tool
is imaged on the detector. Now, a focus curve is obtained by taking
images at different axial position of the detector stage (see Sect. 3.1). The maximum of the SRs indicate
the proper focus position of the stage. The maximum of the obtained
focus curves for the different cameras can be located with an accuracy
of about 50 nm rms. For this wavefront error, Eq. (5)
yields a loss of SR of 2.5% at a wavelength of 2 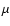 m and almost
10% at 1
m and almost
10% at 1 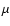 m. Thus, in particular in the J- and H-band, the
inaccuracy of determining the focus only by moving the detector stage
gives reason for a significant loss of SR. Furthermore the whole
effort of fine-tuning for the remaining static wavefront aberrations
becomes irrelevant when the remaining focus error is in the regime of
the highest higher-level aberrations (Zernike number
m. Thus, in particular in the J- and H-band, the
inaccuracy of determining the focus only by moving the detector stage
gives reason for a significant loss of SR. Furthermore the whole
effort of fine-tuning for the remaining static wavefront aberrations
becomes irrelevant when the remaining focus error is in the regime of
the highest higher-level aberrations (Zernike number 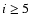 ). Compare the aberrations for focus with astigmatism in
Figs. 4 and 5. The only way to achieve a
significant improvement of the wavefront error, and therefore of the
SR after closed loop compensation, is to ensure that the
residual focus deviation is corrected properly, too. This is
guaranteed by following the procedure:
). Compare the aberrations for focus with astigmatism in
Figs. 4 and 5. The only way to achieve a
significant improvement of the wavefront error, and therefore of the
SR after closed loop compensation, is to ensure that the
residual focus deviation is corrected properly, too. This is
guaranteed by following the procedure:
- Determination of the rough nominal focus position of the CONICA
detector for each camera with one reference filter. The in-focus pinhole of
the Zernike tool serves as a reference;
- Determination of the nominal focus for the whole
instrument. The calibration point source in the NAOS entrance focal
plane serves as a reference. The data points for the focus curve are
obtained by moving the field selector in closed loop. This has to
be done for every NAOS dichroic;
- The corresponding data base entries are updated by the nominal
focus positions (CONICA internal and NAOS). The nominal focus
deviations are included in the data base. They are compensated for by moving
the field selector in the case of switching the NAOS dichroics and by
moving the CONICA detector stage in the case of switching the camera
objectives;
- Then the PD estimation reveals the residual focus error for
each configuration, in particular for each filter. They are entered
into the data base together with the higher order aberrations. For a
certain instrument configuration the corresponding values are
fetched automatically and delivered to the AO system. The DM corrects
for the residual focus deviations.


Up: Calibration of NAOS and
Copyright ESO 2003
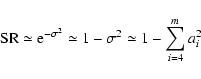
![]() %. The expected wavelength dependency of
the MTF error is minor with respect to the remaining background
error. Therefore it is neglected and we use the constant value given
above derived from experience in reducing the experimental data.
%. The expected wavelength dependency of
the MTF error is minor with respect to the remaining background
error. Therefore it is neglected and we use the constant value given
above derived from experience in reducing the experimental data.
![]() % at 1
% at 1 ![]() m and
m and ![]() % at 2
% at 2 ![]() m taking
into account an error of
m taking
into account an error of ![]() nm RMS for the focus estimation
(i=4). The main contributor to this error is a systematic error in
the precision of the pinhole positions in the Zernike tool (see
Sect. 4.1).
nm RMS for the focus estimation
(i=4). The main contributor to this error is a systematic error in
the precision of the pinhole positions in the Zernike tool (see
Sect. 4.1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig/f2914_12.ps} \end{figure}](/articles/aa/full/2003/07/aa2914/Timg41.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig/f2914_13.ps} \end{figure}](/articles/aa/full/2003/07/aa2914/Timg42.gif)
![]() m and almost
10% at 1
m and almost
10% at 1 ![]() m. Thus, in particular in the J- and H-band, the
inaccuracy of determining the focus only by moving the detector stage
gives reason for a significant loss of SR. Furthermore the whole
effort of fine-tuning for the remaining static wavefront aberrations
becomes irrelevant when the remaining focus error is in the regime of
the highest higher-level aberrations (Zernike number
m. Thus, in particular in the J- and H-band, the
inaccuracy of determining the focus only by moving the detector stage
gives reason for a significant loss of SR. Furthermore the whole
effort of fine-tuning for the remaining static wavefront aberrations
becomes irrelevant when the remaining focus error is in the regime of
the highest higher-level aberrations (Zernike number ![]() ). Compare the aberrations for focus with astigmatism in
Figs. 4 and 5. The only way to achieve a
significant improvement of the wavefront error, and therefore of the
SR after closed loop compensation, is to ensure that the
residual focus deviation is corrected properly, too. This is
guaranteed by following the procedure:
). Compare the aberrations for focus with astigmatism in
Figs. 4 and 5. The only way to achieve a
significant improvement of the wavefront error, and therefore of the
SR after closed loop compensation, is to ensure that the
residual focus deviation is corrected properly, too. This is
guaranteed by following the procedure: