

Up: Particle acceleration in rotating
Subsections
In order to gain insight into the particle transport and acceleration
process, let us first consider the influence of rigid rotation profiles.
One may associate such rotation profiles with dynamo action in the inner
accretion disk around a spinning black hole, which creates a jet
magnetosphere filled with disk plasma and rotating with the angular
frequency of its foot points concentrated near the innermost stable
orbit (e.g. Camenzind 1996).
The acceleration of particles due to rigid rotation could represent an
efficient process for the production of high energy particles.
This was demonstrated by Rieger & Mannheim (2000)
for the centrifugal acceleration of charged test particles at the
base of a rigidly rotating jet magnetosphere for conditions assumed to
prevail in AGN-type objects.
In such cases an upper limit for the maximal attainable Lorentz factor can
be established, which is given by the breakdown of the bead-on-the-wire
approximation in the vicinity of the light cylinder.
There are several similarities to the application presented here:
If we consider the transport of relativistic particles in a rigidly
rotating background flow (i.e.
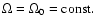 )
by utilising
the above model, shearing is absent (i.e.
)
by utilising
the above model, shearing is absent (i.e.
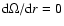 )
and
thus particle energization only occurs as a consequence of the
interaction with the accelerating background flow, i.e. due to the presence
of centrifugal effects.
It can then be readily shown that for the case considered here,
Eq. (4) is analogous to the Hamiltonian for a bead on a rigidly
rotating wire (cf. Webb et al. 1994, also Rieger & Mannheim
2001a), i.e.
)
and
thus particle energization only occurs as a consequence of the
interaction with the accelerating background flow, i.e. due to the presence
of centrifugal effects.
It can then be readily shown that for the case considered here,
Eq. (4) is analogous to the Hamiltonian for a bead on a rigidly
rotating wire (cf. Webb et al. 1994, also Rieger & Mannheim
2001a), i.e.
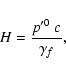 |
(8) |
while the transport equation becomes purely spatial.
The variable H introduced above, could thus be regarded as describing the
balance between the centrifugal force and the inertia of the particle in
the comoving frame.
By means of Noether's theorem, H could be shown to be a constant of
motion, and hence Eq. (C.12) indicates that the ratio of
particle to flow Lorentz factor is fixed. The comoving particle momentum
p' can then be simply expressed as a function of the
radial coordinate r, i.e.
p' = p'(r) (cf. Fig. 1).
We may easily solve the resultant (spatial) transport equation analytically,
assuming homogeneous boundary conditions at the jet inner radius
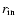 and its relevant outer radius
and its relevant outer radius
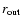 .
In the present
case, one may choose the size of the inner radius
.
In the present
case, one may choose the size of the inner radius
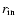 to be of the
order of the radius of the innermost stable orbit around a rotating black
hole, while the outer radius
to be of the
order of the radius of the innermost stable orbit around a rotating black
hole, while the outer radius
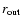 is at any rate physically
constrained to be smaller than the light cylinder radius (note that for
relativistic MHD winds, the Alfvén point may be close to the
light cylinder).
Results concerning the particle transport are presented in Figs. 1
and 2.
They indicate that the energetic particles injected at
is at any rate physically
constrained to be smaller than the light cylinder radius (note that for
relativistic MHD winds, the Alfvén point may be close to the
light cylinder).
Results concerning the particle transport are presented in Figs. 1
and 2.
They indicate that the energetic particles injected at 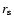 will gain
energy by being transported in the rigidly rotating background flow,
i.e. due to the impact of centrifugal acceleration the particle momentum
increases with position as expected. The precise evolution in the
immediate vicinity of the light cylinder should however be treated with
some caution due to the limitations imposed by the applied diffusion
approach.
Figure 2 reveals a decrease in efficiency if the time
will gain
energy by being transported in the rigidly rotating background flow,
i.e. due to the impact of centrifugal acceleration the particle momentum
increases with position as expected. The precise evolution in the
immediate vicinity of the light cylinder should however be treated with
some caution due to the limitations imposed by the applied diffusion
approach.
Figure 2 reveals a decrease in efficiency if the time
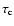 between two collisions increases with momentum (in case of a very weak
spatial dependence), i.e. if scattering occurs less rapidly for the higher
than for the lower energy particles.
between two collisions increases with momentum (in case of a very weak
spatial dependence), i.e. if scattering occurs less rapidly for the higher
than for the lower energy particles.
![\begin{figure}
\par\includegraphics[width=9.2cm]{MS2486f1.eps} \end{figure}](/articles/aa/full/2002/48/aa2486/Timg53.gif) |
Figure 1:
Particle momentum p' as a function of the radial coordinate
in the case of rigid rotation, for particles injected at
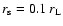 with initial Lorentz factor
with initial Lorentz factor
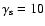 (solid) and 15
(dashed). Here,
(solid) and 15
(dashed). Here, 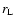 is defined by
is defined by
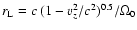 |
Let us now consider the acceleration of particles due to a rotating
background flow with keplerian rotation profile
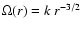 ,
where
,
where
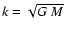 .
Again, such flow profiles might be associated with jets or disk winds
originating from the accretion disk around the black hole and dragging
the Keplerian disk rotation with them. Hence, for reasons of
self-similarity, keplerian rotation may be intuitively regarded as one
of the most characteristical descriptions with respect to the velocity
profile of intrinsically rotating flows.
For example, Lery & Frank (2000) recently investigated
the structure and stability of astrophysical jets including Keplerian
rotation in the outermost part of the outflow and rigid rotation close
to its axis (cf. also Hanasz et al. 2000).
They also studied the application to non-relativistic outflows from
young stellar objects. One may thus eventually consider a simple model
where particles, accelerated in a rigidly rotating flow, are subsequently
injected into a Keplerian rotating flow.
Generally, if we consider Keplerian rotation, both shear and centrifugal
effects are present. For non-relativistic rotation, analytical solutions
of the Fourier transformed transport equation are given in the
Appendix C.2. in terms of the confluent hypergeometrical functions.
Such solutions should be appropriate for the outer jet regions. As the
relative strength of the contribution by shear to that of centrifugal
energization evolves with r, shear effects will eventually dominate
over centrifugal acceleration (see discussion).
This is particularly illustrated in Fig. 3, where we
have plotted the logarithm of the (normalized) particle distribution
function f above
.
Again, such flow profiles might be associated with jets or disk winds
originating from the accretion disk around the black hole and dragging
the Keplerian disk rotation with them. Hence, for reasons of
self-similarity, keplerian rotation may be intuitively regarded as one
of the most characteristical descriptions with respect to the velocity
profile of intrinsically rotating flows.
For example, Lery & Frank (2000) recently investigated
the structure and stability of astrophysical jets including Keplerian
rotation in the outermost part of the outflow and rigid rotation close
to its axis (cf. also Hanasz et al. 2000).
They also studied the application to non-relativistic outflows from
young stellar objects. One may thus eventually consider a simple model
where particles, accelerated in a rigidly rotating flow, are subsequently
injected into a Keplerian rotating flow.
Generally, if we consider Keplerian rotation, both shear and centrifugal
effects are present. For non-relativistic rotation, analytical solutions
of the Fourier transformed transport equation are given in the
Appendix C.2. in terms of the confluent hypergeometrical functions.
Such solutions should be appropriate for the outer jet regions. As the
relative strength of the contribution by shear to that of centrifugal
energization evolves with r, shear effects will eventually dominate
over centrifugal acceleration (see discussion).
This is particularly illustrated in Fig. 3, where we
have plotted the logarithm of the (normalized) particle distribution
function f above
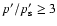 for
for 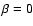 (i.e. allowing no
spatial dependence of the diffusion coefficient) and different
momentum dependence of
(i.e. allowing no
spatial dependence of the diffusion coefficient) and different
momentum dependence of 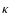 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS2486f2.eps} \end{figure}](/articles/aa/full/2002/48/aa2486/Timg60.gif) |
Figure 2:
Spatial distribution
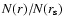 for rigid rotation
using a different energy dependence of the diffusion coefficients, i.e.
for rigid rotation
using a different energy dependence of the diffusion coefficients, i.e.
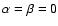 (solid line),
(solid line), 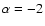 , ,
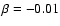 (dotted line)
and
(dotted line)
and 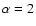 , ,
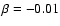 (dashed line). Boundary conditions
(dashed line). Boundary conditions
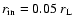 , ,
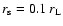 and
and
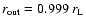 have been used for the
calculations.
have been used for the
calculations. |
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS2486f3.eps} \end{figure}](/articles/aa/full/2002/48/aa2486/Timg66.gif) |
Figure 3:
The momentum-dependence of the (normalized) distribution
function f for Keplerian rotation using 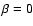 ,
calculated for ,
calculated for
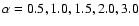 at fixed
at fixed
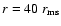 .
Boundary and injection conditions have been specified as .
Boundary and injection conditions have been specified as
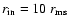 , ,
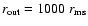 , ,
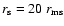 ,
where ,
where
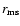 is given by
is given by
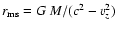 . . |
Most interestingly, well-developed power law momentum spectra are
recovered, which suggest a spectral slope linearly related to
the momentum index of the diffusion coefficient, so that we have
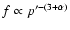 .
This excellently confirms the results
previously derived by Berezhko & Krymskii (1981).
For a collisionless plasma with a simple shear flow
.
This excellently confirms the results
previously derived by Berezhko & Krymskii (1981).
For a collisionless plasma with a simple shear flow
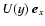 ,
and by using a simple BGK term, they found the shear acceleration to
give rise to a power-law momentum spectrum for the steady state
comoving particle distribution
,
and by using a simple BGK term, they found the shear acceleration to
give rise to a power-law momentum spectrum for the steady state
comoving particle distribution
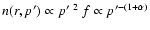 ,
if the collision time
,
if the collision time 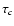 depends on
momentum as
depends on
momentum as
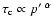 and
and 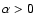 .
However, if the momentum index
.
However, if the momentum index 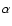 is smaller than zero, i.e.
is smaller than zero, i.e.
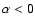 ,
an exponential spectrum may developed.
,
an exponential spectrum may developed.
In the case of flat rotation (i.e.
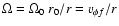 )
one may easily investigate a more complex interplay between shear and
centrifugal effects. For in this case, the relative strength of shear
to centrifugal effects is independent of the radial coordinate and the
general solution of the fourier-transformed equation could be cast in
simple analytical terms allowing basic inverse Fourier integration
to be done, using homogeneous boundary conditions at
)
one may easily investigate a more complex interplay between shear and
centrifugal effects. For in this case, the relative strength of shear
to centrifugal effects is independent of the radial coordinate and the
general solution of the fourier-transformed equation could be cast in
simple analytical terms allowing basic inverse Fourier integration
to be done, using homogeneous boundary conditions at
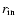 and
and
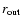 .
For the present application, we have considered typical jet flows
with relativistic
vz/c=0.95 and different azimuthal velocities
.
For the present application, we have considered typical jet flows
with relativistic
vz/c=0.95 and different azimuthal velocities
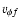 (i.e. for a range of
(i.e. for a range of
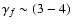 ). The
corresponding results are plotted in Fig. 4
using a constant diffusion coefficient (i.e.
). The
corresponding results are plotted in Fig. 4
using a constant diffusion coefficient (i.e.
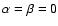 ).
Again, the calculated distribution functions reveal a powerlaw-type
momentum dependence, where for low azimuthal velocities very steep
momentum spectra are recovered, i.e. the momentum exponents are found to
be near by -8.8 (for
).
Again, the calculated distribution functions reveal a powerlaw-type
momentum dependence, where for low azimuthal velocities very steep
momentum spectra are recovered, i.e. the momentum exponents are found to
be near by -8.8 (for
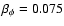 ), -6.9 (for
), -6.9 (for
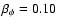 ), -5.1 (for
), -5.1 (for
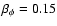 )
and -4.4 (for
)
and -4.4 (for
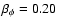 ).
The observed flattening of the spectra with increasing azimuthal
velocities is indicative of the increasing impact of centrifugal
effects.
).
The observed flattening of the spectra with increasing azimuthal
velocities is indicative of the increasing impact of centrifugal
effects.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS2486f4.eps} \end{figure}](/articles/aa/full/2002/48/aa2486/Timg82.gif) |
Figure 4:
The momentum-dependence of the (normalized) distribution
function f(r,p') for flat rotation, calculated for
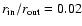 , ,
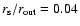 at position
at position
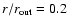 .
Chosen azimuthal velocities are .
Chosen azimuthal velocities are
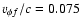 (short-dashed), 0.10 (dotted),0.15 (solid),
0.20 (long-dashed).
(short-dashed), 0.10 (dotted),0.15 (solid),
0.20 (long-dashed). |


Up: Particle acceleration in rotating
Copyright ESO 2002
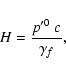
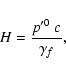
![\begin{figure}
\par\includegraphics[width=9.2cm]{MS2486f1.eps} \end{figure}](/articles/aa/full/2002/48/aa2486/Timg53.gif)
![]() )
one may easily investigate a more complex interplay between shear and
centrifugal effects. For in this case, the relative strength of shear
to centrifugal effects is independent of the radial coordinate and the
general solution of the fourier-transformed equation could be cast in
simple analytical terms allowing basic inverse Fourier integration
to be done, using homogeneous boundary conditions at
)
one may easily investigate a more complex interplay between shear and
centrifugal effects. For in this case, the relative strength of shear
to centrifugal effects is independent of the radial coordinate and the
general solution of the fourier-transformed equation could be cast in
simple analytical terms allowing basic inverse Fourier integration
to be done, using homogeneous boundary conditions at
![]() and
and
![]() .
For the present application, we have considered typical jet flows
with relativistic
vz/c=0.95 and different azimuthal velocities
.
For the present application, we have considered typical jet flows
with relativistic
vz/c=0.95 and different azimuthal velocities
![]() (i.e. for a range of
(i.e. for a range of
![]() ). The
corresponding results are plotted in Fig. 4
using a constant diffusion coefficient (i.e.
). The
corresponding results are plotted in Fig. 4
using a constant diffusion coefficient (i.e.
![]() ).
Again, the calculated distribution functions reveal a powerlaw-type
momentum dependence, where for low azimuthal velocities very steep
momentum spectra are recovered, i.e. the momentum exponents are found to
be near by -8.8 (for
).
Again, the calculated distribution functions reveal a powerlaw-type
momentum dependence, where for low azimuthal velocities very steep
momentum spectra are recovered, i.e. the momentum exponents are found to
be near by -8.8 (for
![]() ), -6.9 (for
), -6.9 (for
![]() ), -5.1 (for
), -5.1 (for
![]() )
and -4.4 (for
)
and -4.4 (for
![]() ).
The observed flattening of the spectra with increasing azimuthal
velocities is indicative of the increasing impact of centrifugal
effects.
).
The observed flattening of the spectra with increasing azimuthal
velocities is indicative of the increasing impact of centrifugal
effects.