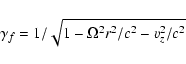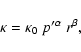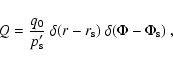Up: Particle acceleration in rotating
By starting from the relativistic Boltzmann equation and by using both
the differential moment equations and a simple BKG (Bhatnagar, Gross &
Krook) time relaxation for the scattering term, the relativistic particle
transport equation in the diffusion approximation was derived by
Webb (1989, 1992; cf. also Appendix A).
In the underlying physical picture, it is assumed that scattering of high
energy particles occurs by small-scale magnetic field irregularities
carried in a collisionless, systematically moving background flow. In each
scattering event the particle momentum is randomized in direction,
but its magnitude p' is assumed to be conserved in the (local) comoving
flow frame, where the electric field vanishes.
Since the rest frame of the scattering centres is regarded to be
essentially that of the background flow, particles neither gain energy
nor momentum merely by virtue of the scattering if there is no shear or
rotation present and the flow is not diverging.
However, in the case of a shear in the background flow, the
particle momentum relative to the flow changes for a particle
travelling across the shear.
As the particle momentum in the local flow frame is preserved in the
subsequent scattering event, a net increase in particle momentum may occur
(cf. Jokipii & Morfill 1990).
Thus, if rotation and shear is present, high energy particles, which do
not corotate with the flow, will sample the shear flow and may be
accelerated by the centrifugal and shear effects (cf. Webb et al. 1994).
For the present application, we consider a rather idealized (hollow)
cylindrical jet model where the plasma moves along the z-axis at
constant (relativistic) vz, while its velocity component in the plane
perpendicular to the jet axis is purely azimuthal and characterized by the
angular frequency 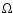 .
Using cylindrical coordinates for the position
four vector, i.e.
.
Using cylindrical coordinates for the position
four vector, i.e.
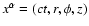 ,
the metric tensor becomes
coordinate-dependent (i.e.
,
the metric tensor becomes
coordinate-dependent (i.e.
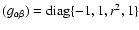 )
and
for the chosen holonomic basis the considered flow four velocity may be
written in shortened notation as
)
and
for the chosen holonomic basis the considered flow four velocity may be
written in shortened notation as
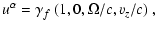 |
|
|
(1) |
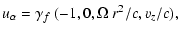 |
|
|
(2) |
where the normalization
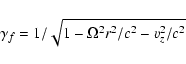 |
(3) |
denotes the Lorentz factor of the flow and where the angular frequency
may be a function of the radial coordinate, i.e.
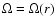 .
As suggested by Webb et al. (1994), the resulting transport
equation may be cast in a more suitable form if one replaces the comoving
variable p' by the variable
.
As suggested by Webb et al. (1994), the resulting transport
equation may be cast in a more suitable form if one replaces the comoving
variable p' by the variable
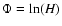 ,
where H is given by
,
where H is given by
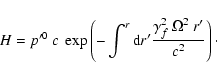 |
(4) |
In the case of highly relativistic particles (with
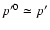 )
and using an (isotropic) diffusion coefficient of the form
)
and using an (isotropic) diffusion coefficient of the form
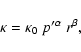 |
(5) |
we finally arrive at the steady state transport equation
(cf. Appendix B) for the (isotropic) phase space
distribution function f(r,z,p')
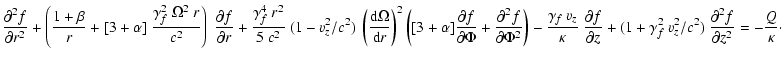 |
|
|
(6) |
In general, the solution of Eq. (6) can be quite
complicated. However, as we are especially interested in the azimuthal
effects of particle acceleration in a rotating flow further along the
jet axis, it seems sufficient for a first approach to search for a
z-independent solution of the transport equation, i.e. we may be
content with an investigation of the one-dimensional Green's function,
which preserves much of the physics involved and which corresponds to
the assumption of a continuous injection along the jet (cf. Appendix C).
In this case the corresponding source term becomes
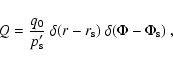 |
(7) |
describing mono-energetic injection of particles with momentum
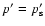 from a cylindrical surface at
from a cylindrical surface at
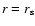 .
Here,
.
Here, 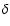 denotes
the Dirac delta distribution and the constant q0 is defined as
denotes
the Dirac delta distribution and the constant q0 is defined as
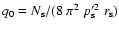 with the total number
with the total number 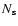 of injected particles. In order to solve the z-independent transport
equation, we then apply Fourier techniques and consider the Green's
solutions satisfying homogeneous, i.e. zero Dirichlet boundary conditions.
of injected particles. In order to solve the z-independent transport
equation, we then apply Fourier techniques and consider the Green's
solutions satisfying homogeneous, i.e. zero Dirichlet boundary conditions.


Up: Particle acceleration in rotating
Copyright ESO 2002
![]() .
Using cylindrical coordinates for the position
four vector, i.e.
.
Using cylindrical coordinates for the position
four vector, i.e.
![]() ,
the metric tensor becomes
coordinate-dependent (i.e.
,
the metric tensor becomes
coordinate-dependent (i.e.
![]() )
and
for the chosen holonomic basis the considered flow four velocity may be
written in shortened notation as
)
and
for the chosen holonomic basis the considered flow four velocity may be
written in shortened notation as