

Up: Particle acceleration in rotating
Appendix B: Derivation of the steady state diffusive particle
transport equation in cylindrical coordinates
Consider for the present purpose a cylindrical jet model where the
plasma moves along the z-axis at constant (relativistic) vz
while the perpendicular velocity component is purely azimuthal, i.e.
characterized by the angular frequency 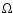 ,
in which case it
proves useful to apply cylindrical coordinates
,
in which case it
proves useful to apply cylindrical coordinates
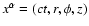 .
One may then choose a set of (non-normalized)
holonomic basis vectors
.
One may then choose a set of (non-normalized)
holonomic basis vectors
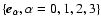 with
with
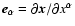 ,
which determine a
1-form basis
,
which determine a
1-form basis
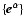 ,
known as its dual basis.
For cylindrical coordinates
,
known as its dual basis.
For cylindrical coordinates
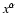 the metric tensor
the metric tensor
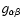 becomes coordinate-dependent, i.e. for the
covariant metric tensor we have
becomes coordinate-dependent, i.e. for the
covariant metric tensor we have
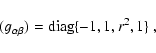 |
(B.1) |
while for the contravariant counterpart is consequently given by
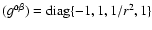 .
In particular, all partial
derivatives of the metric coefficients vanish, except for the
g22 coefficient, and therefore all connection coefficients or
Christoffel symbols of second order vanish, except for
.
In particular, all partial
derivatives of the metric coefficients vanish, except for the
g22 coefficient, and therefore all connection coefficients or
Christoffel symbols of second order vanish, except for
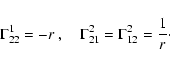 |
(B.2) |
Using the chosen holonomic basis we consider a simple plasma flow
where the four velocity could be written in coordinate form as
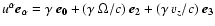 and
and
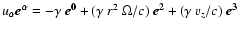 ,
respectively, or in shortened notation as
,
respectively, or in shortened notation as
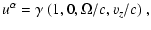 |
|
|
(B.3) |
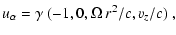 |
|
|
(B.4) |
where the normalization
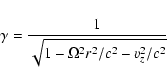 |
(B.5) |
denotes the Lorentz factor of the flow and where the angular
frequency may be selected to be a function of the radial coordinate,
i.e.
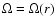 .
.
Generally, for a contravariant four vector
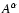 the covariant
derivative is given by
the covariant
derivative is given by
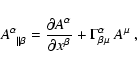 |
(B.6) |
while for the covariant derivative of a covariant four vector
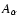 one has
one has
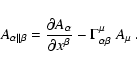 |
(B.7) |
Hence, for the assumed four velocity Eq. (B.3), the
fluid four divergence becomes zero, i.e.
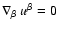 ,
while the fluid four acceleration Eq. (A.4) reduces to
,
while the fluid four acceleration Eq. (A.4) reduces to
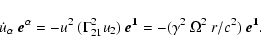 |
(B.8) |
For the components of the shear tensor Eq. (A.6) we may
then derive the following relations
The viscous energization coefficient
Eq. (A.5) then becomes
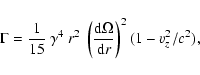 |
(B.10) |
noting that
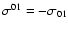 ,
,
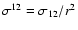 and
and
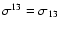 .
.
As the fluid four divergence vanishes, the first term in brackets
of Eq. (A.1) becomes zero, while for the second term in
brackets one finds
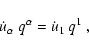 |
(B.11) |
with the radial particle current
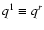 (cf. Eq. (A.3))
(cf. Eq. (A.3))
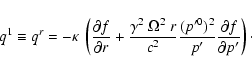 |
(B.12) |
In the steady-state the fifth term in brackets of Eq. (A.1)
becomes
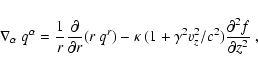 |
(B.13) |
noting that the third component of the heat flux is given by
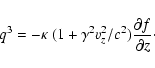 |
(B.14) |
Finally, for the fourth term in brackets of Eq. (A.1) we
have
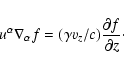 |
(B.15) |
Now, by collecting together all the relevant terms of
Eq. (A.1) and by introducing a source term Q (which may
depend on r, z and p'), we finally arrive at the relevant
relativistic steady-state transport equation in cylindrical coordinates
being appropriate for the considered rotating and shearing jet
flows:
For purely azimuthal, special relativistic flows with vz=0, the
transport Eq. (B.16) reduces to Eq. (5.2)
derived in WJM 94.
As suggested by WJM 94, the derived transport equation may be cast
in a more suitable form by introducing the variable
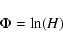 |
(B.17) |
replacing the comoving particle momentum variable p'.
Following WJM 94, we may define H such that
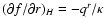 ,
with qr given by Eq. (B.12), the index
H denoting a derivative at constant H, i.e.
,
with qr given by Eq. (B.12), the index
H denoting a derivative at constant H, i.e.
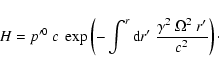 |
(B.18) |
With respect to a physical interpretation of H we would like to note,
that in the case of rigid rotation (i.e.
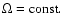 )
H could be
related to the Hamiltonian for a bead on a rigidly rotating wire
(cf. WJM 94; see also Eq. (C.12)).
Hence, by writing
)
H could be
related to the Hamiltonian for a bead on a rigidly rotating wire
(cf. WJM 94; see also Eq. (C.12)).
Hence, by writing
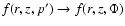 ,
the
relevant derivatives transform like
,
the
relevant derivatives transform like
using
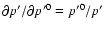 and noting that
and noting that
![$p'^0~c=\exp[\int \mbox{d}r'~\gamma^2~\Omega^2~r'/c^2]~\exp\Phi$](/articles/aa/full/2002/48/aa2486/img169.gif) .
As usual, the index
.
As usual, the index 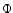 in Eq. (B.19) denotes a derivative
at constant
in Eq. (B.19) denotes a derivative
at constant 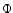 .
Similarly, for the momentum-derivatives we have
.
Similarly, for the momentum-derivatives we have
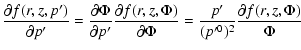 |
|
|
(B.20) |
and consequently
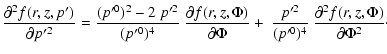 |
|
|
(B.21) |
Now, using Eq. (B.19) and collecting all terms together in
the transport Eq. (B.16) which depend on
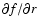 and additionally recalling that
and additionally recalling that
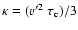 we may arrive at
we may arrive at
![$\displaystyle \left[\frac{1}{r}+\frac{\partial\kappa/\partial r}{\kappa}\right]...
...rac{\gamma^2~\Omega^2~r}{c^2}
\left(\frac{\partial f}{\partial r}\right)_{\Phi}$](/articles/aa/full/2002/48/aa2486/img175.gif) |
|
|
(B.22) |
where the position and momentum dependence of the collision
time
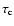 (and thus of the diffusion coefficient) has been
caught into the definition of the variables
(and thus of the diffusion coefficient) has been
caught into the definition of the variables 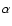 and
and 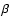 ,
i.e.
,
i.e. 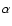 and
and 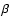 are given by
are given by
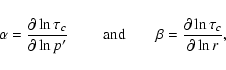 |
(B.23) |
respectively.
Equation (B.22) has been obtained noting that
v'2 = c2 p'2/(p'0)2 and
![$[\partial\tau_{\rm c}/\partial p']/\tau_{\rm c}
=\alpha/p'$](/articles/aa/full/2002/48/aa2486/img178.gif) and using
and using
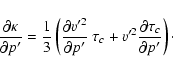 |
(B.24) |
In a similar manner, the terms depending on
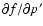 in Eq. (B.16) may be rewritten using
Eq. (B.20) as
in Eq. (B.16) may be rewritten using
Eq. (B.20) as
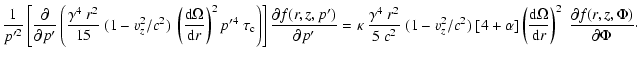 |
|
|
(B.25) |
Likewise, for the terms in Eq. (B.16) which depend
on
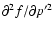 one finds
one finds
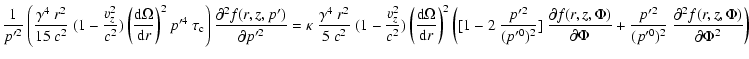 |
|
|
(B.26) |
where Eq. (B.21) has been used.
Now, collecting all relevant terms together the steady state transport
Eq. (B.16) may finally be rewritten as
with
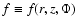 and where the r-derivatives
should be understood as derivatives keeping
and where the r-derivatives
should be understood as derivatives keeping 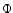 constant, i.e.
we may treat
constant, i.e.
we may treat 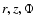 as independent variables.
Again, for vz=0 the partial differential equation
(B.27) reduces to the steady state transport equation
given in WJM 94 (e.g. see their Eq. (5.5)).
as independent variables.
Again, for vz=0 the partial differential equation
(B.27) reduces to the steady state transport equation
given in WJM 94 (e.g. see their Eq. (5.5)).
For the present application where we are interested in highly
relativistic particles with
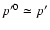 ,
the steady-state transport
Eq. (B.27) simplifies to
,
the steady-state transport
Eq. (B.27) simplifies to


Up: Particle acceleration in rotating
Copyright ESO 2002
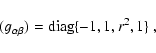
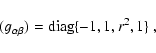
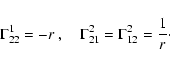
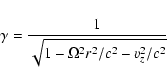
![]() the covariant
derivative is given by
the covariant
derivative is given by
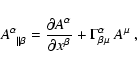
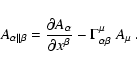
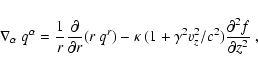
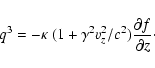
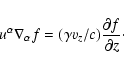
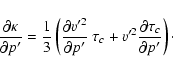
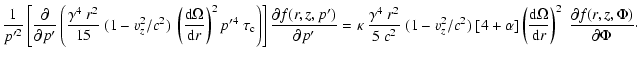
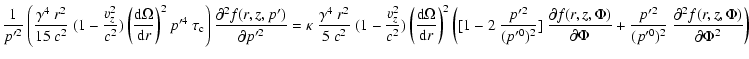
![]() ,
the steady-state transport
Eq. (B.27) simplifies to
,
the steady-state transport
Eq. (B.27) simplifies to