Up: Particle acceleration in rotating
Appendix A: The general steady state transport in the diffusion
approximation
In the case where we are concerned with the scattering of particles in
relativistic bulk flows, it has been typically found useful to evaluate
the scattering operator in the local Lorentz frame in which the fluid is
at rest, i.e. in the so-called comoving frame K'
(e.g. Webb 1985; Riffert 1986; Kirk et al. 1988)![[*]](/icons/foot_motif.gif) .
For in this frame K', a simple form of the scattering operator could be
applied if one assumes, as in the present approach, the rest frame of
the scattering centres to be essentially that of the background flow.
Quantities, which are operated upon the scattering operator, e.g. the
momentum, might then conveniently be evaluated in this comoving frame,
while the time and space coordinates are still measured in the laboratory
frame K characterized by its metric tensor
.
For in this frame K', a simple form of the scattering operator could be
applied if one assumes, as in the present approach, the rest frame of
the scattering centres to be essentially that of the background flow.
Quantities, which are operated upon the scattering operator, e.g. the
momentum, might then conveniently be evaluated in this comoving frame,
while the time and space coordinates are still measured in the laboratory
frame K characterized by its metric tensor
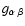 .
We would like to note however, that K' will in general be a
non-inertial coordinate system (i.e. an accelerated frame) and
therefore the related connection coefficients will not vanish.
With reference to the considered particle transport, the covariant
form of the Boltzmann equation is thus required, which may be achieved
by replacing the ordinary (partial) space-time derivatives by their
covariant derivatives.
Now, by starting from the relativistic Boltzmann equation and
by using a perturbation solution of the moment equations in the
diffusion approximation, i.e. by assuming the deviation of the
particle distribution from isotropy in the comoving frame to be small,
Webb (1989) has derived the general equation describing steady
state particle transport in relativistic rotating and shearing flows.
Following Eq. (4.4) of Webb (1989), the special relativistic
diffusive particle transport equation for the isotropic, mean scattering
frame distribution (averaged over all momentum directions)
.
We would like to note however, that K' will in general be a
non-inertial coordinate system (i.e. an accelerated frame) and
therefore the related connection coefficients will not vanish.
With reference to the considered particle transport, the covariant
form of the Boltzmann equation is thus required, which may be achieved
by replacing the ordinary (partial) space-time derivatives by their
covariant derivatives.
Now, by starting from the relativistic Boltzmann equation and
by using a perturbation solution of the moment equations in the
diffusion approximation, i.e. by assuming the deviation of the
particle distribution from isotropy in the comoving frame to be small,
Webb (1989) has derived the general equation describing steady
state particle transport in relativistic rotating and shearing flows.
Following Eq. (4.4) of Webb (1989), the special relativistic
diffusive particle transport equation for the isotropic, mean scattering
frame distribution (averaged over all momentum directions)
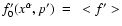 may be written as
may be written as
![$\displaystyle \frac{1}{p'^2} \frac{\partial}{\partial p'}
\left[-\frac{p'^3~c}{...
...al p'}\right]
+ \nabla_{\alpha}\left(c~u^{~\alpha}~f_0'+ q^{~\alpha}\right)= 0,$](/articles/aa/full/2002/48/aa2486/img104.gif) |
|
|
(A.1) |
with
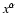 the position four vector in the laboratory
frame K, where the background plasma is in motion with four velocity
the position four vector in the laboratory
frame K, where the background plasma is in motion with four velocity
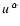 ,
and p'=m' v' the (magnitude of the) particle
momentum as measured in the local (comoving) fluid frame K'. Note,
that in order to simplify matters, the subscript 0 and the prime superscript are
omitted in
the following characterisations of the isotropic part of the particle
distribution function, i.e. f now denotes the isotropic part!
The total particle energy and momentum in the frame K' may be written
as
,
and p'=m' v' the (magnitude of the) particle
momentum as measured in the local (comoving) fluid frame K'. Note,
that in order to simplify matters, the subscript 0 and the prime superscript are
omitted in
the following characterisations of the isotropic part of the particle
distribution function, i.e. f now denotes the isotropic part!
The total particle energy and momentum in the frame K' may be written
as
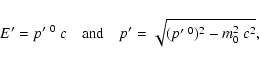 |
(A.2) |
respectively, with m0 the rest mass of the particle and
c the speed of light.
The terms in the first line of Eq. (A.1) represent particle
energy changes due to adiabatic expansion or compression of the flow
(i.e. the term proportional to the fluid four divergence
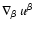 ), due to shear energization (i.e. the term
involving
), due to shear energization (i.e. the term
involving 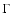 )
and due to the fact that K' is an accelerated
frame (i.e. the term
)
and due to the fact that K' is an accelerated
frame (i.e. the term
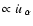 ,
cf. also
Webb 1985).
The second line gives the effects of diffusion and convection.
In Eq. (A.1),
,
cf. also
Webb 1985).
The second line gives the effects of diffusion and convection.
In Eq. (A.1),
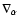 denotes the covariant
derivative while
denotes the covariant
derivative while
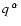 denotes the heat flux. This heat flux
contains a diffusive particle current plus a relativistic heat
inertial term
denotes the heat flux. This heat flux
contains a diffusive particle current plus a relativistic heat
inertial term 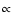
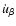 and is given by
and is given by
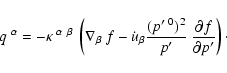 |
(A.3) |
As shown by Webb (1989), Eq. (A.1) could be regarded
as the relativistic generalization of the non-relativistic particle
transport equation first derived by Earl et al. (1988).
The acceleration four vector
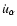 of the comoving
(or scattering) frame in Eqs. (A.1) and (A.3),
is defined by
of the comoving
(or scattering) frame in Eqs. (A.1) and (A.3),
is defined by
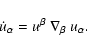 |
(A.4) |
The fluid energization coefficient 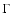 in Eq. (A.1)
represents energy changes due to viscosity. Since the acceleration
of particles draws energy from the fluid flow field, one expects on the
other hand the flow to be influenced by the presence of these
particles. As was shown, for example, by Earl et al. (1988) and Katz (1991), the resultant
dynamical effect on the flow could be modelled by means of an (induced)
viscosity coefficient. If one considers
the strong scattering limit, i.e. the case where
in Eq. (A.1)
represents energy changes due to viscosity. Since the acceleration
of particles draws energy from the fluid flow field, one expects on the
other hand the flow to be influenced by the presence of these
particles. As was shown, for example, by Earl et al. (1988) and Katz (1991), the resultant
dynamical effect on the flow could be modelled by means of an (induced)
viscosity coefficient. If one considers
the strong scattering limit, i.e. the case where
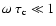 ,
with
,
with 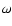 the gyrofrequency of the particle in the scattering frame
(i.e.
the gyrofrequency of the particle in the scattering frame
(i.e.
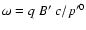 ),
),
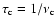 the mean time
interval between two scattering events and
the mean time
interval between two scattering events and
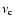 the collision
frequency, this fluid energization coefficient could be written as
(Webb 1989, Eq. (34))
the collision
frequency, this fluid energization coefficient could be written as
(Webb 1989, Eq. (34))
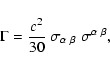 |
(A.5) |
where
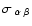 is the (covariant) fluid shear
tensor given by
is the (covariant) fluid shear
tensor given by
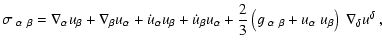 |
|
|
(A.6) |
with
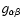 the (covariant) metric tensor.
Additionally, for the strong scattering limit the spatial diffusion
tensor
the (covariant) metric tensor.
Additionally, for the strong scattering limit the spatial diffusion
tensor
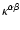 reduces to a simple form given by
reduces to a simple form given by
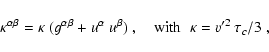 |
(A.7) |
the isotropic diffusion coefficient and v' the comoving particle
speed.


Up: Particle acceleration in rotating
Copyright ESO 2002
![$\displaystyle \frac{1}{p'^2} \frac{\partial}{\partial p'}
\left[-\frac{p'^3~c}{...
...al p'}\right]
+ \nabla_{\alpha}\left(c~u^{~\alpha}~f_0'+ q^{~\alpha}\right)= 0,$](/articles/aa/full/2002/48/aa2486/img104.gif)