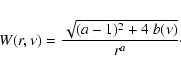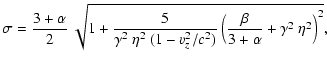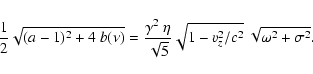Up: Particle acceleration in rotating
Subsections
For general applications one may search for (two-dimensional) Green's
solutions of the steady state transport equation (see also WJM 94), i.e.
solutions of Eq. (B.28) with source term
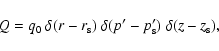 |
(C.1) |
or equivalently (i.e. utilizing the properties of the delta
function) with source term
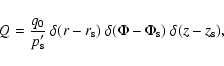 |
(C.2) |
describing monoenergetic injection of particles with momentum
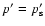 at position
at position
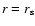 ,
,
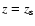 .
For consistency, the constant q0 in Eqs. (C.1) and
(C.2) has to be defined such, that the relevant expression
satisfies the requirement that
.
For consistency, the constant q0 in Eqs. (C.1) and
(C.2) has to be defined such, that the relevant expression
satisfies the requirement that
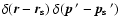 vanishes unless
vanishes unless
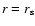 ,
,
 ,
,
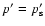 and integrate to unity (or
and integrate to unity (or 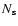 if
if 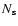 particles are
injected) over all space and momentum directions.
Using cylindrical coordinates this requires
particles are
injected) over all space and momentum directions.
Using cylindrical coordinates this requires
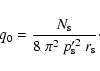 |
(C.3) |
Solutions of the transport Eq. (B.28) may
then be found by applying Fourier techniques, i.e. by using the double
Fourier transform defined by
![$\displaystyle F(r;\mu,\nu)=\int_{-\infty}^{\infty} {\rm d}z
\int_{-\infty}^{\infty} {\rm d}\Phi\;
\exp[i~(\nu~\Phi+\mu~z)]\;f(r,z,\Phi),$](/articles/aa/full/2002/48/aa2486/img194.gif) |
|
|
(C.4) |
where the inverse Fourier transform is given by
![$\displaystyle f(r, z, \Phi)=\frac{1}{4\pi^2}
\int_{-\infty}^{\infty}{\rm d}\mu\;\int_{-\infty}^{\infty}
{\rm d}\nu\;\exp[-i~(\nu~\Phi+\mu~z)]
F(r;\mu,\nu).$](/articles/aa/full/2002/48/aa2486/img195.gif) |
|
|
(C.5) |
Denoting the Fourier transform of the source term 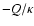 by
by
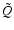 ,
we have
,
we have
Taking the Fourier transform of the transport
Eq. (B.28) one arrives at
![$\displaystyle \frac{\partial^2 F}{\partial r^2}+\left(\frac{1+\beta}{r}+[3+\alp...
...~v_z}{\kappa}~i~\mu
+ (1+\gamma^2\frac{v_z^2}{c^2})~\mu^2\right] F
=\tilde{Q}~.$](/articles/aa/full/2002/48/aa2486/img201.gif) |
|
|
(C.7) |
Let 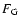 be the (two-dimensional) Green's solution of this equation
satisfying homogeneous, i.e. zero Dirichlet boundary conditions, then
Fourier inversion [i.e. Eq. (C.5)] yields the required
Green's function solution
be the (two-dimensional) Green's solution of this equation
satisfying homogeneous, i.e. zero Dirichlet boundary conditions, then
Fourier inversion [i.e. Eq. (C.5)] yields the required
Green's function solution
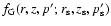 .
Generally, the considered Fourier techniques yield the Green's function
for infinite domains. The proper Green's function for bounded domains
(i.e. for finite z) may be obtained, for example, by the method of
images (e.g. Morse & Feshbach 1953, pp. 812-816) in
the case where the boundaries are restricted to straight lines in two
dimensions or planes in three dimensions. The steady state version
of the Green's formula (cf. WJM 94, Eqs. (3.24) and (7.12)) may then be
applied in order to arrive at the general solution of the considered
transport equation.
.
Generally, the considered Fourier techniques yield the Green's function
for infinite domains. The proper Green's function for bounded domains
(i.e. for finite z) may be obtained, for example, by the method of
images (e.g. Morse & Feshbach 1953, pp. 812-816) in
the case where the boundaries are restricted to straight lines in two
dimensions or planes in three dimensions. The steady state version
of the Green's formula (cf. WJM 94, Eqs. (3.24) and (7.12)) may then be
applied in order to arrive at the general solution of the considered
transport equation.
Yet, even for the simplification vz=0 and
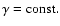 (i.e. using a simple galactic rotation law
(i.e. using a simple galactic rotation law
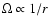 ), the
Green's function solution for the steady state transport
Eq. (B.28) is not straightforward to evaluate
(see WJM 94).
However, as we are primarily interested in an analysis of the azimuthal
effects of particle acceleration in rotating jet flows, we may be content
with a z-independent solution of the transport equation, i.e. with
an investigation of the so-called one-dimensional Green's function which
preserves much of the physics involved (cf. Morse &
Feshbach 1953, pp. 842-847).
This (one-dimensional) Green's function may be found by integrating the
two-dimensional ring source Q (which depends on the space coordinates
), the
Green's function solution for the steady state transport
Eq. (B.28) is not straightforward to evaluate
(see WJM 94).
However, as we are primarily interested in an analysis of the azimuthal
effects of particle acceleration in rotating jet flows, we may be content
with a z-independent solution of the transport equation, i.e. with
an investigation of the so-called one-dimensional Green's function which
preserves much of the physics involved (cf. Morse &
Feshbach 1953, pp. 842-847).
This (one-dimensional) Green's function may be found by integrating the
two-dimensional ring source Q (which depends on the space coordinates
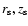 )
from
)
from
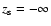 to
to
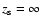 ;
i.e. the one-dimensional
Green's function represents the Green's solution for a steady state
monoenergetic injection of particles from a infinite cylindrical surface
parallel to the jet axis at radius
;
i.e. the one-dimensional
Green's function represents the Green's solution for a steady state
monoenergetic injection of particles from a infinite cylindrical surface
parallel to the jet axis at radius 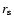 .
Hence, by utilizing the fourier
integral theorem it could be directly shown, that the one-dimensional Green's
function
.
Hence, by utilizing the fourier
integral theorem it could be directly shown, that the one-dimensional Green's
function
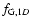 corresponds to a z-independent solution of the transport
Eq. (B.28) with source term
corresponds to a z-independent solution of the transport
Eq. (B.28) with source term
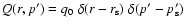 ,
i.e. the (one-dimensional)
Green's function we are seeking for in the following analysis, represents
the solution of the modified transport equation
,
i.e. the (one-dimensional)
Green's function we are seeking for in the following analysis, represents
the solution of the modified transport equation
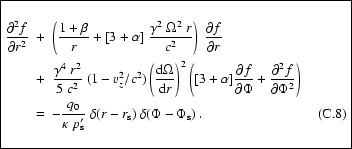
In the case of solid body (uniform) rotation shearing in the
background flow is absent since the fluid moves without internal
distortions.
For
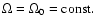 ,
Eq. (C.8)
reduces to the purely spatial transport equation
,
Eq. (C.8)
reduces to the purely spatial transport equation
![$\displaystyle \frac{\partial^2 f}{\partial r^2}+\left[\frac{1+\beta}{r}+ (3+\al...
...^2}{(1-\tilde{\Omega}_0^2~r^2/c^2)}
\right]~
\frac{\partial f}{\partial r}=Q_0,$](/articles/aa/full/2002/48/aa2486/img212.gif) |
|
|
(C.9) |
where the constant
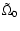 is defined by
is defined by
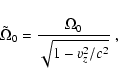 |
(C.10) |
while
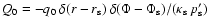 ,
with q0 given by Eq. (C.3), and
where the diffusion coefficient is assumed to be of the form
,
with q0 given by Eq. (C.3), and
where the diffusion coefficient is assumed to be of the form
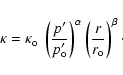 |
(C.11) |
with
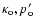 and
and
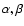 as constants,
cf. Eqs. (A.7) and (B.23).
as constants,
cf. Eqs. (A.7) and (B.23).
For rigid rotation Eq. (B.18) yields
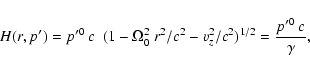 |
(C.12) |
where 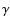 denotes the Lorentz factor of the flow.
As
denotes the Lorentz factor of the flow.
As
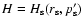 is a constant of motion (cf. Noether's theorem,
see also WJM 94), the particle momentum p' in the comoving frame
could be simply expressed as a function of the radial coordinate
is a constant of motion (cf. Noether's theorem,
see also WJM 94), the particle momentum p' in the comoving frame
could be simply expressed as a function of the radial coordinate
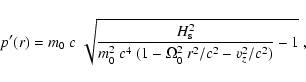 |
(C.13) |
with m0 the rest mass of the particle.
Basically, the solution space of the homogeneous part of
Eq. (C.9) could be described by a set of two
independent solutions, e.g. by the functions y1(r) and y2(r)
with Wronskian
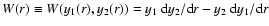 ,
where for an appropriate choice
,
where for an appropriate choice
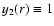 .
The relevant analytical expressions might be directly written down
for some special cases of interest:
.
The relevant analytical expressions might be directly written down
for some special cases of interest:
a.) for a constant diffusion
coefficient, i.e.
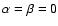 ,
two independent solutions are given
by
,
two independent solutions are given
by
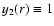 and
and
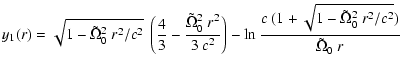 |
|
|
(C.14) |
where for the Wronskian one simply finds
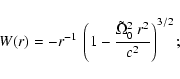 |
(C.15) |
b.) in the case, where 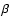 is negative, the solution y1(r) could
be expressed in terms of the incomplete Beta function (cf. Abramowitz &
Stegun 1965, p. 263), i.e. one finally may arrive at the
system
is negative, the solution y1(r) could
be expressed in terms of the incomplete Beta function (cf. Abramowitz &
Stegun 1965, p. 263), i.e. one finally may arrive at the
system
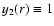 and
and
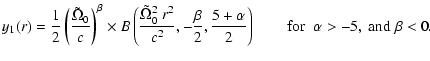 |
|
|
(C.16) |
Note, that now the solutions y1, y2 have been defined such that the
appropriate Wronskian reduces to Eq. (C.15) for
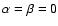 ,
i.e. we have
,
i.e. we have
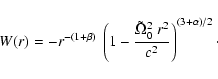 |
(C.17) |
The general (one-dimensional Green's) solution of the inhomogeneous
differential equation Eq. (C.9) with monoenergetic
source term Q0 defined above could then be written as (e.g. Morse
& Feshbach 1953, p. 530)
![$\displaystyle f(r,p')= y_1(r)~
\left[k_1 -\int^r \frac{Q_0~y_2(r)}{W(r)}\mbox{d}r \right]
+y_2(r)~\left[k_2 +\int^r \frac{Q_0~y_1(r)}{W(r)}
\mbox{d}r \right],$](/articles/aa/full/2002/48/aa2486/img229.gif) |
|
|
(C.18) |
where k1, k2 are integration constants specified by the
boundary conditions.
In the disk-jet scenario the accretion disk is usually assumed to
supply the mass for injection into the jet, thus for simplicity one
may consider a rather hollow jet structure (cf. Marcowith et
al. 1995; Fendt 1997a; Subramanian et
al. 1999) where the plasma motion in the azimuthal
direction is restricted to a region
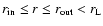 where
where
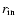 denotes the jet inner radius,
denotes the jet inner radius,
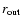 the relevant outer radius and
the relevant outer radius and 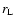 the light
cylinder radius.
Particles are supposed to be injected at position
the light
cylinder radius.
Particles are supposed to be injected at position 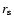 with initial momentum
with initial momentum
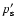 ,
where
,
where
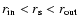 .
By chosing homogeneous boundary conditions
.
By chosing homogeneous boundary conditions
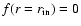 and
and
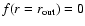 ,
the integration
constants in Eq. (C.18) are determined by
,
the integration
constants in Eq. (C.18) are determined by
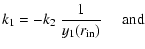 |
|
|
|
![$\displaystyle k_2=\frac{\tilde{q}~~[y_1(r_{\rm out})-y_1(r_{\rm s})]}
{1-y_1(r_{\rm out})/y_1(r_{\rm in})}~,$](/articles/aa/full/2002/48/aa2486/img236.gif) |
|
|
(C.19) |
where
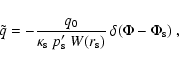 |
(C.20) |
with q0 given by Eq. (C.3), i.e.
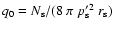 .
.
Therefore the (one-dimensional) Green's solution may be written as
![$\displaystyle f(r,p';r_{\rm s},p_{\rm s}')= y_1(r)~\left[k_1~\theta(r-r_{\rm s})+k_1~
\theta(r_{\rm s}-r) -\tilde{q}~\theta(r-r_{\rm s})\right]$](/articles/aa/full/2002/48/aa2486/img239.gif) |
|
|
|
![$\displaystyle \qquad
+\left[k_2~\theta(r-r_{\rm s})+k_2~\theta(r_{\rm s}
-r)+ \tilde{q}~y_1(r_{\rm s})~\theta(r-r_{\rm s})\right]~,$](/articles/aa/full/2002/48/aa2486/img240.gif) |
|
|
(C.21) |
where 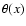 denotes the Heaviside step function.
The delta function in Eqs. (C.20) and (C.21)
indicates that the particle momentum in the comoving frame is directly
related to the relevant radial position by Eq. (C.13).
In order to gain insight into the efficiency of the acceleration process
one may introduce a spatial weighting function N(r) defined
by
denotes the Heaviside step function.
The delta function in Eqs. (C.20) and (C.21)
indicates that the particle momentum in the comoving frame is directly
related to the relevant radial position by Eq. (C.13).
In order to gain insight into the efficiency of the acceleration process
one may introduce a spatial weighting function N(r) defined
by
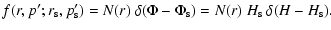 |
|
|
(C.22) |
In the case of Keplerian rotating background flow with
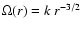 ,
,
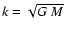 generally both, shear and centrifugal
acceleration, will occur.
By applying a simple Fourier transformation
(cf. Eqs. (C.4) and (C.5)), i.e.
generally both, shear and centrifugal
acceleration, will occur.
By applying a simple Fourier transformation
(cf. Eqs. (C.4) and (C.5)), i.e.
![\begin{displaymath}
F=\int_{-\infty}^{\infty}\mbox{d}\Phi~ \exp[i~\nu~\Phi]~f~,
\end{displaymath}](/articles/aa/full/2002/48/aa2486/img243.gif) |
(C.23) |
where the inverse Fourier transform is given by
![\begin{displaymath}f=\frac{1}{2~\pi} \int_{-\infty}^{\infty} \mbox{d}\nu~
\exp[-i~\nu~\Phi]~F~,
\end{displaymath}](/articles/aa/full/2002/48/aa2486/img244.gif) |
(C.24) |
the transport equation (C.8) could be
written as
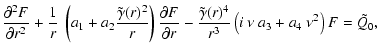 |
|
|
(C.25) |
where
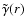 is defined by
is defined by
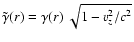 ,
with
,
with 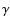 the Lorentz factor of the
flow, and where
the Lorentz factor of the
flow, and where
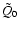 denotes the Fourier transform of the source
term
denotes the Fourier transform of the source
term
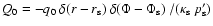 ,
i.e.
,
i.e.
![\begin{displaymath}
\tilde{Q}_0=-\frac{q_0~\exp[i~\nu~\Phi_{\rm s}]}{\kappa_{\rm s}~p_{\rm s}'}
~\delta(r-r_{\rm s})~.
\end{displaymath}](/articles/aa/full/2002/48/aa2486/img250.gif) |
(C.26) |
The abbreviations
a1, a2, a3, a4 in
Eq. (C.25) are defined by
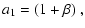 |
|
|
(C.27) |
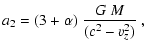 |
|
|
(C.28) |
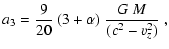 |
|
|
(C.29) |
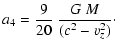 |
|
|
(C.30) |
An analytical evaluation of Eq. (C.25)
is rather complicated. However, a simple set of solutions may be
found in the case of r being large such that the rotational velocity
becomes non-relativistic and the approximation
![$\tilde{\gamma}(r)=
(1-G~M/[(c^2-v_z^2)~r])^{-1/2} \simeq 1 $](/articles/aa/full/2002/48/aa2486/img255.gif) holds. For, the Fourier
transformed transport equation then simplifies to
holds. For, the Fourier
transformed transport equation then simplifies to
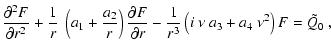 |
|
|
(C.31) |
which, using the substitution y=a2/r,
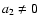 (i.e.
(i.e.
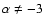 ), leads to
), leads to
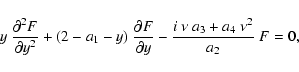 |
(C.32) |
for the homogeneous part of Eq. (C.31).
Equation (C.32) is known in the literature as Kummer's equation
(e.g. Abramowitz & Stegun 1965, p. 504).
For the general case where
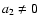 and
and
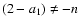 ,
,
 ,
the complete solution of this equation, i.e. of
the homogeneous part of Eq. (C.31),
may be written as
,
the complete solution of this equation, i.e. of
the homogeneous part of Eq. (C.31),
may be written as
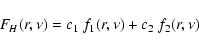 |
(C.33) |
where the functions f1, f2 are given by
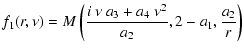 |
|
|
(C.34) |
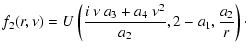 |
|
|
(C.35) |
Here, M(a,b,y) and U(a,b,y) denote the confluent hypergeometric
functions (cf. Abramowitz & Stegun 1965, pp. 504f;
Buchholz 1953, pp. 1-9), with M(a,b,y) being characterized
by the series representation
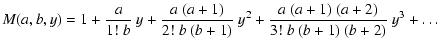 |
|
|
(C.36) |
while U(a,b,y) is given by the series
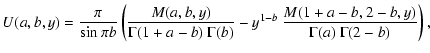 |
|
|
(C.37) |
with 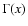 the Gamma function.
M(a,b,z) has a simple pole at b=-n for
the Gamma function.
M(a,b,z) has a simple pole at b=-n for 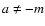 or for
a=-m if m>n, and is undefined for b=-n, a=-m and
or for
a=-m if m>n, and is undefined for b=-n, a=-m and 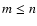 .
U(a,b,z), however, is defined even for
.
U(a,b,z), however, is defined even for
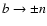 .
For the relevant Wronskian one has (e.g. Abramowitz & Stegun
1965, p. 505)
.
For the relevant Wronskian one has (e.g. Abramowitz & Stegun
1965, p. 505)
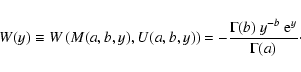 |
(C.38) |
Thus, for the Wronskian
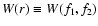 we find
we find
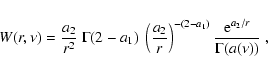 |
(C.39) |
where
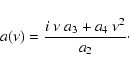 |
(C.40) |
For the general solution of the inhomogeneous fourier
equation (C.25) one finds
(cf. Eq. (C.18))
where
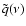 has been defined by
has been defined by
![\begin{displaymath}\tilde{q}(\nu)= - q_0~
\frac{\exp[i~\nu~\Phi_{\rm s}]}{\kappa_{\rm s} ~p_{\rm s}'~W(r_{\rm s},\nu)}~,
\end{displaymath}](/articles/aa/full/2002/48/aa2486/img279.gif) |
(C.42) |
with q0 given by Eq. (C.3) and where k1, k2 are
integration constants specified by the boundary conditions. For homogeneous
Dirichlet conditions at the boundaries
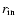 and
and
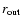 ,
i.e.
,
i.e.
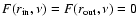 with
with
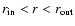 and
and
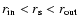 the integration constants are fixed
(for each
the integration constants are fixed
(for each 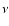 )
and given by
)
and given by
By Fourier inversion, we now may obtain the required (one-dimensional)
Green's function
![\begin{displaymath}
f(r,\Phi; r_{\rm s},\Phi_{\rm s})=\frac{1}{2~\pi}~\int_{-\infty}^{\infty}\mbox{d}\nu~
\exp[-i~\nu~\Phi]~F(r,\nu)~,
\end{displaymath}](/articles/aa/full/2002/48/aa2486/img287.gif) |
(C.45) |
with 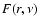 given by Eq. (C.41).
As may be obvious from the foregoing investigation this fourier
inversion is not easy to evaluate, not even using numerical methods.
However, in order to cope with the integration, we may consider the
following substitution (
given by Eq. (C.41).
As may be obvious from the foregoing investigation this fourier
inversion is not easy to evaluate, not even using numerical methods.
However, in order to cope with the integration, we may consider the
following substitution (
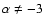 )
)
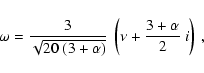 |
(C.46) |
for which one finds (cf. Eq. (C.40) and
Eqs. (C.27)-(C.30))
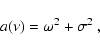 |
(C.47) |
where 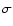 is defined by
is defined by
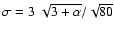 .
Performing the substitution in Eq. (C.45),
one arrives at an integral with the path of integration A
now in the complex plane, i.e. parallel to the real axis at a distance
.
Performing the substitution in Eq. (C.45),
one arrives at an integral with the path of integration A
now in the complex plane, i.e. parallel to the real axis at a distance
![$3~(3+\alpha)~i/[2~\sqrt{20~(3+\alpha)}~]$](/articles/aa/full/2002/48/aa2486/img293.gif) ,
extending from -R to
R with
,
extending from -R to
R with
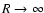 .
We may close the path by choosing a
rectangular contour C which consists of the stated parallel A, the
real axis, and the outer lines B1, B2 parallel to the imaginary
axis at R and -R, respectively. For the relevant ranges of
.
We may close the path by choosing a
rectangular contour C which consists of the stated parallel A, the
real axis, and the outer lines B1, B2 parallel to the imaginary
axis at R and -R, respectively. For the relevant ranges of 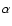 (
(
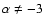 ;
;
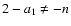 )
of interest, the integrand has no
poles within the region bounded by C and thus, by virtue of Cauchy's
integral theorem, the value of the contour integral around C sums to
zero. For
)
of interest, the integrand has no
poles within the region bounded by C and thus, by virtue of Cauchy's
integral theorem, the value of the contour integral around C sums to
zero. For
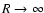 the integrals over B1 and over B2
vanish as might be verified by using asymptotic expansion formulas for the
integrand. Noting that by means of Euler's equation
the integrals over B1 and over B2
vanish as might be verified by using asymptotic expansion formulas for the
integrand. Noting that by means of Euler's equation
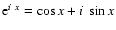 we have
we have
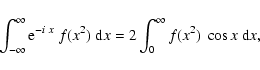 |
(C.48) |
and collecting all relevant expressions together, one
finally may arrive at the integral (
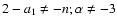 )
)
where we have introduced the following abbreviations
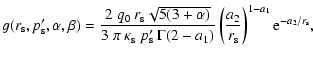 |
|
|
(C.51) |
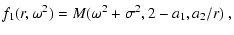 |
|
|
(C.52) |
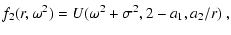 |
|
|
(C.53) |
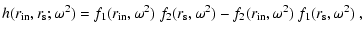 |
|
|
(C.54) |
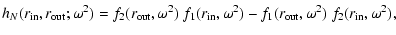 |
|
|
(C.55) |
with q0 given by Eq. (C.3).
Equation (C.49) may be evaluated using numerical methods
(cf. Wolfram 1996).
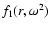 and
and
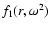 are bounded for
are bounded for
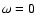 while the integrand
behaves well enough when
while the integrand
behaves well enough when
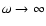 to allow for a
numerical evaluation.
to allow for a
numerical evaluation.
In the case of flat (galactic-type) rotation with
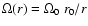 ,
the co-operation of centrifugal and shear
effects could be analysed more directly. Applying Fourier
transformation (cf. Eq. (C.23))
the transport Eq. (C.8)
simplifies to
,
the co-operation of centrifugal and shear
effects could be analysed more directly. Applying Fourier
transformation (cf. Eq. (C.23))
the transport Eq. (C.8)
simplifies to
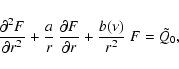 |
(C.56) |
where a and 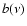 are defined by
are defined by
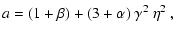 |
|
|
(C.57) |
![$\displaystyle b(\nu) = \left[(3+\alpha)~i~\nu + \nu^2 \right]
~\frac{\gamma^4~\eta^2}{5}~(1-v_z^2/c^2)$](/articles/aa/full/2002/48/aa2486/img315.gif) |
|
|
(C.58) |
with
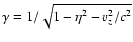 the Lorentz
factor of the flow and
the Lorentz
factor of the flow and
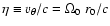 its rotational velocity, and where
its rotational velocity, and where
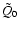 is given
by Eq. (C.26). Solutions for the homogeneous part
of Eq. (C.56) could then be directly
written down, i.e. one has
is given
by Eq. (C.26). Solutions for the homogeneous part
of Eq. (C.56) could then be directly
written down, i.e. one has
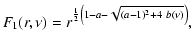 |
|
|
(C.59) |
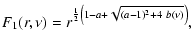 |
|
|
(C.60) |
with Wronskian 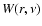 fixed by
fixed by
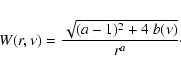 |
(C.61) |
The general solution of the inhomogeneous fourier
Eq. (C.56) in the case of homogeneous
Dirichlet conditions at the boundaries
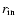 and
and
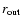 ,
may then be determined following the steps given in the previous
subsection, e.g. see Eqs. (C.41)-(C.45). In order to calculate the inverse Fourier
transform, it proves useful to apply the following substitutions
,
may then be determined following the steps given in the previous
subsection, e.g. see Eqs. (C.41)-(C.45). In order to calculate the inverse Fourier
transform, it proves useful to apply the following substitutions
 |
|
|
(C.62) |
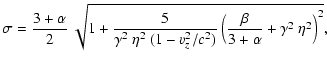 |
|
|
(C.63) |
for which one has
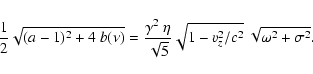 |
(C.64) |
The complete solution may then be found by proceeding as presented in
the previous subsection.


Up: Particle acceleration in rotating
Copyright ESO 2002
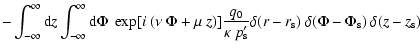
![]() (i.e. using a simple galactic rotation law
(i.e. using a simple galactic rotation law
![]() ), the
Green's function solution for the steady state transport
Eq. (B.28) is not straightforward to evaluate
(see WJM 94).
However, as we are primarily interested in an analysis of the azimuthal
effects of particle acceleration in rotating jet flows, we may be content
with a z-independent solution of the transport equation, i.e. with
an investigation of the so-called one-dimensional Green's function which
preserves much of the physics involved (cf. Morse &
Feshbach 1953, pp. 842-847).
This (one-dimensional) Green's function may be found by integrating the
two-dimensional ring source Q (which depends on the space coordinates
), the
Green's function solution for the steady state transport
Eq. (B.28) is not straightforward to evaluate
(see WJM 94).
However, as we are primarily interested in an analysis of the azimuthal
effects of particle acceleration in rotating jet flows, we may be content
with a z-independent solution of the transport equation, i.e. with
an investigation of the so-called one-dimensional Green's function which
preserves much of the physics involved (cf. Morse &
Feshbach 1953, pp. 842-847).
This (one-dimensional) Green's function may be found by integrating the
two-dimensional ring source Q (which depends on the space coordinates
![]() )
from
)
from
![]() to
to
![]() ;
i.e. the one-dimensional
Green's function represents the Green's solution for a steady state
monoenergetic injection of particles from a infinite cylindrical surface
parallel to the jet axis at radius
;
i.e. the one-dimensional
Green's function represents the Green's solution for a steady state
monoenergetic injection of particles from a infinite cylindrical surface
parallel to the jet axis at radius ![]() .
Hence, by utilizing the fourier
integral theorem it could be directly shown, that the one-dimensional Green's
function
.
Hence, by utilizing the fourier
integral theorem it could be directly shown, that the one-dimensional Green's
function
![]() corresponds to a z-independent solution of the transport
Eq. (B.28) with source term
corresponds to a z-independent solution of the transport
Eq. (B.28) with source term
![]() ,
i.e. the (one-dimensional)
Green's function we are seeking for in the following analysis, represents
the solution of the modified transport equation
,
i.e. the (one-dimensional)
Green's function we are seeking for in the following analysis, represents
the solution of the modified transport equation
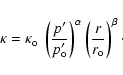
![]() ,
where for an appropriate choice
,
where for an appropriate choice
![]() .
The relevant analytical expressions might be directly written down
for some special cases of interest:
.
The relevant analytical expressions might be directly written down
for some special cases of interest:
![]() ,
two independent solutions are given
by
,
two independent solutions are given
by
![]() and
and
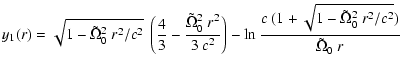
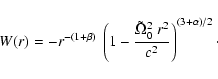
![]() where
where
![]() denotes the jet inner radius,
denotes the jet inner radius,
![]() the relevant outer radius and
the relevant outer radius and ![]() the light
cylinder radius.
Particles are supposed to be injected at position
the light
cylinder radius.
Particles are supposed to be injected at position ![]() with initial momentum
with initial momentum
![]() ,
where
,
where
![]() .
By chosing homogeneous boundary conditions
.
By chosing homogeneous boundary conditions
![]() and
and
![]() ,
the integration
constants in Eq. (C.18) are determined by
,
the integration
constants in Eq. (C.18) are determined by
![\begin{displaymath}f=\frac{1}{2~\pi} \int_{-\infty}^{\infty} \mbox{d}\nu~
\exp[-i~\nu~\Phi]~F~,
\end{displaymath}](/articles/aa/full/2002/48/aa2486/img244.gif)
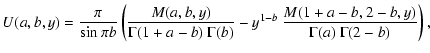
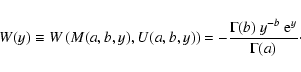
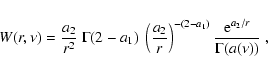
![\begin{displaymath}\tilde{q}(\nu)= - q_0~
\frac{\exp[i~\nu~\Phi_{\rm s}]}{\kappa_{\rm s} ~p_{\rm s}'~W(r_{\rm s},\nu)}~,
\end{displaymath}](/articles/aa/full/2002/48/aa2486/img279.gif)
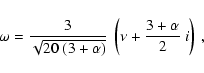
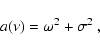
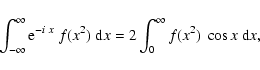
![$\displaystyle b(\nu) = \left[(3+\alpha)~i~\nu + \nu^2 \right]
~\frac{\gamma^4~\eta^2}{5}~(1-v_z^2/c^2)$](/articles/aa/full/2002/48/aa2486/img315.gif)