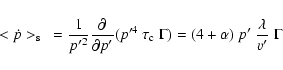 |
(9) |
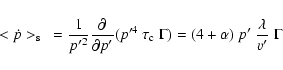 |
(9) |
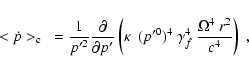 |
(10) |
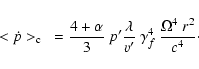 |
(11) |
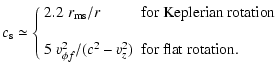 |
(12) |
Our approach utilises the relativistic diffusive particle
transport theory as advanced by Webb (1989) and Webb et al. (1994) and thus assumes the diffusion approximation to
be valid, i.e. the deviation of the particle distribution from isotropy
to be small. In a strict sense, this requires the particle mean free
path
![]() to be much smaller than both, the typical length
scale for the evolution of the mean (momentum-averaged) distribution
function and the typical length scale of variation for the background
flow. Our conclusions are therefore of restricted applicability if
highly anisotropic distributions are expected as, for example, near
ultra-relativistic shocks (cf. Kirk & Schneider 1987;
Kirk & Webb 1988).
to be much smaller than both, the typical length
scale for the evolution of the mean (momentum-averaged) distribution
function and the typical length scale of variation for the background
flow. Our conclusions are therefore of restricted applicability if
highly anisotropic distributions are expected as, for example, near
ultra-relativistic shocks (cf. Kirk & Schneider 1987;
Kirk & Webb 1988).
In the application presented here, energy changes as a result of radiative (e.g. synchrotron) losses or second-order Fermi effects due to stochastic motions of the scattering centres have not been considered. One expects the inclusion of radiative losses to introduce an upper bound to the possible particle energy at the point where acceleration is balanced by losses, thus leading to a cut-off in the particle momentum spectrum. On the other hand, the inclusion of second-order Fermi effects would give an additional diffusion flux in momentum space. It may formally be taken into account by a more careful treatment of the scattering term in the Boltzmann equation. For non-relativistic jet flows, a numerical study of second-order Fermi acceleration has recently been given by Manolakou et al. (1999). Our present omission of second-order Fermi acceleration in the relativistic transport equation appears justifiable for the cases where the typical random velocities of the scattering centres (as measured in the comoving frame, i.e. relative to the flow) are smaller than a product of the radial particle mean free path times the rotational flow velocity gradient. However, one should note, that estimating the effects of second-order Fermi acceleration for the case of flat rotation, for example, clearly show them to be of increasing relevance for decreasing azimuthal flow velocities. A more detailed analysis will thus be given in a subsequent publication, while the purpose of the present model is confined to the analysis of steady-state solutions and the essential physical features of shear and centrifugal acceleration.
So far, shear-type acceleration processes in the context of AGN jets
have been investigated by Subramanian et al. (1999) and
Ostrowski (1998, 2000):
By following the road suggested by Katz (1991), who considered
the particle acceleration in a low density corona due to flux tubes
anchored in a keplerian accretion disk, Subramanian et
al. (1999) investigated the acceleration of protons driven
by the shear of the underlying Keplerian accretion disk. They
demonstrated that the shear acceleration may transfer the energy
required for powering the jet and showed the shear to dominate over
second-order Fermi acceleration. However, their model does not deal
with the acceleration of particles emitting high energy radiation, but
is basically confined to the bulk acceleration of the jet flow up to
asymptotic Lorentz factors of ![]() 10.
On the other hand, Ostrowski (1998, 2000)
examined the acceleration of cosmic ray particles at a sharp tangential
flow discontinuity. He demonstrated that both, the acceleration to
very high energies as well as the production of flat particle spectra
are possible. In order for this model to apply efficiently, one
requires several conditions to be satisfied, including the presence of
a relativistic velocity difference and a thin (not extended) boundary,
as well as a sufficient amount of turbulence on both sides of the
boundary. It seems however that such conditions might be realized, for
example, at the jet side boundary layer in powerful FR II radio
sources.
With respect to shear acceleration, our approach can thus be regarded
as complementary to the one developed by Ostrowski. While our analysis
considers the influence of a gradual (azimuthal) shear profile in the
jet interior, the analysis by Ostrowski deals with a sharp tangential
shear profile at the jet boundary layer. Generally, one expects both
processes to occur and to contribute to the production of high energy
particles, their relative contributions being dependent on the
specific conditions realized in the jet interior and its boundary.
10.
On the other hand, Ostrowski (1998, 2000)
examined the acceleration of cosmic ray particles at a sharp tangential
flow discontinuity. He demonstrated that both, the acceleration to
very high energies as well as the production of flat particle spectra
are possible. In order for this model to apply efficiently, one
requires several conditions to be satisfied, including the presence of
a relativistic velocity difference and a thin (not extended) boundary,
as well as a sufficient amount of turbulence on both sides of the
boundary. It seems however that such conditions might be realized, for
example, at the jet side boundary layer in powerful FR II radio
sources.
With respect to shear acceleration, our approach can thus be regarded
as complementary to the one developed by Ostrowski. While our analysis
considers the influence of a gradual (azimuthal) shear profile in the
jet interior, the analysis by Ostrowski deals with a sharp tangential
shear profile at the jet boundary layer. Generally, one expects both
processes to occur and to contribute to the production of high energy
particles, their relative contributions being dependent on the
specific conditions realized in the jet interior and its boundary.
Copyright ESO 2002