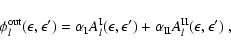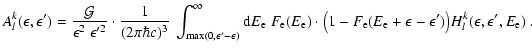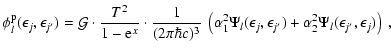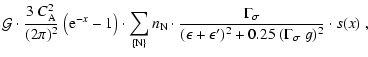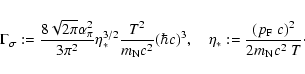Up: Radiation hydrodynamics with neutrinos
Subsections
Online Material
Appendix A: Neutrino opacities
In this appendix we shall describe the neutrino-matter interactions
that are included in the current version of our neutrino transport
code for supernova simulations. We shall focus on aspects which are
specific and important for their numerical handling and will present
final rate expressions in the form used in our code and with a
consistent notation.
Table A.1:
Overview of all neutrino-matter interactions currently
implemented in the code.
For each process we list the sections where we summarize fundamental
aspects of the
calculation of the corresponding rate and give details of its
numerical implementation.
The references point to papers where more information can be found
about the approximations employed in the rate calculations.
In the first column the symbol 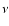 represents any of the neutrinos
represents any of the neutrinos
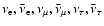 ,
the
symbols
,
the
symbols 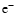 ,
,
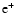 ,
,
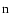 ,
,
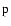 and A denote electrons, positrons,
free neutrons and protons, and heavy nuclei, respectively, the
symbol
and A denote electrons, positrons,
free neutrons and protons, and heavy nuclei, respectively, the
symbol 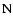 means
means 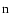 or
or 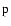 .
.
| Reaction |
|
|
Rate described in |
Reference |
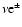 |
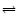 |
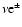 |
Sects. A.1.2, A.2.4 |
Mezzacappa & Bruenn (1993b); Cernohorsky (1994) |
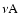 |
 |
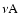 |
Sects. A.1.2, A.2.3 |
Horowitz (1997); Bruenn & Mezzacappa (1997) |
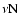 |
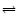 |
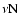 |
Sects. A.1.2, A.2.1 |
Bruenn (1985); Mezzacappa & Bruenn (1993c) |
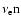 |
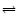 |
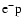 |
Sects. A.1.1, A.2.1 |
Bruenn (1985); Mezzacappa & Bruenn (1993c) |
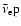 |
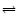 |
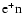 |
Sects. A.1.1, A.2.1 |
Bruenn (1985); Mezzacappa & Bruenn (1993c) |
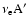 |
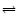 |
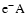 |
Sects. A.1.1, A.2.2 |
Bruenn (1985); Mezzacappa & Bruenn (1993c) |
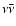 |
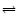 |
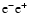 |
Sects. A.1.3, A.2.5 |
Bruenn (1985); Pons et al. (1998) |
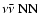 |
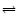 |
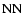 |
Sects. A.1.3, A.2.6 |
Hannestad & Raffelt (1998) |
In the following we discuss the different neutrino-matter interaction
processes which contribute to the source term
("collision integral'') on the rhs of the Boltzmann
equation:
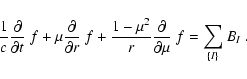 |
(A.1) |
The sum on the rhs of this equation runs over all
considered interaction processes
that can change the distribution function of a particular type of
neutrino. For simplicity we have written down the Boltzmann
equation for static media, here.
In the general case of a moving stellar fluid, velocity-dependent
terms have to appear on the lhs of Eq. (A.1) when the
neutrino quantities and the neutrino-matter interaction rates are
evaluated in the local rest frame of the fluid.
The phase-space distribution function f is
related to the
specific intensity 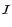 used in the main body of this paper by
used in the main body of this paper by
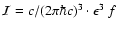 .
Accordingly, the source term on the rhs of the Boltzmann equation,
Eq. (6), and the corresponding moment equations for
neutrino number and
neutrino energy or momentum (Eqs. (30), (31),
(7), (8)) can be calculated from BI as
.
Accordingly, the source term on the rhs of the Boltzmann equation,
Eq. (6), and the corresponding moment equations for
neutrino number and
neutrino energy or momentum (Eqs. (30), (31),
(7), (8)) can be calculated from BI as
where
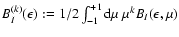 .
Here and in the following, the dependence of quantities on the
space-time coordinates (t,r) is suppressed in the notation.
Throughout Appendix A the temperature T is measured
in units of energy.
.
Here and in the following, the dependence of quantities on the
space-time coordinates (t,r) is suppressed in the notation.
Throughout Appendix A the temperature T is measured
in units of energy.
A.1.1 Neutrino absorption and emission
The rate of change (modulo a factor of 1/c) of the neutrino
distribution function due to absorption and emission processes
is given by (see Bruenn 1985)
![\begin{displaymath}
B_{\rm AE}(\epsilon,\mu)=
j(\epsilon)[1-f(\epsilon,\mu)]-f(\epsilon,\mu)/\lambda(\epsilon)
~,
\end{displaymath}](/articles/aa/full/2002/46/aa2451/img586.gif) |
(A.3) |
where j denotes the emissivity and 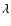 is the mean free
path for neutrino absorption.
The factor (1-f) accounts for fermion phase space
blocking effects of neutrinos.
Using the Kirchhoff-Planck relation ("detailed balance''), and
introducing the absorption opacity corrected for stimulated absorption,
is the mean free
path for neutrino absorption.
The factor (1-f) accounts for fermion phase space
blocking effects of neutrinos.
Using the Kirchhoff-Planck relation ("detailed balance''), and
introducing the absorption opacity corrected for stimulated absorption,
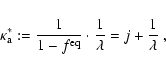 |
(A.4) |
Eq. (A.3) can be rewritten as
![\begin{displaymath}
B_{\rm AE}(\epsilon,\mu)=
\kappa_{\rm a}^*(\epsilon)[f^{\rm eq}(\epsilon)-f(\epsilon,\mu)]
~.
\end{displaymath}](/articles/aa/full/2002/46/aa2451/img588.gif) |
(A.5) |
In Eq. (A.5) it becomes evident that the source
term drives the neutrino distribution function
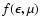 towards its equilibrium value
towards its equilibrium value
![$f^{\rm eq}(\epsilon)=(1+\exp{[(\epsilon-\mu_\nu^{\rm eq})/T]})^{-1}$](/articles/aa/full/2002/46/aa2451/img590.gif) ,
where
,
where
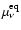 denotes the chemical potential for
neutrinos in thermodynamic equilibrium with the stellar medium.
In equilibrium, the source term vanishes in accordance with the
requirement of detailed balance.
denotes the chemical potential for
neutrinos in thermodynamic equilibrium with the stellar medium.
In equilibrium, the source term vanishes in accordance with the
requirement of detailed balance.
A.1.2 Scattering
The rate of change of the neutrino
distribution function due to
scattering of neutrinos off some target particles is
given by the collision integral (cf. Cernohorsky 1994, Eqs. (2.1), (2.3))
![$\displaystyle B_{\rm S}(\vec{q})=
\int
\frac{{\rm d}^3\vec{\vec{q'}}~}{(2\pi)^3...
...},\vec{q'})
-f_\nu(1-f'_\nu)\widetilde{R}^{\rm out}(\vec{q},\vec{q'})\right]
~,$](/articles/aa/full/2002/46/aa2451/img592.gif) |
|
|
(A.6) |
where 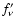 depends on
depends on 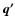 and
the scattering kernels
and
the scattering kernels
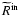 and
and
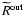 are defined as the following phase space
integrals over products of the transition rate
are defined as the following phase space
integrals over products of the transition rate 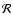 and
the Fermi distribution functions
and
the Fermi distribution functions 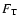 of the target particles:
of the target particles:
The vectors 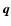 and
and 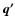 are the momenta of the ingoing and outgoing neutrinos, respectively,
and
are the momenta of the ingoing and outgoing neutrinos, respectively,
and 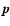 and
and 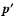 those of their scattering targets.
those of their scattering targets.
The scattering kernels are usually given as functions of the
energies 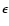 and
and 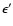 of the ingoing and outgoing neutrino
and the cosine
of the ingoing and outgoing neutrino
and the cosine
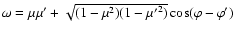 of
the scattering angle, where
of
the scattering angle, where
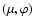 and
and
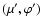 are
the corresponding momentum space coordinates.
Expanding the scattering kernels
(
are
the corresponding momentum space coordinates.
Expanding the scattering kernels
(
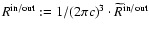 )
in a Legendre series
)
in a Legendre series
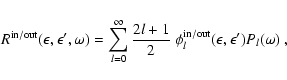 |
(A.8) |
with the Legendre coefficients
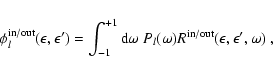 |
(A.9) |
and applying the addition theorem for Legendre polynomials
![$P_l(\omega)=P_l(\mu)P_l(\mu')+2\sum_{m=1}^{l}\frac{(l-m)!}{(l+m)!}P_l^m(\mu)P_l^m(\mu')\cos[m(\varphi-\varphi')]$](/articles/aa/full/2002/46/aa2451/img613.gif) (e.g., Bronstein & Semendjajew 1991, Plm are the associated Legendre polynomials),
the integral over
(e.g., Bronstein & Semendjajew 1991, Plm are the associated Legendre polynomials),
the integral over 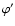 in the collision integral can
be performed analytically (Yueh & Buchler 1977; Schinder & Shapiro 1982).
For use in our Boltzmann transport code, it is necessary to truncate
the Legendre expansion at some level.
Note that the orthogonality relation
in the collision integral can
be performed analytically (Yueh & Buchler 1977; Schinder & Shapiro 1982).
For use in our Boltzmann transport code, it is necessary to truncate
the Legendre expansion at some level.
Note that the orthogonality relation
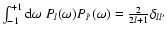 (e.g., Bronstein & Semendjajew 1991) implies that any truncation of the Legendre
series
(e.g., Bronstein & Semendjajew 1991) implies that any truncation of the Legendre
series
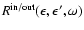 still gives the
exact integral value
still gives the
exact integral value
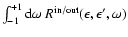 ,
independent of the level of truncation
,
independent of the level of truncation
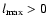 .
.
The collision integral and its first two angular moments finally
read![[*]](/icons/foot_motif.gif) :
:
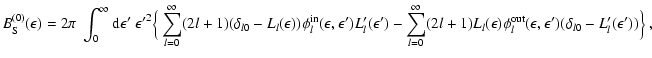 |
|
|
(A.11) |
![$\displaystyle B^{(1)}_{\rm S}(\epsilon) =
2\pi~\int_0^\infty {\rm d}\epsilon'~ ...
...on)]
\phi_l^{\rm out}(\epsilon,\epsilon')(\delta_{l0}-L'_l(\epsilon'))\Big\}
~,$](/articles/aa/full/2002/46/aa2451/img627.gif) |
|
|
(A.12) |
where the "Legendre moment''
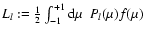 of order l
of the distribution function has been introduced.
These Legendre moments
can obviously be written as linear combinations
of the angular moments
of order l
of the distribution function has been introduced.
These Legendre moments
can obviously be written as linear combinations
of the angular moments
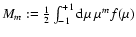 ,
which
occur in the formulation of the transport equations used in our
code.
Detailed balance requires
,
which
occur in the formulation of the transport equations used in our
code.
Detailed balance requires
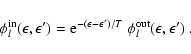 |
(A.13) |
Note that exploiting the in-out invariance of the transition rate
(and therefore
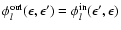 ;
e.g. Cernohorsky 1994) leads to
;
e.g. Cernohorsky 1994) leads to
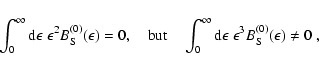 |
(A.14) |
which means that neutrino number is conserved in the scattering process,
whereas there is a nonvanishing energy exchange between neutrinos and
matter due to scatterings.
If for a particular
scattering process the energy transfer between neutrinos and
target particles
can be neglected, we have
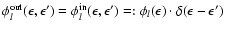 ,
and
the source terms given by Eqs. (A.10), (A.11),
(A.12)
simplify to
,
and
the source terms given by Eqs. (A.10), (A.11),
(A.12)
simplify to
A.1.3 Pair processes
Applying the procedures outlined in Sect. A.1.2
to the collision integral for the process of thermal emission and
absorption of neutrino-antineutrino pairs by electron positron
pairs and related reactions (e.g., nucleon-nucleon bremsstrahlung), the
corresponding source terms read (see Bruenn 1985; Pons et al. 1998):
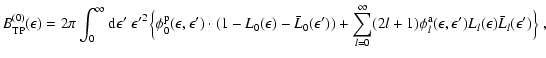 |
|
|
(A.19) |
![$\displaystyle B^{(1)}_{\rm TP}(\epsilon) =
2\pi\int_0^\infty {\rm d}\epsilon'~ ...
...n')
[
(l+1)L_{l+1}(\epsilon)+l L_{l-1}(\epsilon)
]\bar{L}_l(\epsilon')
\Big\}~.$](/articles/aa/full/2002/46/aa2451/img642.gif) |
|
|
(A.20) |
Here bars indicate quantities for antineutrinos.
The absorption and production kernels are related by
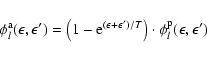 |
(A.21) |
in accordance with the requirement of detailed balance.
A.2 Numerical implementation of various interaction processes
In the following we describe the implementation of the various
neutrino-matter interactions into our transport scheme.
The expressions are mainly taken from the works of
Tubbs & Schramm (1975), Schinder & Shapiro (1982), Bruenn (1985), and Mezzacappa & Bruenn (1993b,c).
All average values of the source terms within individual energy bins
(cf. Eq. (20)) are approximated to zeroth
order by assuming the integrand to be a piecewise constant function of
the neutrino energy 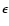 ,
and hence:
,
and hence:
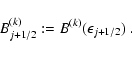 |
(A.22) |
With the rest-mass energy of the electron,
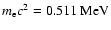 ,
and the
characteristic cross section of weak interactions
,
and the
characteristic cross section of weak interactions
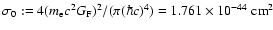 (
(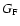 is Fermi's constant), we define:
is Fermi's constant), we define:
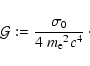 |
(A.23) |
A.2.1 Neutrino absorption, emission and scattering
by free
nucleons
In the standard description of neutrino-nucleon interactions
(see Tubbs & Schramm 1975; Bruenn 1985; Mezzacappa & Bruenn 1993c),
many-body effects for the nucleons in the dense medium, energy
transfer between leptons and nucleons as well as nucleon thermal
motions are ignored.
The corresponding simplifications allow for a straightforward
implementation of the processes, using Eq. (A.5) for the
charged-current reactions and
Eqs. (A.15)-(A.17) for the neutral-current
scatterings, respectively. Expressions for
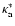 and the
Legendre coefficients
and the
Legendre coefficients
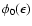 ,
,
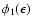 can be
computed from the rates given by Bruenn (1985) and Mezzacappa & Bruenn (1993c).
can be
computed from the rates given by Bruenn (1985) and Mezzacappa & Bruenn (1993c).
For absorption of electron neutrinos by free neutrons
(
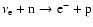 )
the final result for the opacity is:
)
the final result for the opacity is:
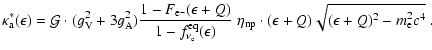 |
|
|
(A.24) |
The opacity of the absorption of
electron antineutrinos by free protons
(
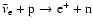 )
is
)
is
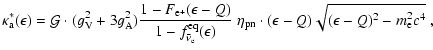 |
|
|
(A.25) |
if the neutrino energy
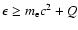 ,
and
,
and
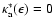 ,
else.
Here,
,
else.
Here,
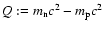 denotes the difference of the
rest-mass energies of the neutron and the proton, and
denotes the difference of the
rest-mass energies of the neutron and the proton, and
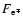 are the Fermi distribution functions of electrons or positrons.
The constants
are the Fermi distribution functions of electrons or positrons.
The constants
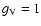 and
and
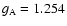 are the
nucleon form factors for the vector and axial vector currents, respectively.
The quantities
are the
nucleon form factors for the vector and axial vector currents, respectively.
The quantities
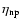 and
and
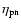 take into account the effects of fermion blocking of the nucleons.
Making the approximations mentioned above, in
particular ignoring the recoil of the nucleon,
Bruenn (1985, Eq. (C14); see also Reddy et al. 1998) derived:
take into account the effects of fermion blocking of the nucleons.
Making the approximations mentioned above, in
particular ignoring the recoil of the nucleon,
Bruenn (1985, Eq. (C14); see also Reddy et al. 1998) derived:
where 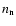 ,
,
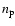 are the number densities
of neutrons and protons, respectively.
The corresponding degeneracy parameters
are the number densities
of neutrons and protons, respectively.
The corresponding degeneracy parameters
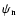 and
and
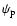 are calculated by inverting the relation (
are calculated by inverting the relation (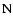 stands for
stands for 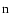 or
or 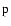 )
)
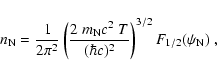 |
(A.27) |
where F1/2 is the Fermi integral of index 1/2 (see, e.g., Lattimer & Swesty 1991, Sect. 2.2).
The quantity
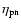 in Eq. (A.25) is defined
accordingly by exchanging the subscripts n and p in
Eq. (A.26).
In the nondegenerate
regime, where blocking is unimportant, one verifies the familiar limits
in Eq. (A.25) is defined
accordingly by exchanging the subscripts n and p in
Eq. (A.26).
In the nondegenerate
regime, where blocking is unimportant, one verifies the familiar limits
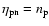 and
and
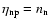 .
.
Scattering of neutrinos off free nucleons (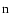 or
or 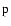 )
is mediated by neutral
currents only, which makes the distinction between neutrinos and
antineutrinos unneccessary.
Neglecting nucleon recoil and nucleon thermal motions, the
isoenergetic kernel obeys
)
is mediated by neutral
currents only, which makes the distinction between neutrinos and
antineutrinos unneccessary.
Neglecting nucleon recoil and nucleon thermal motions, the
isoenergetic kernel obeys
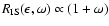 (e.g. Bruenn 1985; Mezzacappa & Bruenn 1993c), which implies
(e.g. Bruenn 1985; Mezzacappa & Bruenn 1993c), which implies
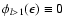 .
The non-vanishing Legendre coefficients read
.
The non-vanishing Legendre coefficients read
The factors
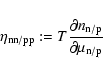 |
(A.30) |
approximately account for nucleon final state
blocking (Bruenn 1985), and
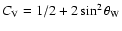 with
with
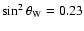 for the Weinberg angle.
In order to accurately reproduce the limits
for the Weinberg angle.
In order to accurately reproduce the limits
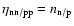 for nondegenerate (and nonrelativistic),
and
for nondegenerate (and nonrelativistic),
and
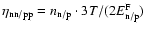 for degenerate (and nonrelativistic)
nucleons (
for degenerate (and nonrelativistic)
nucleons (
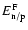 is the Fermi energy) we prefer using
the analytic interpolation formula proposed by Mezzacappa & Bruenn (1993c)
is the Fermi energy) we prefer using
the analytic interpolation formula proposed by Mezzacappa & Bruenn (1993c)
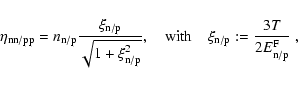 |
(A.31) |
instead of a direct numerical evaluation of Eq. (A.30).
A.2.2 Neutrino absorption and emission by heavy nuclei
As in the case of charged-current reactions with free nucleons,
neutrino absorption and emission by heavy nuclei
(
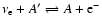 )
is implemented
by using Eq. (A.5).
For calculating the opacity of this process
we adopt the description employed by Bruenn (1985) and
Mezzacappa & Bruenn (1993c):
)
is implemented
by using Eq. (A.5).
For calculating the opacity of this process
we adopt the description employed by Bruenn (1985) and
Mezzacappa & Bruenn (1993c):
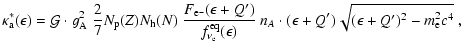 |
|
|
(A.32) |
if
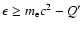 ,
and
,
and
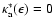 else.
Here
else.
Here
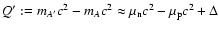 denotes the
energy difference between the excited state
A'=(N+1,Z-1) and the
ground state A=(N,Z).
Following Bruenn (1985), we set
denotes the
energy difference between the excited state
A'=(N+1,Z-1) and the
ground state A=(N,Z).
Following Bruenn (1985), we set 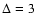 MeV for all nuclei.
The internal structure of the nucleus with charge Z and
neutron number N=A-Z is represented by the term
MeV for all nuclei.
The internal structure of the nucleus with charge Z and
neutron number N=A-Z is represented by the term
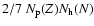 ,
with the functions
,
with the functions
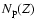 ,
,
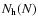 as given by Mezzacappa & Bruenn (1993c, Eqs. (31), (32)).
as given by Mezzacappa & Bruenn (1993c, Eqs. (31), (32)).
A.2.3 Coherent scattering of neutrinos off nuclei
We use reaction rates for coherent neutrino scatterings off nuclei
which include corrections due to the "nuclear form factor''
(following an approximation by Mezzacappa & Bruenn 1993c; Bruenn & Mezzacappa 1997), and
ion-ion correlations (as described in Horowitz 1997).
For a detailed discussion of the numerical handling of both
corrections, see the appendix of Bruenn & Mezzacappa
(1997). The result of the latter reference can readily be
used to calculate
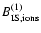 ,
the contribution of coherent
scattering to the rhs of the first order moment equation.
For the Boltzmann equation,
we have to make a minor additional approximation:
The correction factor
,
the contribution of coherent
scattering to the rhs of the first order moment equation.
For the Boltzmann equation,
we have to make a minor additional approximation:
The correction factor
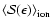 as provided by Horowitz (1997)
applies for the transport opacity and thus for the combination
as provided by Horowitz (1997)
applies for the transport opacity and thus for the combination
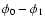 (which is given by Bruenn & Mezzacappa 1997) but not
necessarily for the
Legendre coefficients
(which is given by Bruenn & Mezzacappa 1997) but not
necessarily for the
Legendre coefficients 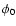 and
and 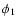 individually, which are
needed for calculating the collision integral
individually, which are
needed for calculating the collision integral
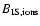 for
the Boltzmann equation.
We nevertheless assume here that
for
the Boltzmann equation.
We nevertheless assume here that
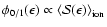 .
This implies
.
This implies
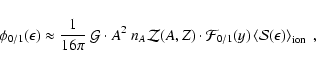 |
(A.33) |
with
containing the effects of the nuclear form factor, and
![\begin{displaymath}\mathcal{Z}(A,Z):=
\left[(C_{\rm A}-C_{\rm V})+(2-C_{\rm A}-C_{\rm V})\frac{2Z-A}{A}\right]^2
~\cdot
\end{displaymath}](/articles/aa/full/2002/46/aa2451/img708.gif) |
(A.35) |
 is defined as before (see Eqs. (A.28),
(A.29)) and
is defined as before (see Eqs. (A.28),
(A.29)) and
 .
In effect, the angular dependence of the ion-ion correlation correction
is not exactly accounted for in the Boltzmann equation.
The approximation, however, only influences the closure relation
for the moment equations at a higher level of accuracy.
It neither affects the Legendre coefficients at larger neutrino energies
(where
.
In effect, the angular dependence of the ion-ion correlation correction
is not exactly accounted for in the Boltzmann equation.
The approximation, however, only influences the closure relation
for the moment equations at a higher level of accuracy.
It neither affects the Legendre coefficients at larger neutrino energies
(where
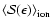 is
close to unity) nor
does it destroy the consistency of the Boltzmann equation and its
moment equations.
Moreover, it has been shown that the overall effect of
ion-ion correlations in stellar core collapse is only
marginally relevant (Bruenn & Mezzacappa 1997; Rampp 2000).
is
close to unity) nor
does it destroy the consistency of the Boltzmann equation and its
moment equations.
Moreover, it has been shown that the overall effect of
ion-ion correlations in stellar core collapse is only
marginally relevant (Bruenn & Mezzacappa 1997; Rampp 2000).
A.2.4 Inelastic scattering of neutrinos off charged leptons
For the scattering of neutrinos off charged leptons,
we approximate the dependence of the scattering kernel on the
scattering angle by truncating the Legendre expansions
(Eqs. (A.10)-(A.12)) at
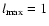 .
For our purposes, this has been shown to provide a sufficiently
accurate approximation (see Smit & Cernohorsky 1996; Mezzacappa & Bruenn 1993b), in
particular also because the total scattering rate is correctly
represented.
Expressions for the Legendre coefficients are taken from the
works of Yueh & Buchler (1977), Mezzacappa & Bruenn (1993b), Cernohorsky (1994), Smit & Cernohorsky (1996):
.
For our purposes, this has been shown to provide a sufficiently
accurate approximation (see Smit & Cernohorsky 1996; Mezzacappa & Bruenn 1993b), in
particular also because the total scattering rate is correctly
represented.
Expressions for the Legendre coefficients are taken from the
works of Yueh & Buchler (1977), Mezzacappa & Bruenn (1993b), Cernohorsky (1994), Smit & Cernohorsky (1996):
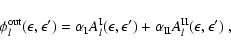 |
(A.36) |
with
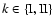 and
and
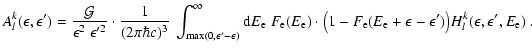 |
|
|
(A.37) |
The constants
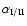 ,
which depend on the neutrino
species and also the type of charged lepton (i.e. electron or
positron) involved in the scattering process, are combinations of the
weak coupling constants (see, e.g., Cernohorsky 1994).
For the
,
which depend on the neutrino
species and also the type of charged lepton (i.e. electron or
positron) involved in the scattering process, are combinations of the
weak coupling constants (see, e.g., Cernohorsky 1994).
For the 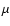 and
and 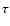 neutrinos and antineutrinos, which are
treated as a single kind of neutrino in our code, we take the
arithmetic mean of the corresponding coupling constants.
For l=0,1 the functions
neutrinos and antineutrinos, which are
treated as a single kind of neutrino in our code, we take the
arithmetic mean of the corresponding coupling constants.
For l=0,1 the functions
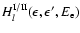 (in units of
(in units of
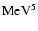 )
are given by Yueh & Buchler (1977 with the
corrections noted by Bruenn 1985).
)
are given by Yueh & Buchler (1977 with the
corrections noted by Bruenn 1985).
Calculating the Legendre coefficients
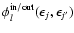 is a computationally
expensive task, since for all combinations
is a computationally
expensive task, since for all combinations
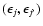 and all radial grid points numerical integrals
over the energy of the charged leptons (Eq. (A.37)) have to be
carried out.
It is, however, sufficient to explicitly compute
and all radial grid points numerical integrals
over the energy of the charged leptons (Eq. (A.37)) have to be
carried out.
It is, however, sufficient to explicitly compute
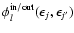 for
for
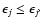 .
The missing coefficients can be obtained by exploiting a number of
symmetry properties (see Cernohorsky 1994).
In doing so, not only the
computational work is reduced by almost a factor of two, but even more
importantly, detailed balance
(
.
The missing coefficients can be obtained by exploiting a number of
symmetry properties (see Cernohorsky 1994).
In doing so, not only the
computational work is reduced by almost a factor of two, but even more
importantly, detailed balance
(
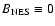 ,
if
,
if
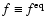 )
can be verified
for the employed approximation and discretization of the
collision integral and its
angular moments to within the roundoff error of the machine, provided
that all integrals over neutrino energies are approximated by simple
zeroth-order quadrature formulae (cf. (Eq. A.22)).
Similarly, one can also verify the conservation of
particle number (Eq. (A.14)) in the corresponding finite
difference representation.
)
can be verified
for the employed approximation and discretization of the
collision integral and its
angular moments to within the roundoff error of the machine, provided
that all integrals over neutrino energies are approximated by simple
zeroth-order quadrature formulae (cf. (Eq. A.22)).
Similarly, one can also verify the conservation of
particle number (Eq. (A.14)) in the corresponding finite
difference representation.
In our neutrino transport code the dependence of the source terms on
the neutrino distribution
and its angular moments is treated fully implicitly in time, i.e. the
time index of the corresponding quantities in
Eqs. (A.10)-(A.12) reads fn+1 and
Ln+1l.
The thermodynamic quantities and the composition of the stellar matter
which are needed to calculate the Legendre coefficients for
inelastic scattering of neutrinos, however, are computed from
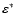 and
and
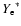 ,
representing the
specific internal energy and electron fraction at the time level after
the hydrodynamic substeps (cf. Sect. 3.6.1).
This allows one to save computer time since the Legendre coefficients
must be computed only once at the beginning of each transport time step.
Comparing to results obtained with a completely time-implicit
implementation of the source terms (i.e. using
,
representing the
specific internal energy and electron fraction at the time level after
the hydrodynamic substeps (cf. Sect. 3.6.1).
This allows one to save computer time since the Legendre coefficients
must be computed only once at the beginning of each transport time step.
Comparing to results obtained with a completely time-implicit
implementation of the source terms (i.e. using
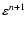 and
and
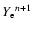 for determining the stellar conditions that enter the
computation of the Legendre coefficients) we have found no
differences in the solutions during the core-collapse phase, where
neutrino-electron scattering plays an important role in redistributing
neutrinos in energy space and thus couples the neutrino transport to the
evolution of the stellar fluid.
for determining the stellar conditions that enter the
computation of the Legendre coefficients) we have found no
differences in the solutions during the core-collapse phase, where
neutrino-electron scattering plays an important role in redistributing
neutrinos in energy space and thus couples the neutrino transport to the
evolution of the stellar fluid.
A.2.5 Neutrino pair production/annihilation by thermal
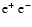 pairs
pairs
Following the suggestion of Pons et al. (1998) we
truncate the Legendre series (A.18)-(A.20) for the
pair-production kernels at
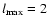 .
The Legendre coefficients are given by (Bruenn 1985; Pons et al. 1998)
.
The Legendre coefficients are given by (Bruenn 1985; Pons et al. 1998)
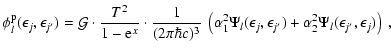 |
|
|
(A.38) |
with
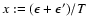 and
and 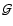 defined by Eq. (A.23).
Explicit expressions for the (dimensionless) functions
defined by Eq. (A.23).
Explicit expressions for the (dimensionless) functions
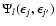 and details about their efficient
calculation are given by Pons et al. (1998).
Also the coefficients
and details about their efficient
calculation are given by Pons et al. (1998).
Also the coefficients
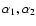 for the different neutrino
flavours can be found there (Pons et al. 1998, Table 1).
for the different neutrino
flavours can be found there (Pons et al. 1998, Table 1).
A.2.6 Nucleon-nucleon bremsstrahlung
Legendre coefficients for the nucleon-nucleon bremsstrahlung process,
assuming nonrelativistic nucleons, are
calculated by using the rates given in Hannestad & Raffelt (1998).
The non-vanishing coefficients read:
with
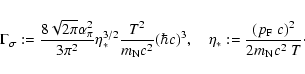 |
(A.41) |
In Eq. (A.40),
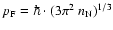 denotes the Fermi momentum for the nucleons,
denotes the Fermi momentum for the nucleons,
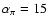 is the
pion-nucleon "fine-structure constant'' (see Hannestad & Raffelt 1998), and
is the
pion-nucleon "fine-structure constant'' (see Hannestad & Raffelt 1998), and
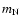 is the nucleon mass.
The analytic form of the dimensionless fit functions g and s(x),
which both depend on the nucleon density
is the nucleon mass.
The analytic form of the dimensionless fit functions g and s(x),
which both depend on the nucleon density 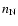 and temperature T of the
stellar medium can be found in Hannestad & Raffelt (1998).
The sum in Eq. (A.39) runs over the individual processes
and temperature T of the
stellar medium can be found in Hannestad & Raffelt (1998).
The sum in Eq. (A.39) runs over the individual processes
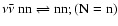 ,
,
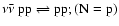 ,
and
,
and
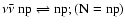 .
The latter process is approximately taken into account by using the
particle density
.
The latter process is approximately taken into account by using the
particle density
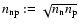 and multiplying the
corresponding contribution to the sum in Eq. (A.39) by
a factor of 28/3 (cf. Thompson et al. 2000).
and multiplying the
corresponding contribution to the sum in Eq. (A.39) by
a factor of 28/3 (cf. Thompson et al. 2000).
The production processes of neutrino-antineutrino pairs both by
the annihilation of
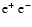 pairs and by the
nucleon-nucleon bremsstrahlung are implemented into the discretized
equations (Eqs. (21), (22), (28),
(29)) by applying the techniques described for the
inelastic scattering reactions (see Sect. A.2.4).
pairs and by the
nucleon-nucleon bremsstrahlung are implemented into the discretized
equations (Eqs. (21), (22), (28),
(29)) by applying the techniques described for the
inelastic scattering reactions (see Sect. A.2.4).


Up: Radiation hydrodynamics with neutrinos
Copyright ESO 2002
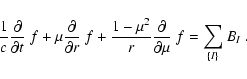
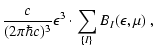
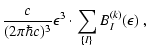
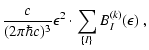
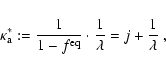
![\begin{displaymath}
B_{\rm AE}(\epsilon,\mu)=
\kappa_{\rm a}^*(\epsilon)[f^{\rm eq}(\epsilon)-f(\epsilon,\mu)]
~.
\end{displaymath}](/articles/aa/full/2002/46/aa2451/img588.gif)
![$\displaystyle B_{\rm S}(\vec{q})=
\int
\frac{{\rm d}^3\vec{\vec{q'}}~}{(2\pi)^3...
...},\vec{q'})
-f_\nu(1-f'_\nu)\widetilde{R}^{\rm out}(\vec{q},\vec{q'})\right]
~,$](/articles/aa/full/2002/46/aa2451/img592.gif)
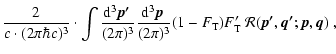
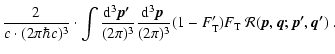
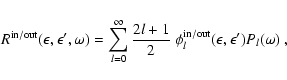
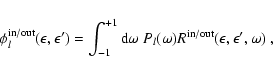
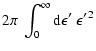
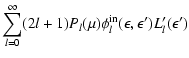
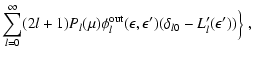
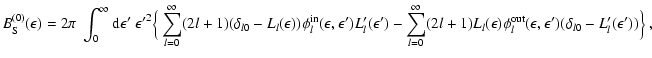
![$\displaystyle B^{(1)}_{\rm S}(\epsilon) =
2\pi~\int_0^\infty {\rm d}\epsilon'~ ...
...on)]
\phi_l^{\rm out}(\epsilon,\epsilon')(\delta_{l0}-L'_l(\epsilon'))\Big\}
~,$](/articles/aa/full/2002/46/aa2451/img627.gif)
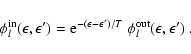
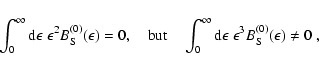
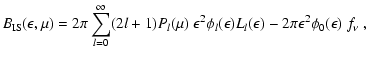
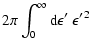
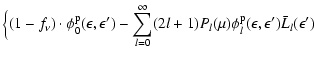
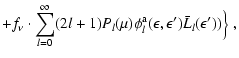
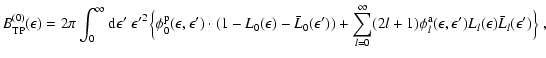
![$\displaystyle B^{(1)}_{\rm TP}(\epsilon) =
2\pi\int_0^\infty {\rm d}\epsilon'~ ...
...n')
[
(l+1)L_{l+1}(\epsilon)+l L_{l-1}(\epsilon)
]\bar{L}_l(\epsilon')
\Big\}~.$](/articles/aa/full/2002/46/aa2451/img642.gif)
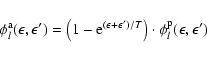
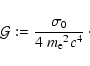
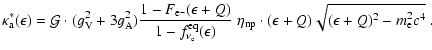
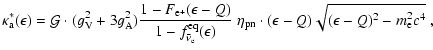
![$\displaystyle 2\int\frac{{\rm d}^3\vec{p}~}{(2\pi\hbar
c)^3}F_{\rm n}(\epsilon)[1-F_{\rm p}(\epsilon)]$](/articles/aa/full/2002/46/aa2451/img665.gif)
![$\displaystyle \frac{n_{\rm p}-n_{\rm n}}{\exp{\left[\psi_{\rm p}-\psi_{\rm n}\right]}-1}
~,$](/articles/aa/full/2002/46/aa2451/img666.gif)
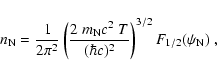
![$\displaystyle \frac{{\cal G}}{8\pi}\cdot
\left\{
\begin{array}{ll}
\eta_{\rm nn...
..._{\rm V}-1)^2+\frac{3}{4}g_{\rm A}^2\right] &({\rm for\ p})~,\end{array}\right.$](/articles/aa/full/2002/46/aa2451/img677.gif)
![$\displaystyle \frac{{\cal G}}{24\pi}\cdot
\left\{
\begin{array}{ll}
\eta_{\rm n...
..._{\rm V}-1)^2-\frac{1}{4}g_{\rm A}^2\right]
&({\rm for\ p})~.\end{array}\right.$](/articles/aa/full/2002/46/aa2451/img679.gif)
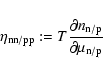
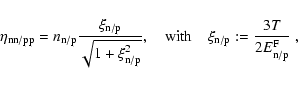
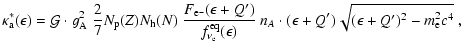
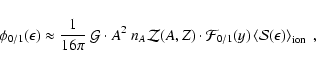
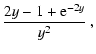
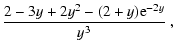
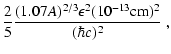
![\begin{displaymath}\mathcal{Z}(A,Z):=
\left[(C_{\rm A}-C_{\rm V})+(2-C_{\rm A}-C_{\rm V})\frac{2Z-A}{A}\right]^2
~\cdot
\end{displaymath}](/articles/aa/full/2002/46/aa2451/img708.gif)