For solving the neutrino radiation hydrodynamics problem we employ the well-known "operator splitting''-approach, a popular method to make large problems computationally tractable by considering them as a combination of smaller subproblems. The coupled set of equations of radiation hydrodynamics (Eqs. (1)-(4), (6)-(8)) is split into a "hydrodynamics part'' and a "neutrino part'', which are solved independently in subsequent ("fractional'') steps. In the "hydrodynamics part'' (Sect. 3.2) a solution of the equations of hydrodynamics including the effects of gravity is computed without taking into account neutrino-matter interactions.
In what we call the "neutrino part'' (Sects. 3.3-3.4) the coupled system of equations
describing the neutrino transport and
the changes of the specific internal energy e and the electron
fraction
![]() of the stellar fluid due to the emission and absorption of
neutrinos are solved. The latter changes are given by the equations
of the stellar fluid due to the emission and absorption of
neutrinos are solved. The latter changes are given by the equations
Within the neutrino part, we calculate in a first step the transport
of energy and
electron-type lepton number by neutrinos and the corresponding
exchange with the stellar fluid
for electron neutrinos (
![]() )
and antineutrinos
(
)
and antineutrinos
(
![]() )
only, which also means that the sum in
Eq. (15) is restricted to
)
only, which also means that the sum in
Eq. (15) is restricted to
![]() .
The
.
The ![]() and
and ![]() neutrinos and their antiparticles, all
represented by a single species ("
neutrinos and their antiparticles, all
represented by a single species ("![]() '') are handled together with
the remaining terms of the sum in Eq. (15) in a second
step.
'') are handled together with
the remaining terms of the sum in Eq. (15) in a second
step.
For the neutrino transport we use the so-called "variable Eddington factor'' method, which determines the neutrino phase-space distribution by iteratively solving the radiation moment equations for neutrino energy and momentum coupled to the Boltzmann transport equation. Closure of the set of moment equations is achieved by a variable Eddington factor calculated from a formal solution of the Boltzmann equation, and the integro-differential character of the latter is tamed by making use of the integral moments of the neutrino distribution as obtained from the moment equations. The method is similar to the one described by Burrows et al. (2000).
For the integration of the equations of hydrodynamics we employ the Newtonian finite-volume hydrodynamics code PROMETHEUS developed by Fryxell et al. (1989). PROMETHEUS is a direct Eulerian, time-explicit implementation of the Piecewise Parabolic Method (PPM) of Colella & Woodward (1984), which is a second-order Godunov scheme employing a Riemann solver. PROMETHEUS is particularly well suited for following discontinuities in the fluid flow like shocks or boundaries between layers of different chemical composition. It is capable of tackling multi-dimensional problems with high computational efficiency and numerical accuracy.
The version of PROMETHEUS used in our radiation hydrodynamics code was provided to us by Keil (1997). It offers an optional generalization of the Newtonian gravitational potential to include general relativistic corrections. The hydrodynamics code was considerably updated and augmented by K. Kifonidis who added a simplified version of the "Consistent Multifluid Advection (CMA)'' method (Plewa & Müller 1999) which ensures an accurate advection of the individual chemical components of the fluid. In order to avoid spurious oscillations arising in multidimensional simulations, when strong shocks are aligned with one of the coordinate lines (the so-called "odd-even decoupling'' phenomenon), a hybrid scheme was implemented (Kifonidis 2000; Plewa & Müller 2001) which, in the vicinity of such shocks, selectively switches from the original PPM method to the more diffusive HLLE solver of Einfeldt (1988).
In what follows we describe the numerical implementation of the
"Newtonian'' limit of the transport equations including
![]() -terms (cf. Sect. 2.2.2).
The general relativistic version of the code is based on almost exactly
the same considerations.
-terms (cf. Sect. 2.2.2).
The general relativistic version of the code is based on almost exactly
the same considerations.
In order to construct a conservative numerical scheme for the system of
moment equations, we integrate the moment equations
(Eqs. (7), (8)) over a zone of
the numerical
![]() -mesh.
-mesh.
After having performed the integral over the volumes ![]() of the radial mesh zones, the moment equations can be rewritten as
evolution equations for the volume-integrated moments (e.g.,
of the radial mesh zones, the moment equations can be rewritten as
evolution equations for the volume-integrated moments (e.g.,
![]() ).
In case of a moving radial grid, where the
volume
).
In case of a moving radial grid, where the
volume ![]() of a grid cell is time dependent, one has to
apply the "moving grid transport theorem'' (see e.g. Müller 1991)
in order to interchange the operators Dt and
of a grid cell is time dependent, one has to
apply the "moving grid transport theorem'' (see e.g. Müller 1991)
in order to interchange the operators Dt and
![]() .
For the special case of a Lagrangian grid,
where the grid moves with the velocity of the stellar fluid, the
latter reads:
.
For the special case of a Lagrangian grid,
where the grid moves with the velocity of the stellar fluid, the
latter reads:
The computational domain
![]() is
covered by Nr radial zones.
As the zone center
is
covered by Nr radial zones.
As the zone center
![]() we define the volume-weighted mean
of the interface coordinates ri and ri+1:
we define the volume-weighted mean
of the interface coordinates ri and ri+1:
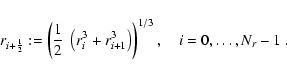 |
(18) |
The spectral range
![]() is covered
by a discrete energy grid consisting of
is covered
by a discrete energy grid consisting of
![]() energy "bins'',
where the centers of these zones are given in terms of the interface values as
energy "bins'',
where the centers of these zones are given in terms of the interface values as
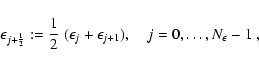 |
(19) |
We employ a time-implicit finite differencing scheme for the moment
equations (Eqs. (7), (8)) in combination with the
equations which describe the exchange of
internal energy and electron fraction with the stellar medium
(Eqs. (15), (16)).
Doing so we avoid the restrictive Courant Friedrichs Lewy (CFL)
condition which explicit numerical schemes have to obey for stability
reasons: for neutrino transport in the optically thin regime the CFL
condition would require
![]() ,
where
,
where
![]() is the size of the smallest zone and
is the size of the smallest zone and ![]() the
numerical time step.
Even more importantly, the time-implicit discretization allows one to
efficiently cope with the different time scales of the problem:
the "stiff'' source terms
introduce a characteristic time scale proportional to the mean free
path
the
numerical time step.
Even more importantly, the time-implicit discretization allows one to
efficiently cope with the different time scales of the problem:
the "stiff'' source terms
introduce a characteristic time scale proportional to the mean free
path ![]() of the neutrinos,
of the neutrinos,
![]() ,
which can be orders of
magnitude smaller than the CFL time step in the
opaque interior of a protoneutron star,
where the optical depth
,
which can be orders of
magnitude smaller than the CFL time step in the
opaque interior of a protoneutron star,
where the optical depth
![]() of individual grid cells becomes
very large.
of individual grid cells becomes
very large.
Applying the procedures described in Sect. 3.3.1 to the moment
equations (Eqs. (7), (8)) we obtain for each
neutrino
species
![]() (the corresponding
index is suppressed in the notation below) the finite
differenced moment equations. On an Eulerian grid they read:
(the corresponding
index is suppressed in the notation below) the finite
differenced moment equations. On an Eulerian grid they read:
Since the radiation moments are defined on a staggered mesh,
the finite-difference equations are second-order accurate in space.
First-order accuracy in time is achieved by employing fully implicit
time-differences ("backward Euler'').
Only the advection terms in the second and forth line of
Eq. (21) and Eq. (22), respectively,
are treated differently (see Sect. 4.3.1 for a motivation):
![\begin{displaymath}\iota(i):=
\left\{
\begin{array}{ll}
i-\frac{1}{2}&\quad {\rm...
...[2mm]
i+\frac{1}{2}&\quad {\rm else}~. \\
\end{array}\right.
\end{displaymath}](/articles/aa/full/2002/46/aa2451/img183.gif) |
(26) |
Using a similar diffusive term in the zeroth moment equation (Eq. (21)) allowed us also to overcome stability problems with the numerical handling of the velocity-dependent terms in the general form of the radiation momentum equation, Eq. (8).
For the solution of the moment equations (Eqs. (7),
(8)), boundary conditions have to be specified at
![]() ,
,
![]() ,
,
![]() and
and
![]() .
In the radial domain the values of quantities at the boundaries
are iteratively obtained from the solution of the Boltzmann
equation (see Sect. 3.4.3 for the boundary conditions
employed there), which has the advantage that in the moment
equations no assumptions have to be made about the angular
distribution of the specific intensity at the
boundaries.
Specifically, at the inner boundary
.
In the radial domain the values of quantities at the boundaries
are iteratively obtained from the solution of the Boltzmann
equation (see Sect. 3.4.3 for the boundary conditions
employed there), which has the advantage that in the moment
equations no assumptions have to be made about the angular
distribution of the specific intensity at the
boundaries.
Specifically, at the inner boundary
![]() is given by
is given by
![]() as computed from the Boltzmann
equation.
To handle the outer boundary, we apply Eq. (22)
on the "half shell'' between
as computed from the Boltzmann
equation.
To handle the outer boundary, we apply Eq. (22)
on the "half shell'' between
![]() and
rNr (Mihalas & Mihalas 1984). Where necessary,
and
rNr (Mihalas & Mihalas 1984). Where necessary,
![]() is
replaced by
is
replaced by
![]() in Eqs. ((21), (22)).
in Eqs. ((21), (22)).
At
![]() the flux in energy space vanishes and hence we simply
set
the flux in energy space vanishes and hence we simply
set
![]() in Eq. (21). At the upper boundary of the spectrum the flux
in energy space,
in Eq. (21). At the upper boundary of the spectrum the flux
in energy space,
![]() is computed by a
(geometrical)
extrapolation of the moments
is computed by a
(geometrical)
extrapolation of the moments
![]() and
and
![]() and by a linear extrapolation of the
advection velocity using
and by a linear extrapolation of the
advection velocity using
![]() and
and
![]() .
Analogous expressions are used for Eq. (22).
.
Analogous expressions are used for Eq. (22).
The finite differenced versions of the operator-splitted source terms
in the energy and lepton number equations (Eqs. (15),
(16)) of the stellar fluid read:
In the finite-differenced version of the (monochromatic) neutrino energy
equation (Eq. (21)) the derivative with respect to energy,
![]() ,
has been written in a conservative form.
When a summation over all energy bins is performed in
Eq. (21), the terms containing
fluxes across the boundaries of the energy zones telescope and an
appropriate finite differenced version of the total
(i.e. spectrally integrated) neutrino energy equation
is recovered.
This essential property does, however, not hold automatically also for
the neutrino number density
,
has been written in a conservative form.
When a summation over all energy bins is performed in
Eq. (21), the terms containing
fluxes across the boundaries of the energy zones telescope and an
appropriate finite differenced version of the total
(i.e. spectrally integrated) neutrino energy equation
is recovered.
This essential property does, however, not hold automatically also for
the neutrino number density
![]() ,
when the naive definition
,
when the naive definition
![]() is adopted. By inserting the latter expression into Eq. (21)
and summing over all energy bins, it can easily be verified that the
corresponding
fluxes across the boundaries of the energy bins do not cancel anymore due
to the finite cell size
is adopted. By inserting the latter expression into Eq. (21)
and summing over all energy bins, it can easily be verified that the
corresponding
fluxes across the boundaries of the energy bins do not cancel anymore due
to the finite cell size
![]() .
.
In order to avoid this problem, we instead derive the moment
equations for ![]() and
and ![]() (by multiplying
Eqs. (7), (8) with
(by multiplying
Eqs. (7), (8) with
![]() )
and
recast them into a conservative form:
)
and
recast them into a conservative form:
With the Eddington factors fH, fK, fL and flow field
![]() being given,
the nonlinear system of equations (Eqs. (21),
(22), (30), (31), (28),
(29)) is solved
for the variables
being given,
the nonlinear system of equations (Eqs. (21),
(22), (30), (31), (28),
(29)) is solved
for the variables
![]() by a Newton-Raphson iteration
(e.g. Press et al. 1992), using the aforementioned boundary conditions.
by a Newton-Raphson iteration
(e.g. Press et al. 1992), using the aforementioned boundary conditions.
This requires the inversion of a block-pentadiagonal
system with 2 Nr+1 rows of blocks. The dimension of an individual
block of the
Jacobian is
![]() in case of the transport of
electron neutrinos and antineutrinos (the number of energy bins
in case of the transport of
electron neutrinos and antineutrinos (the number of energy bins
![]() is multiplied by a factor of two because
is multiplied by a factor of two because
![]() and
and
![]() are treated as separate particles, the other factor of two
comes from the additional transport of neutrino number). In contrast,
muon and tau neutrinos and their antiparticles are considered here as
one neutrino species because their interactions with supernova matter
are roughly the same. In the absence of the corresponding charged
leptons, muon and tau neutrinos are only produced (or annihilated) as
are treated as separate particles, the other factor of two
comes from the additional transport of neutrino number). In contrast,
muon and tau neutrinos and their antiparticles are considered here as
one neutrino species because their interactions with supernova matter
are roughly the same. In the absence of the corresponding charged
leptons, muon and tau neutrinos are only produced (or annihilated) as
![]() pairs and hence do not transport lepton number.
Therefore the blocks have a dimension of
pairs and hence do not transport lepton number.
Therefore the blocks have a dimension of
![]() for these
flavours.
for these
flavours.
For setting up the Jacobian all partial derivatives with respect to the radiation moments can be calculated analytically, whereas the derivatives with respect to electron fraction and specific internal energy are approximated by finite differences.
In order to provide the closure relations (the "variable Eddington
factors'') for the truncated system of moment equations, we have to
solve the Boltzmann equation. Since the emissivity ![]() and the opacity
and the opacity ![]() depend in general also on angular moments
of
depend in general also on angular moments
of ![]() ,
this is actually a nonlinear, integro-differential
problem.
However,
,
this is actually a nonlinear, integro-differential
problem.
However, ![]() and
and ![]() become known functions of only the
coordinates t, r,
become known functions of only the
coordinates t, r, ![]() and
and ![]() ,
when
J and H are used as given solutions of the moment equations.
This allows one to calculate a formal solution of the Boltzmann
equation.
,
when
J and H are used as given solutions of the moment equations.
This allows one to calculate a formal solution of the Boltzmann
equation.
Making the change of variables
(cf. Yorke 1980; Mihalas & Mihalas 1984; Körner 1992; Basheck et al. 1997)
For the moment we shall ignore terms which contain frequency derivatives
![]() (see Eqs. (35), (36)).
These Doppler terms will be included in an operator-split manner.
(see Eqs. (35), (36)).
These Doppler terms will be included in an operator-split manner.
Equations (35), (36) are then discretized on a so-called "tangent ray grid'' (for an illustration, see Fig. 1), the geometry of which being an immediate consequence of the transformation of variables given by Eq. (32). Applying this transformation, partial derivatives of only one momentum-space coordinate s remain, whereas the second coordinate p appears only in a parametric way (cf. Baschek et al. 1997). This greatly facilitates the numerical solution of the system.
A "tangent ray'' k is defined by its "impact parameter'' pk=rk at
![]() .
The coordinate s serves to measure
the path length along the ray.
On each tangent ray k, a staggered numerical mesh is introduced for
the coordinate s.
The zone boundaries (centers) of this mesh are given by
the ray's intersections with the zone boundaries (centers) of the
radial grid (cf. Fig. 1).
With the "flux-like'' variable h being defined at the zone boundaries
sik
and the "density-like'' variable j being defined at the zone centers
.
The coordinate s serves to measure
the path length along the ray.
On each tangent ray k, a staggered numerical mesh is introduced for
the coordinate s.
The zone boundaries (centers) of this mesh are given by
the ray's intersections with the zone boundaries (centers) of the
radial grid (cf. Fig. 1).
With the "flux-like'' variable h being defined at the zone boundaries
sik
and the "density-like'' variable j being defined at the zone centers
![]() ,
the finite-differenced versions of
Eqs. (35), (36) finally can be written down (cf. Mihalas & Klein 1982, Sect. V.2):
,
the finite-differenced versions of
Eqs. (35), (36) finally can be written down (cf. Mihalas & Klein 1982, Sect. V.2):
The frequency derivatives of Eqs. (35), (36),
which were ignored in the finite-difference versions,
Eqs. (39), (40), are
taken into account in a separate step by operator-splitting (the
partially updated values for j and h were marked by asterisks in
Eqs. (39), (40).
The discretization of the corresponding terms is explicit in time and
- provided the acceleration terms in the second line of
Eqs. (35), (36) are neglected -
can be performed straightforwardly using upwind differences in energy
space (
![]() ):
):
![\begin{displaymath}\upsilon_{i_k,k}:=
(1-\mu_{i_k,k}^2)\left[\frac{\beta}{r}\rig...
...i_k,k}^2\left[\frac{\partial\beta}{\partial r}\right]_{i_k}
~,
\end{displaymath}](/articles/aa/full/2002/46/aa2451/img261.gif) |
(44) |
It should be possible to proceed along similar lines for including the exact aberration effects in the Boltzmann solution which, for the time being, includes aberration only in an approximate way on the basis of the replacements given by Eqs. (37), (38). In practice, however, the adopted tangent-ray geometry does not allow for a conservative discretization of the angular derivatives in a way as simple as in the case of the frequency derivatives. We plan to spend extra work on the omitted angular derivatives of the intensity in order to include them in future version of our code.
On the tangent ray grid boundary conditions must be specified for
each ray k at sk,k and at sNr,k.
At the inner core radius (
![]() and
and
![]() )
we set the boundary condition
)
we set the boundary condition
![]() ,
with
,
with
![]() .
For the remaining rays (
.
For the remaining rays (
![]() ), symmetry and
Eq. (34) imply hk,k=0, since
), symmetry and
Eq. (34) imply hk,k=0, since
![]() .
.
At the outer radius
(
![]() and
and
![]() )
we consider Eq. (40) on the "half shell'' between
)
we consider Eq. (40) on the "half shell'' between
![]() and rNr (cf. Sect 3.3.3) and
make the replacement
and rNr (cf. Sect 3.3.3) and
make the replacement
![]() ,
with
,
with
![]() .
.
The physical boundary conditions are described by the functions
![]() and
and
![]() with
with
![]() ,
which specify
the specific intensity entering the computational volume at the
inner and outer surfaces, respectively.
,
which specify
the specific intensity entering the computational volume at the
inner and outer surfaces, respectively.
At the boundaries of the energy grid we use the same type of boundary conditions as described for the moment equations (cf. Sect. 3.3.3).
By virtue of the approximations used to derive the model
equations (Eqs. (35), (36)) and upon
introducing the tangent ray grid,
the system of Eqs. (39), (40) with suitably
chosen boundary conditions can be
solved independently for
each impact parameter pk, each type of neutrino (note that for
simplicity we have dropped the index ![]() in our notation), and - because Doppler shift terms are split off - each
neutrino energy bin
in our notation), and - because Doppler shift terms are split off - each
neutrino energy bin
![]() (index also suppressed).
(index also suppressed).
For the same reasons as detailed in Sect. 3.3,
we have employed fully implicit ("backward Euler'')
time differencing. Solving Eqs. (39),
(40) therefore requires the
separate solution of
![]() (
Nk:=Nr-K0+1 is the number of tangent rays)
pentadiagonal linear systems of dimension
(
Nk:=Nr-K0+1 is the number of tangent rays)
pentadiagonal linear systems of dimension ![]() Nr.
On vector computers, this can be done very
efficiently by employing a vectorization over the index k.
Once the numerical solution for j and h has been obtained,
the monochromatic angular moments and thus the Eddington factors
fH=H/J, fK=K/J and fL=L/J can be computed using the
numerical quadrature formulae
Nr.
On vector computers, this can be done very
efficiently by employing a vectorization over the index k.
Once the numerical solution for j and h has been obtained,
the monochromatic angular moments and thus the Eddington factors
fH=H/J, fK=K/J and fL=L/J can be computed using the
numerical quadrature formulae
Unless the velocity field vanishes identically (in this case
![]() and
and
![]() in Eqs. (39) and
(40), respectively),
an additional complication arises, since the partial derivative
in Eqs. (39) and
(40), respectively),
an additional complication arises, since the partial derivative
![]() has to be
evaluated not only at fixed Lagrangian radius
(the index i in our case)
but also for a fixed value of the angle cosine
has to be
evaluated not only at fixed Lagrangian radius
(the index i in our case)
but also for a fixed value of the angle cosine ![]() .
The angular grid
.
The angular grid
![]() ,
which is associated
with
the radius rin, however, changes as ri moves with time.
As a consequence, e.g., the values of h at the old
time level used in Eq. (40) are
,
which is associated
with
the radius rin, however, changes as ri moves with time.
As a consequence, e.g., the values of h at the old
time level used in Eq. (40) are
![]() and not
and not
![]() ,
the solution
of the previous time step (cf. Mihalas & Mihalas 1984, Sect. 98).
At the beginning of the time step we therefore have to interpolate
the radiation field for each fixed radial index i from
the
,
the solution
of the previous time step (cf. Mihalas & Mihalas 1984, Sect. 98).
At the beginning of the time step we therefore have to interpolate
the radiation field for each fixed radial index i from
the
![]() -grid onto the
-grid onto the
![]() -grid.
If an Eulerian grid is used for the computation,
an additional interpolation in the radial direction is
performed to map from the fixed ri-grid to the coordinates given
by
-grid.
If an Eulerian grid is used for the computation,
an additional interpolation in the radial direction is
performed to map from the fixed ri-grid to the coordinates given
by
![]() (see
Fig. 1).
This seemingly complicated procedure has the advantage of
being computationally much more efficient than directly
discretizing Eqs. (35), (36) in Eulerian
coordinates. In this case the
(see
Fig. 1).
This seemingly complicated procedure has the advantage of
being computationally much more efficient than directly
discretizing Eqs. (35), (36) in Eulerian
coordinates. In this case the
![]() -term, which
originates from making the replacement
-term, which
originates from making the replacement
![]() ,
would
couple grid points of different impact parameters and would therefore
defy an independent treatment of the tangent rays.
,
would
couple grid points of different impact parameters and would therefore
defy an independent treatment of the tangent rays.
A transport time step starts by adopting guess values (e.g., given by the
solution of the previous time step) for J, H,
![]() ,
and e.
The quantities
,
and e.
The quantities
![]() ,
e and the density
,
e and the density ![]() determine the
thermodynamic state and thus the temperature
and chemical potentials. These, together with J and H are used
to evaluate the rhs of the Boltzmann equation.
This allows one to compute its formal
solution and the Eddington factors as detailed in
Sect. 3.4.
The Eddington factors are then fed into the system of moment and
source-term equations, the solution of which (Sect. 3.3)
yields improved values for J, H,
determine the
thermodynamic state and thus the temperature
and chemical potentials. These, together with J and H are used
to evaluate the rhs of the Boltzmann equation.
This allows one to compute its formal
solution and the Eddington factors as detailed in
Sect. 3.4.
The Eddington factors are then fed into the system of moment and
source-term equations, the solution of which (Sect. 3.3)
yields improved values for J, H,
![]() ,
and e. At this point,
where required (e.g., for evaluating
,
and e. At this point,
where required (e.g., for evaluating
![]() ),
the neutrino number density
),
the neutrino number density ![]() and
number flux density
and
number flux density ![]() are conventionally replaced by
are conventionally replaced by
![]() and
and
![]() .
This procedure
is iterated until numerical convergence is achieved.
With the Eddington factors being known from the described
iteration procedure, the complete system of source-term and moment
equations for neutrino energy and number is solved (once) in
order to accomplish lepton number conservation. In this step
.
This procedure
is iterated until numerical convergence is achieved.
With the Eddington factors being known from the described
iteration procedure, the complete system of source-term and moment
equations for neutrino energy and number is solved (once) in
order to accomplish lepton number conservation. In this step
![]() and
and ![]() are treated as additional variables
(cf. Sect. 3.3.5).
are treated as additional variables
(cf. Sect. 3.3.5).
Our experience with the operator-splitting technique has shown that considerable care is necessary in how precisely the equations of hydrodynamics are coupled with the neutrino transport and how the fractional time steps are scheduled. In the following we therefore describe the used procedures in some detail.
Since the hydrodynamics code and the transport solver in general have different requirements for numerical resolution, accuracy and stability, the discretization in both space and time of the two code components is preferably chosen to be independent of each other. In supernova simulations, for example, the time step limit (from the CFL condition) for the hydrodynamic evolution computed by a time-explicit method is typically more restrictive than in the time-implicit treatment of the transport part. Since the transport is computationally much more expensive, one wants to use a larger time step than for the hydrodynamics part. This means that a transport time step is divided into a suitable number of hydrodynamical substeps.
Starting from the hydrodynamic state
![]() at the
old time level tn, the time-explicit PPM algorithm first computes a
solution of the hydrodynamical conservation laws without the
effects of gravity and neutrinos.
From the updated density, the gravitational potential can be
calculated by virtue of Poisson's equation and finally the
gravitational source
terms are applied to the total energy equation (Eq. (3))
and the momentum equation (Eq. (2)).
This completes the "hydrodynamics'' time step with size
at the
old time level tn, the time-explicit PPM algorithm first computes a
solution of the hydrodynamical conservation laws without the
effects of gravity and neutrinos.
From the updated density, the gravitational potential can be
calculated by virtue of Poisson's equation and finally the
gravitational source
terms are applied to the total energy equation (Eq. (3))
and the momentum equation (Eq. (2)).
This completes the "hydrodynamics'' time step with size
![]() ,
which is limited by the CFL-condition (see e.g., LeVeque 1992).
By performing a total of
,
which is limited by the CFL-condition (see e.g., LeVeque 1992).
By performing a total of
![]() substeps
the hydrodynamic state is evolved from the time level tn to the new
time level tn+1 given by
substeps
the hydrodynamic state is evolved from the time level tn to the new
time level tn+1 given by
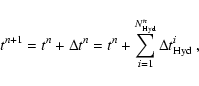 |
(49) |
After the transport time step has been completed, the new neutrino
stress
![]() is used for correcting v* to give the
new velocity vn+1 at time level tn+1:
is used for correcting v* to give the
new velocity vn+1 at time level tn+1:
![\begin{displaymath}[\rho v]^{n+1}=\rho^{n+1} v^{*}+
(Q_{\rm M}^{n+1}- Q_{\rm M}^{n})
\cdot \Delta t^n
~.
\end{displaymath}](/articles/aa/full/2002/46/aa2451/img313.gif) |
(52) |
Radial discretization of the transport and hydrodynamic equations is done on independent grids. Therefore there is freedom to choose the number of zones and their coordinate values separately in both parts of the code. Only quantities which obey conservation laws have to be communicated from the hydro to the transport grid. By invoking the equation of state all other thermodynamical quantities can be derived from the density, the total energy density, momentum density and the number densities of electrons and nuclear species. In the other direction it is the neutrino source terms which have to be mapped back onto the hydro grid.
For the mapping procedure we assume the conserved quantities to be piecewise linear functions of the radius inside the grid cells, with parameters determined by the cell average values and so-called "monotonized slopes'' (for details see, e.g., Ruffert 1992 and references cited therein). In order to achieve global conservation of integral values we then simply average this function within each cell of the target grid of the mapping (cf. Dai & Woodward 1996).
Using this procedure in dynamical supernova simulations, we discovered spurious radial and temporal fluctuations of the temperature, electron fraction, entropy and related quantities inside the opaque protoneutron star unless the hydro and transport grids coincide exactly in this region. The scale of these fluctuations is sensitive to the radial cell size and the size of a time step, the relative amplitude was found to be typically of the order of a few percent, with the exact number varying between different quantities (see Rampp & Janka 2000). These fluctuations are understood from the fact that the mapping of the source terms on the one hand and the internal energy density (resp. temperature) on the other hand implies deviations from local thermodynamical equilibrium between neutrinos and stellar medium. The attempt of the neutrino transport to restore this equilibrium within a given grid cell leads to large net production or absorption rates, driving the temperature in the opposite direction and causing it to perform oscillations in time around a mean value. Despite these oscillations and fluctuations, the use of different numerical grids inside the protoneutron star did not cause noticeable problems for the accuracy of the "global'' evolution of our models, because the conservative mapping describes the exchange of energy and lepton number between neutrinos and the stellar fluid correctly on average.
Being cautious, we take advantage of the option of using different hydro and transport grids only during the early phases of the collapse and in regions of the star, where neutrinos are far from reaching equilibrium with the stellar fluid. In this case no visible fluctuations occur.
The numerical treatment of the radiation hydrodynamics problem should guarantee that the conservation laws for energy and lepton number are fulfilled.
Provided the acceleration terms (
![]() ),
which are of order (v2/c2)and thus usually very small compared to the other terms, are ignored,
the constancy of the total lepton number is ensured by, (a) a
conservative
discretization of the neutrino number equation (Eq. (30)),
(b) a conservative handling of the electron number equation
(Eq. (4)), and (c) the exact numerical balance of the
source terms (cf. Eq. (13))
),
which are of order (v2/c2)and thus usually very small compared to the other terms, are ignored,
the constancy of the total lepton number is ensured by, (a) a
conservative
discretization of the neutrino number equation (Eq. (30)),
(b) a conservative handling of the electron number equation
(Eq. (4)), and (c) the exact numerical balance of the
source terms (cf. Eq. (13))
![]() (defined on the transport grid) and
(defined on the transport grid) and
![]() (defined on the hydro grid).
Point (a) requires that in Eq. (30) the flux divergence is
discretized in analogy to the second line in Eq. (21) and
that the
(defined on the hydro grid).
Point (a) requires that in Eq. (30) the flux divergence is
discretized in analogy to the second line in Eq. (21) and
that the
![]() and
and
![]() terms are combined to
terms are combined to
![]() to be discretized in analogy to the
third line in Eq. (21).
The energy derivative in Eq. (30) is treated in a
conservative way as described in Sect. (3.3.5).
Point (b) is achieved by the use of a conservative numerical
integration of the electron number equation
(Eq. (4)) in the spirit of the PROMETHEUS code, and
requirement (c) is fulfilled by employing a conservative
procedure for mapping the electron
number source term from the transport grid to the hydro grid (see
Sects. 3.6.1, 3.6.2).
Doing so, the total lepton number remains constant in principle at
the level of machine accuracy.
to be discretized in analogy to the
third line in Eq. (21).
The energy derivative in Eq. (30) is treated in a
conservative way as described in Sect. (3.3.5).
Point (b) is achieved by the use of a conservative numerical
integration of the electron number equation
(Eq. (4)) in the spirit of the PROMETHEUS code, and
requirement (c) is fulfilled by employing a conservative
procedure for mapping the electron
number source term from the transport grid to the hydro grid (see
Sects. 3.6.1, 3.6.2).
Doing so, the total lepton number remains constant in principle at
the level of machine accuracy.
Different from the number transport, where the zeroth order moment equation for neutrinos by itself defines a conservation law, the derivation of a conservation law for the total energy implies a combination of the radiation energy and momentum equations. The use of a staggered radial mesh for discretizing the latter equations defies a suitable contraction of terms in analogy to the analytic case. Therefore our numerical description does not conserve neutrino energy with the same accuracy as neutrino number and the quality of total energy conservation has to be verified empirically for a given problem and numerical resolution.
For our supernova simulations, tests showed that neutrino number is
conserved to an accuracy of
better than 10-11 per time step, while for neutrino energy a
value below 10-7 is achieved. With a typical
number of about 50 000 transport time steps for a supernova
simulation we thus find an empirical upper limit for the violation of
energy conservation of ![]() of the neutrino energy.
This translates to
of the neutrino energy.
This translates to ![]() of the internal energy of the
collapsed stellar core, i.e. a few times
of the internal energy of the
collapsed stellar core, i.e. a few times
![]() in
absolute number.
Errors of the same magnitude are introduced by the
non-conservative treatment of the gravitational potential as a source
term in the fluid-energy equation (Eq. (3)).
Note that the use of different grids for the hydrodynamics and the
transport does not affect the energy budget because we employ a
conservative mapping of the neutrino source term between the grids
(see
Sects. 3.6.1, 3.6.2).
in
absolute number.
Errors of the same magnitude are introduced by the
non-conservative treatment of the gravitational potential as a source
term in the fluid-energy equation (Eq. (3)).
Note that the use of different grids for the hydrodynamics and the
transport does not affect the energy budget because we employ a
conservative mapping of the neutrino source term between the grids
(see
Sects. 3.6.1, 3.6.2).
We have not yet coupled our general relativistic version of the neutrino transport to a general relativistic hydrodynamics code. For the time being we work with a basically Newtonian code, which was extended to include post-Newtonian corrections of the gravitational potential. We hope that the deeper gravitational potential can account for the main effects of general relativity on stellar core collapse and the formation of neutron stars which do not approach gravitational instability to become black holes (cf. Bruenn et al. 2001). Because the general relativistic changes of the space-time metric are ignored, a consistent description of the neutrino transport requires that the fully relativistic equations are simplified such that only the effects of gravitational redshift and time dilation are retained.
By comparing the Tolman-Oppenheimer-Volkoff equation for hydrostatic
equilibrium in general relativity (see, e.g., Kippenhahn & Weigert 1990, Sect. 2.6) with its Newtonian counterpart
(cf. Eq. (2)) one can define a modified "gravitational
potential'' which includes correction terms due to pressure and energy
of the stellar medium and the neutrinos:
Equation (53) can be used in the Newtonian hydrodynamic equations (Eqs. (2), (3)) in order to approximately take into account general relativistic effects (cf. Keil 1997). The quality of this approach has to be ascertained empirically by comparison with fully general relativistic calculations. In our case such a comparison yields quite satisfactory results (see Sect. 4.3).
The general relativistic moment equations describing transport of
neutrino energy, momentum and neutrino number can be derived from the
Lindquist-equation (cf. Eq. (5), Sect. 2.2.1).
They are:
In the approximate treatment we neglect the distinction between
coordinate radius and proper radius (
![]() ,
,
![]() )
in Eqs. (54)-(57), and
identify corresponding quantities with their Newtonian counterparts
(
)
in Eqs. (54)-(57), and
identify corresponding quantities with their Newtonian counterparts
(![]() ,
,
![]() ,
,
![]() ).
The same approximations are made in the "parent'' Boltzmann equation
from which the moment equations of the relativistic approximation can
be consistently derived.
Accordingly, the approximations to
Eqs. (54)-(57) contain only general
relativistic redshift and time dilation effects for neutrinos.
Coupling the transport with the Newtonian equations of hydrodynamics,
these restrictions to a fully relativistic treatment
are necessary in order to verify conservation
laws for energy and lepton number of the coupled system.
).
The same approximations are made in the "parent'' Boltzmann equation
from which the moment equations of the relativistic approximation can
be consistently derived.
Accordingly, the approximations to
Eqs. (54)-(57) contain only general
relativistic redshift and time dilation effects for neutrinos.
Coupling the transport with the Newtonian equations of hydrodynamics,
these restrictions to a fully relativistic treatment
are necessary in order to verify conservation
laws for energy and lepton number of the coupled system.
Finite-difference versions of the moment equations and the
corresponding parent Boltzmann equation
for the approximate GR transport are obtained by applying the techniques
described in Sects. 3.3 and 3.4.
The lapse function is calculated by integrating the general
relativistic Euler equation
![]() inward from the surface, where the boundary
condition
inward from the surface, where the boundary
condition
![]() is applied (van Riper 1979).
is applied (van Riper 1979).
Multi-dimensional frequency dependent neutrino transport in moving media and relativistic environments is a challenging problem for future work. Since convective phenomena were recognized to be highly important in supernovae (Herant et al. 1994; Burrows et al. 1995; Janka & Müller 1996; Keil et al. 1996 and refs. therein) one would of course like to perform simulations with Boltzmann neutrino transport also in two and three dimensions. Here we suggest an approximate approach based on a straightforward generalization of our variable Eddington factor method, which offers some advantages concerning computational efficiency. The approximation should be considered as an intermediate step between spherically symmetric and fully multi-dimensional models. Of course, the quality of the approximation for the neutrino transport which we will describe below, will finally have to be checked by a comparison with fully multi-dimensional transport calculations.
Our approximate treatment may be a reasonably accurate and physically justifyable approach for describing neutrino transport in situations where the star does not show a global deformation (e.g., due to rotation) in layers which are opaque to neutrinos, but where inhomogeneities and anisotropies are present only on smaller scales (e.g., due to convection). Multi-dimensional hydrodynamical simulations suggest that convective processes occur in two distinct regions of the supernova core:
Under these circumstances the specific intensity
![]() can be assumed to depend mainly on r but only weakly on longitude
can be assumed to depend mainly on r but only weakly on longitude
![]() and latitude
and latitude ![]() of the background medium.
Hence, like in the spherically
symmetric case, the dependence of the specific intensity on the direction
of propagation
of the background medium.
Hence, like in the spherically
symmetric case, the dependence of the specific intensity on the direction
of propagation ![]() can be described by only one angle
can be described by only one angle
![]() .
The flux is thus approximated as
.
The flux is thus approximated as
![]() and the scalar
and the scalar
![]() is sufficient to define the radiation stress tensor.
is sufficient to define the radiation stress tensor.
In the moment equations,
gradients in the ![]() - and the
- and the ![]() -direction, which describe
the transport of energy and neutrino number into these lateral and
azimuthal directions, are neglected, yet the parametric dependence of
the (scalar) moments on the
coordinates
-direction, which describe
the transport of energy and neutrino number into these lateral and
azimuthal directions, are neglected, yet the parametric dependence of
the (scalar) moments on the
coordinates ![]() and
and ![]() is retained and the radial
transport is computed using the moment equations independently in each
angular zone of the stellar model.
In order to close the set of moment equations, variable Eddington
factors are computed by iterating the Boltzmann equation and
the corresponding moment equations on a
spherically symmetric "image'' of the stellar
background. The latter is defined as the angular average of physical
quantities
is retained and the radial
transport is computed using the moment equations independently in each
angular zone of the stellar model.
In order to close the set of moment equations, variable Eddington
factors are computed by iterating the Boltzmann equation and
the corresponding moment equations on a
spherically symmetric "image'' of the stellar
background. The latter is defined as the angular average of physical
quantities
![]() according to
according to
![]() .
Note that the variable Eddington factors are normalized moments of the
neutrino phase space distribution function and thus should not show
significant
variation with the angular coordinates of the star. This justifies
replacing them by quantities that depend only on the radial position
and time.
.
Note that the variable Eddington factors are normalized moments of the
neutrino phase space distribution function and thus should not show
significant
variation with the angular coordinates of the star. This justifies
replacing them by quantities that depend only on the radial position
and time.
Since for each latitude ![]() and longitude
and longitude ![]() the moment
equations (Eqs. (7), (8)) in our approach are solved
together with the evolution equations of electron fraction and
internal energy due to neutrino sources (Eqs. (15),
(16), local radiative equilibrium can be attained
properly and conservation of energy can be fulfilled.
It is not obvious to us how these fundamental requirements could be
met in a more simple approximation where one uses a
one-dimensional transport scheme to compute the transport on a
spherically symmetric "mean star'', which is obtained at each time
step by averaging the multi-dimensional hydrodynamical stellar model
over angles.
the moment
equations (Eqs. (7), (8)) in our approach are solved
together with the evolution equations of electron fraction and
internal energy due to neutrino sources (Eqs. (15),
(16), local radiative equilibrium can be attained
properly and conservation of energy can be fulfilled.
It is not obvious to us how these fundamental requirements could be
met in a more simple approximation where one uses a
one-dimensional transport scheme to compute the transport on a
spherically symmetric "mean star'', which is obtained at each time
step by averaging the multi-dimensional hydrodynamical stellar model
over angles.
Besides having significant advantages for easy and efficient
implementation on vector and parallel computer architectures, the
suggested approach also saves computer time compared to a multiple
application of a one-dimensional Boltzmann solver.
Let
![]() be the computation time required for
calculating a time step of the full one-dimensional transport problem
and let
be the computation time required for
calculating a time step of the full one-dimensional transport problem
and let
![]() be the number of steps that are
necessary for the iteration between the moment equations and the
Boltzmann equation to achieve convergence.
If
be the number of steps that are
necessary for the iteration between the moment equations and the
Boltzmann equation to achieve convergence.
If
![]() is the total
number of angular zones that discretize the background star, the
computation time for calculating one time step of the
multi-dimensional problem with the described approximate method is
is the total
number of angular zones that discretize the background star, the
computation time for calculating one time step of the
multi-dimensional problem with the described approximate method is
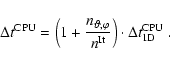 |
(58) |
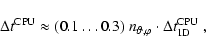 |
(59) |
Copyright ESO 2002