Stationary solutions of the Boltzmann equation of radiative transfer can be calculated analytically, semi-analytically or numerically to high accuracy in a few cases, where a particularly simple form of the emissivity and the opacity is assumed. These problems provide test cases for our new code for solving the equations of neutrino transport. To this end we impose suitably chosen initial and boundary conditions and solve the time-dependent neutrino transport equations numerically, until a stationary state is reached. The numerical solutions can then be compared to the reference solutions. This first class of problems, presented in Sects. 4.1 and 4.2, does neither refer to specific properties of neutrinos nor will the equations of neutrino radiation hydrodynamics, i.e. the coupling of the neutrino transport equation to the equations of hydrodynamics, be tested. Time-dependent hydrodynamical tests will be described in Sect. 4.3.
We first consider the simplest class of radiative transfer problems, namely those where the "background medium'' is assumed to be time-independent and static, i.e. the radial profiles of the emissivity and opacity do not change with time and the velocity and acceleration vanish everywhere and at all times. As usual, the background medium is assumed to be spherically symmetric.
Here, our method for computing the variable Eddington
factor (see Sect. 3.4) by solving the Boltzmann
equation with a finite difference scheme (Mihalas & Klein 1982)
is compared with results obtained from a
general quadrature solution along characteristics (Yorke 1980; Körner 1992; Baschek et al. 1997).
For convenience, we set ![]() in this section.
in this section.
As a test problem we consider a central point source which emits
radiation with an intensity
![]() into a spherical, static and homogeneous
shell of matter bounded by two spheres of radius r0 and R > r0.
The only interaction of the radiation with the medium is by
absorption (
into a spherical, static and homogeneous
shell of matter bounded by two spheres of radius r0 and R > r0.
The only interaction of the radiation with the medium is by
absorption (
![]() ).
The central source is active during the time interval
).
The central source is active during the time interval
![]() .
Initially (t=0), there is no radiation inside the shell.
.
Initially (t=0), there is no radiation inside the shell.
By symmetry, the intensity vanishes for all but the radial
direction of propagation. In the absence of scattering,
it is therefore sufficient to follow the propagation of the light pulse
along a single radial (characteristic) ray. The dependence of
the intensity on the angle can thus conveniently be
suppressed in the notation, writing
| (60) |
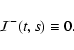 |
(63) |
Figure 2 shows our results for
![]() at the time
t=100, together with the analytical solution (Eq. (63)).
We define the position of the numerically broadened light
front as the radius, where the average of the true
pre and postfront value of the intensity is reached.
In all cases the mean propagation speed is well reproduced, with
some minor loss of accuracy for very large time steps.
The shape of the light front, however, deviates from the true
solution. One observes an artificial precursor together with
a reduced intensity behind the front,
both effects resulting in a spatial broadening of the front.
A clear trend towards larger diffusive broadening with increasing
time steps can be seen from Fig. 2 and
Table 1. This phenomenon was also observed by
Mihalas & Klein (1982), who reported very similar results for their tests.
at the time
t=100, together with the analytical solution (Eq. (63)).
We define the position of the numerically broadened light
front as the radius, where the average of the true
pre and postfront value of the intensity is reached.
In all cases the mean propagation speed is well reproduced, with
some minor loss of accuracy for very large time steps.
The shape of the light front, however, deviates from the true
solution. One observes an artificial precursor together with
a reduced intensity behind the front,
both effects resulting in a spatial broadening of the front.
A clear trend towards larger diffusive broadening with increasing
time steps can be seen from Fig. 2 and
Table 1. This phenomenon was also observed by
Mihalas & Klein (1982), who reported very similar results for their tests.
Table 1 summarizes our results for the width of the front
and compares them to
simulations done with an implementation of the method of characteristics
(Yorke 1980; Körner 1992).
The latter method has the advantage to exactly reproduce the
analytical solution without any smearing of the front, if the
light front is advanced by exactly one grid cell per time step.
Though the ability to reproduce the exact solution appears to be a
very appealing property of the method of characteristics,
the necessary condition
![]() can hardly ever be
accomplished in realistic simulations. This is simply due to the fact
that in typical astrophysical simulations the radial resolution can be
varying over several orders of magnitude, whereas in most
applications the global value of the time step is determined in
some region of the grid.
When doing radiation hydrodynamical simulations, for example, one is usually
interested in resolving time scales different from those
given by the speed of propagating light fronts.
Accordingly, the time steps can be very different from the optimum for
describing the light front propagation.
Our finite difference scheme therefore seems to be preferable to the
method of characteristics as far as the resolution of travelling
discontinuities is concerned (cf. Table 1).
can hardly ever be
accomplished in realistic simulations. This is simply due to the fact
that in typical astrophysical simulations the radial resolution can be
varying over several orders of magnitude, whereas in most
applications the global value of the time step is determined in
some region of the grid.
When doing radiation hydrodynamical simulations, for example, one is usually
interested in resolving time scales different from those
given by the speed of propagating light fronts.
Accordingly, the time steps can be very different from the optimum for
describing the light front propagation.
Our finite difference scheme therefore seems to be preferable to the
method of characteristics as far as the resolution of travelling
discontinuities is concerned (cf. Table 1).
For time steps ![]() significantly smaller than the
radial zone width, a case not discussed by Mihalas & Klein (1982), we
observe some spurious postfront oscillations
(see also Mihalas & Weaver 1982, Sect. 5) .
Their maximum amplitude, however, does not
grow with time, which is in agreement with a local von Neumann
stability analysis for the fully implicit implementation of the equations
(Mihalas & Klein 1982).
If present in practical applications, the oscillations can be damped
by employing an additional diffusive term in Eq. (62),
which is active in nearly transparent regions
(
significantly smaller than the
radial zone width, a case not discussed by Mihalas & Klein (1982), we
observe some spurious postfront oscillations
(see also Mihalas & Weaver 1982, Sect. 5) .
Their maximum amplitude, however, does not
grow with time, which is in agreement with a local von Neumann
stability analysis for the fully implicit implementation of the equations
(Mihalas & Klein 1982).
If present in practical applications, the oscillations can be damped
by employing an additional diffusive term in Eq. (62),
which is active in nearly transparent regions
(
![]() )
of the computational grid
(cf. Sects. 3.3.2, 3.4.2; Blinnikov et al. 1998).
Due to the correspondingly increased diffusivity of the
finite-difference scheme
the light front is smeared over a larger number of zones (
)
of the computational grid
(cf. Sects. 3.3.2, 3.4.2; Blinnikov et al. 1998).
Due to the correspondingly increased diffusivity of the
finite-difference scheme
the light front is smeared over a larger number of zones (
![]() for
for
![]() ;
see also the inserted panel in
Fig. 2a) as compared to the original method
of Mihalas & Klein (1982). Note, however, that the representation of the
front is still better than the results obtained with the method of
characteristics.
;
see also the inserted panel in
Fig. 2a) as compared to the original method
of Mihalas & Klein (1982). Note, however, that the representation of the
front is still better than the results obtained with the method of
characteristics.
| model VAC | model ABS | ||||
|
|
# | ||||
| 0.02 | 5000 | 6 | 25 | 6 | 26 |
| 0.1 | 1000 | 8 | - | 8 | - |
| 0.5 | 200 | 18 | 16 | 16 | 20 |
| 1.0 | 100 | 26 | 1 | 22 | 1 |
| 2.0 | 50 | 37 | 26 | 29 | 26 |
| 10.0 | 10 | 80 | - | 55 | - |
The so-called "homogeneous sphere'' is a test problem frequently employed for radiative transfer calculations (e.g., Bruenn 1985; Schinder & Bludman 1989; Smit et al. 1997). Physically, one can think of a static, homogeneous and isothermal sphere of radius R radiating into vacuum. Inside the sphere, the only interactions of the radiation with the background medium are isotropic absorption and thermal emission of radiation.
Despite of its simplification, the model has some important numerical and physical properties which are typically found in practical applications: Finite difference methods are challenged by the discontinuity at the surface of the sphere. Moreover, the sudden transition from radiation diffusion inside an optically thick sphere to free streaming in the ambient vacuum - a similar but less extreme situation arises in the neutrino-heating region of a core-collapse supernova - is a major source of inaccuracies for approximate radiative transfer methods like, e.g., flux-limited diffusion.
The model is defined by setting
![]() with
with
![]() ,
,
![]() for
for
![]() ,
and
,
and
![]() for r > R.
Since for this choice of parameters, the right hand side of the
Boltzmann equation does not contain terms that depend
explicitly on the angular moments of the radiation field, the solution
of Eq. (6), with
for r > R.
Since for this choice of parameters, the right hand side of the
Boltzmann equation does not contain terms that depend
explicitly on the angular moments of the radiation field, the solution
of Eq. (6), with
![]() ,
can be obtained
analytically by computing a formal solution.
With the boundary conditions
,
can be obtained
analytically by computing a formal solution.
With the boundary conditions
![]() and
and
![]() ,
which account for
isotropy (due to spherical symmetry) of the radiation field at
the center and no incoming radiation at the outer boundary,
respectively, the result for the stationary state
is (see e.g., Smit et al. 1997):
,
which account for
isotropy (due to spherical symmetry) of the radiation field at
the center and no incoming radiation at the outer boundary,
respectively, the result for the stationary state
is (see e.g., Smit et al. 1997):
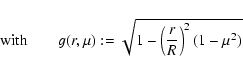 |
(65) |
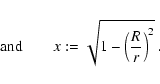
We employ a radial grid consisting of 213 radial zones to cover the range
between r=0 and
![]() .
Approximately 200 zones were distributed logarithmically between
.
Approximately 200 zones were distributed logarithmically between
![]() and
and
![]() ,
about two thirds of which were spent to resolve the sphere.
Initially we set
,
about two thirds of which were spent to resolve the sphere.
Initially we set
![]() everywhere and evolved the
radiation field until a stationary state was reached.
everywhere and evolved the
radiation field until a stationary state was reached.
In Fig. 3 we display the stationary-state solutions for two
models, one with ![]() (Figs. 3a, c) and another with
(Figs. 3a, c) and another with
![]() (Figs. 3b, d), representative of spheres with low
and high optical depth, respectively.
In general, our numerical results agree very well
with the analytical solutions.
The Eddington factor K/J (as calculated from the
Boltzmann equation) and the flux factor H/J (as obtained from the
moment equations) both follow the exact values very
closely (Figs. 3c, d), in case of the flux factor over many
orders of magnitude.
In both models, the transition to
free streaming is reproduced very accurately (Figs. 3c, d).
This region usually causes serious problems for flux-limited
diffusion methods (see e.g., Bruenn 1985; Smit et al. 1997).
Also the forward peaking of the radiation distribution at large
distances from the
surface of the sphere (cf. Eqs. (64), (65)) is
described excellently by our method:
at
(Figs. 3b, d), representative of spheres with low
and high optical depth, respectively.
In general, our numerical results agree very well
with the analytical solutions.
The Eddington factor K/J (as calculated from the
Boltzmann equation) and the flux factor H/J (as obtained from the
moment equations) both follow the exact values very
closely (Figs. 3c, d), in case of the flux factor over many
orders of magnitude.
In both models, the transition to
free streaming is reproduced very accurately (Figs. 3c, d).
This region usually causes serious problems for flux-limited
diffusion methods (see e.g., Bruenn 1985; Smit et al. 1997).
Also the forward peaking of the radiation distribution at large
distances from the
surface of the sphere (cf. Eqs. (64), (65)) is
described excellently by our method:
at
![]() ,
the tangent ray grid
yields approximately 150 angular grid points to resolve the radiation
field from the central source, which has an opening half angle of
only
,
the tangent ray grid
yields approximately 150 angular grid points to resolve the radiation
field from the central source, which has an opening half angle of
only
![]() (
(
![]() ).
These numbers should be compared with calculations employing the
discrete angles (
).
These numbers should be compared with calculations employing the
discrete angles (
![]() )
method: In time dependent neutrino
transport calculations, typically less than 10 angular
grid points can be afforded to equidistantly cover the range
)
method: In time dependent neutrino
transport calculations, typically less than 10 angular
grid points can be afforded to equidistantly cover the range
![]() .
.
Although we have used a geometrical
radial zoning for our tangent-ray grid, we do not find any systematic
effects caused by a "bias'' in angular binning as described by
Burrows et al. (2000).
Far from a central source, they report Eddington factors and flux
factors that asymptote to between 0.96 and 0.98 instead of 1.0 in this
case.
For example, we find values of
K/J=0.996602
for the Eddington factor and
H/J=0.999361 for the flux factor
at
![]() (in the model with
(in the model with ![]() ), to be
compared with
K/J=0.996636 and
H/J=0.998626 obtained from the
analytical solution (Eqs. (64), (4.1)).
), to be
compared with
K/J=0.996636 and
H/J=0.998626 obtained from the
analytical solution (Eqs. (64), (4.1)).
In case of the mean intensity J we observe a systematic trend towards
larger deviations from the true solution for spheres with larger total
optical depth ![]() .
In our "low opacity'' case (
.
In our "low opacity'' case (![]() ,
see Fig. 3a), there
is hardly any difference visible, whereas in the "high opacity'' case
(
,
see Fig. 3a), there
is hardly any difference visible, whereas in the "high opacity'' case
(![]() ,
see Fig. 3b) the numerical solution slightly
overestimates the true solution in a narrow region beneath the surface
of the sphere and underestimates it in the ambient vacuum region. A
detailed analysis of the data yields values of
,
see Fig. 3b) the numerical solution slightly
overestimates the true solution in a narrow region beneath the surface
of the sphere and underestimates it in the ambient vacuum region. A
detailed analysis of the data yields values of ![]() and
and ![]() for
the relative deviations from the analytical solutions in the "low
opacity'' and the "high opacity'' case, respectively.
for
the relative deviations from the analytical solutions in the "low
opacity'' and the "high opacity'' case, respectively.
This finding is caused by the steep opacity gradient near the surface
of the radiating sphere. Since we keep our radial grid to be the same
in all models, the transition from high optical depth
(
![]() ,
if r<R) to transparency
(
,
if r<R) to transparency
(![]() ,
if r>R) occurs in a boundary layer beneath the surface
of the sphere, which is less well resolved when the opacity is very
large.
In the "high opacity''
case, the semi-transparent layer is geometrically much thinner than
in the "low opacity'' case and therefore the radial gradients of the
radiation density are steeper and would require more radial zones for
a proper description.
In fact, in the "low opacity'' case the radial zones of our grid
near the surface of the sphere are optically thin (
,
if r>R) occurs in a boundary layer beneath the surface
of the sphere, which is less well resolved when the opacity is very
large.
In the "high opacity''
case, the semi-transparent layer is geometrically much thinner than
in the "low opacity'' case and therefore the radial gradients of the
radiation density are steeper and would require more radial zones for
a proper description.
In fact, in the "low opacity'' case the radial zones of our grid
near the surface of the sphere are optically thin (
![]() ), whereas in the "high opacity'' case the outermost
zone has already an optical depth of
), whereas in the "high opacity'' case the outermost
zone has already an optical depth of
![]() .
A better quality of the numerical results could be achieved by
increasing the spatial resolution in
the vicinity of large opacity or emissivity gradients and/or by
using higher-order difference schemes.
.
A better quality of the numerical results could be achieved by
increasing the spatial resolution in
the vicinity of large opacity or emissivity gradients and/or by
using higher-order difference schemes.
Due to the absence of scattering in the discussion of the homogeneous sphere problem, the solution of the Boltzmann equation does not require any information from the moment equations. No iteration between both parts of the code is necessary. Therefore this problem allows one to test the algorithm which solves the Boltzmann equation for the radiation intensity independently from the numerical solution of the moment equations. For the stationary state, we find that the radiation moments calculated by a numerical integration of the intensities are consistent with the moments directly obtained from the moment equations to within an accuracy of less than a percent.
Hummer & Rybicki (1971) published stationary-state solutions for the
spherical analogue of the classical Milne problem.
The model comprises a static, spherically symmetric, pure scattering
atmosphere of some radius
![]() ,
with a central point source
that is emitting radiation isotropically with a constant luminosity
L0.
Due to the presence of scattering, the problem is of
integro-differential nature and defies solution by
simply computing the formal solution of the Boltzmann equation.
,
with a central point source
that is emitting radiation isotropically with a constant luminosity
L0.
Due to the presence of scattering, the problem is of
integro-differential nature and defies solution by
simply computing the formal solution of the Boltzmann equation.
The opacity of the atmosphere is assumed to be solely caused by isotropic
scattering with a simple power-law dependence on radius:
For a number of atmospheres defined by various combinations of the
parameters
![]() ,
,
![]() and
and
![]() ,
Hummer & Rybicki (1971) computed numerically the zeroth moment J
and the Eddington factor K/J of the stationary-state solution as a
function of radius.
They found values of better than one percent for the accuracy of their
results.
The stationary-state solution for the first moment H as a function
of radius can easily be derived analytically from the zeroth order
moment equation (Eq. (7), with
,
Hummer & Rybicki (1971) computed numerically the zeroth moment J
and the Eddington factor K/J of the stationary-state solution as a
function of radius.
They found values of better than one percent for the accuracy of their
results.
The stationary-state solution for the first moment H as a function
of radius can easily be derived analytically from the zeroth order
moment equation (Eq. (7), with
![]() ):
):
The idealized concept of a central point source with a given luminosity
L0 is in practice modeled by imposing a suitable inner boundary
condition at some finite radius
![]() ,
which bounds the
atmosphere from below.
Since all atmospheres with a scattering opacity according to
Eq. (66) become optically thick at sufficiently small
radius, it is reasonable to employ the diffusion ansatz
,
which bounds the
atmosphere from below.
Since all atmospheres with a scattering opacity according to
Eq. (66) become optically thick at sufficiently small
radius, it is reasonable to employ the diffusion ansatz
We evolved the transport to stationary-state solutions for the two
sets of parameter combinations
(n=1.5,
![]() ,
,
![]() ),
and (n=2,
),
and (n=2,
![]() ,
,
![]() ).
The total optical depth at
).
The total optical depth at
![]() is larger than
55 for all models of the former class (n=1.5) and larger than
90 for all of
the models with n=2. Hence, we verify that the inner boundary is
placed at
a radius which is sufficiently small to justify the use of the
diffusion approximation (Eq. (68)) for the inner boundary
condition.
In order to test the sensitivity of the results to the corresponding angular dependence of the
intensity (Eq. (68)), we have calculated a model
with a different angular dependence:
is larger than
55 for all models of the former class (n=1.5) and larger than
90 for all of
the models with n=2. Hence, we verify that the inner boundary is
placed at
a radius which is sufficiently small to justify the use of the
diffusion approximation (Eq. (68)) for the inner boundary
condition.
In order to test the sensitivity of the results to the corresponding angular dependence of the
intensity (Eq. (68)), we have calculated a model
with a different angular dependence:
![]() .
The parameter
.
The parameter
![]() is chosen such that
is chosen such that
![]() .
This prescription is appropriate for an
atmosphere around a central hollow sphere with radius
.
This prescription is appropriate for an
atmosphere around a central hollow sphere with radius
![]() ,
which is irradiated from below by the central point source.
Figure 4d shows the Eddington factor of the stationary
state for this model.
The numerical solution deviates visibly from the reference solution
only in the innermost radial zones.
,
which is irradiated from below by the central point source.
Figure 4d shows the Eddington factor of the stationary
state for this model.
The numerical solution deviates visibly from the reference solution
only in the innermost radial zones.
![\begin{figure}
\includegraphics[width=12.5cm,clip]{2451f4.eps}\end{figure}](/articles/aa/full/2002/46/aa2451/Timg456.gif) |
Figure 4:
Stationary state solutions for selected radiation
quantities as a function of radius obtained
with our radiative transfer code (solid lines). Our results are
compared with the reference solutions (crosses) and asymptotic
solutions (dashed lines) of Hummer & Rybicki (1971).
Panel a): mean intensity J (times r2) for the combination
of model parameters
|
In the models with n=1.5 the standard radial grid consisted of 200 logarithmically distributed zones with some additional zones giving higher resolution near the surface of the atmosphere, whereas 250 equidistant radial zones were used for the models with n=2. Additional tests with 500 radial grid points were performed for some selected models without finding significant changes. Figure 4 shows some results of our tests together with the data of Hummer & Rybicki (1971). The agreement is excellent. In all models we were able to reproduce the analytical solution for the flux (Eq. (67)) with a relative accuracy of at least 10-4 throughout the atmosphere.
![\begin{figure}
\includegraphics[width=12.5cm,clip]{2451f5.eps}\end{figure}](/articles/aa/full/2002/46/aa2451/Timg457.gif) |
Figure 5:
Metric functions |
Schinder & Bludman (1989) considered the effects of a strong gravitational field
in some of the radiative transfer problems discussed above, in
particular in the cases of a homogeneous sphere and a static
scattering atmosphere.
They computed stationary-state solutions numerically for the
general relativistic equations of radiative transfer and compared the
results to the weak field limit.
For a static background (
![]() ),
and by application of a change of coordinates
),
and by application of a change of coordinates
![]() ,
Schinder & Bludman (1989) simplified the general relativistic moment equations
(Eqs. (54), (55)) to
,
Schinder & Bludman (1989) simplified the general relativistic moment equations
(Eqs. (54), (55)) to
Different from the moment equations, which we treat in their most general form (Eqs. (54), (55)), our implementation of the tangent ray scheme for computing the variable Eddington factors employs a number of approximations. In particular, by using straight lines for the tangent rays, general relativistic ray bending is not included. The current tests therefore serve the purpose of clarifying the influence of these approximations on the quality of the solutions of the moment equations. Schinder & Bludman (1989) found significant differences of the Eddington factors for the general relativistic and Newtonian simulations of the scattering atmosphere (while in case of the homogeneous sphere the differences were minor). The scattering atmospheres therefore seems to be an ideal test case for our purposes.
Following Schinder & Bludman (1989),
we choose the parameters
![]() and
n=2. The variation of the metric functions
and
n=2. The variation of the metric functions
![]() and
and
![]() with radius is depicted in Fig. 5a.
All other model parameters like boundary conditions and initial
conditions are the same as in the "weak-field''-case which is defined
by
with radius is depicted in Fig. 5a.
All other model parameters like boundary conditions and initial
conditions are the same as in the "weak-field''-case which is defined
by
![]() (see above).
The stationary-state Eddington factor as computed from the Boltzmann
equation in our program is displayed as a function of
radius in Fig. 5c. The deviation from the
relativistically correct results of Schinder & Bludman (1989) is significant.
On the other hand, our result is very close to the corresponding
"weak-field'' case, which is not shown in Fig. 5.
This indicates that general relativistic ray bending, which is not
correctly taken into account in our calculation, has a determining
influence on the Eddington factor, while
the contraction of rods and time dilation - both included in our
calculation of the Eddington factor - are of minor importance.
Indeed, the relativistically correct characteristic curves
deviate considerably from straight rays, as can be seen
in Schinder & Bludman (1989, Fig. 9).
(see above).
The stationary-state Eddington factor as computed from the Boltzmann
equation in our program is displayed as a function of
radius in Fig. 5c. The deviation from the
relativistically correct results of Schinder & Bludman (1989) is significant.
On the other hand, our result is very close to the corresponding
"weak-field'' case, which is not shown in Fig. 5.
This indicates that general relativistic ray bending, which is not
correctly taken into account in our calculation, has a determining
influence on the Eddington factor, while
the contraction of rods and time dilation - both included in our
calculation of the Eddington factor - are of minor importance.
Indeed, the relativistically correct characteristic curves
deviate considerably from straight rays, as can be seen
in Schinder & Bludman (1989, Fig. 9).
The analytical stationary-state solution for the radiation flux density,
which is easily verified![]() to read
to read
![]() ,
(with
,
(with
![]() ), is reproduced with an
accuracy of 10-7.
This, of course, was to be expected for the atmosphere with
isoenergetic scattering,
since in the stationary state, the solution H(r) is
solely determined by the zeroth moment equation (Eq. (69))
with no reference to the (incorrect) Eddington factor.
), is reproduced with an
accuracy of 10-7.
This, of course, was to be expected for the atmosphere with
isoenergetic scattering,
since in the stationary state, the solution H(r) is
solely determined by the zeroth moment equation (Eq. (69))
with no reference to the (incorrect) Eddington factor.
More remarkably, the quality of our solution for
the mean intensity J(r), which is governed in the stationary
state by Eq. (70) and thus
is directly influenced by the Eddington factor, appears to be rather
good, too.
As can be seen from Fig. 5b,
the slope of the general relativistic result is reproduced correctly
throughout the atmosphere.
The quantitative agreement is quite satisfactory as well.
In judging the accuracy of our results one has to keep in mind that
the model computed here is a rather extreme case in two respects:
Firstly, the deviations of the metric functions
![]() and
and
![]() from unity (see Fig. 5a) are larger
than those typically encountered in supernova simulations when the
neutron star is not going to collapse to a black hole.
Secondly, as stated in the beginning, the effect of a curved spacetime
on the radiation field was observed by Schinder & Bludman (1989) to be much
larger for the scattering atmosphere than in a case dominated by
absorption (and emission). We expect real situations to be somewhere
in between these two extremes.
from unity (see Fig. 5a) are larger
than those typically encountered in supernova simulations when the
neutron star is not going to collapse to a black hole.
Secondly, as stated in the beginning, the effect of a curved spacetime
on the radiation field was observed by Schinder & Bludman (1989) to be much
larger for the scattering atmosphere than in a case dominated by
absorption (and emission). We expect real situations to be somewhere
in between these two extremes.
![\begin{figure}
\includegraphics[width=12.5cm,clip]{2451f6.eps} \end{figure}](/articles/aa/full/2002/46/aa2451/Timg471.gif) |
Figure 6:
Stationary-state angular mean J (times
r2) of the intensity as measured in the comoving frame of
reference. The abscissa gives the radial position. Results are
shown for gray scattering
atmospheres that expand according to a linear (Model "LVL'';
Panel a) and the quadratic (Model "QVL'';
Panel b) velocity law.
The thin vertical line marks the upper boundary of the atmospheres.
Different line styles of the curves correspond to different values
of the parameter
|
In the following section we consider radiative transfer problems in moving,
yet stationary background media. This means that in addition to
time-independent radial profiles of the opacity and emissivity,
a time-independent velocity field as a function of radius is prescribed.
Stationary-state solutions for the radiation field are expected to
exist is such cases and have been computed to high accuracy for
some test problems including differentially moving atmospheres with
relativistic velocities.
By comparison with fully (special) relativistic calculations, we are not
only able to
test our implementation of the velocity dependent terms but can also
judge the quality of the employed
![]() -approximation of
special relativistic effects in the equations of radiative transfer.
-approximation of
special relativistic effects in the equations of radiative transfer.
Upon introducing a non-vanishing velocity field a particular frame has
to be specified, where physical quantities are measured. In all cases
considered in this work, the latter is chosen to be the Lagrangian or
comoving frame of reference. This has to be distinguished from
the (numerical) coordinate grid that is used to simply label the
events in spacetime. Although the
transformation between different coordinate grids is trivial from an
analytical point of view (e.g., the simple replacement
![]() transforms from Eulerian
to Lagrangian coordinates), the numerical
treatment can be involved (cf. Sect. 3.4, where our
algorithm for computing a formal solution of the radiative transfer
equation in Eulerian coordinates is described).
Therefore we present test results obtained with two different
versions of our radiative-transfer code, one which uses
Lagrangian coordinates and another one which employs an Eulerian
coordinate grid.
transforms from Eulerian
to Lagrangian coordinates), the numerical
treatment can be involved (cf. Sect. 3.4, where our
algorithm for computing a formal solution of the radiative transfer
equation in Eulerian coordinates is described).
Therefore we present test results obtained with two different
versions of our radiative-transfer code, one which uses
Lagrangian coordinates and another one which employs an Eulerian
coordinate grid.
![\begin{figure}
\includegraphics[width=12.5cm,clip]{2451f7.eps}\end{figure}](/articles/aa/full/2002/46/aa2451/Timg473.gif) |
Figure 7:
Frequency integrated zeroth order angular moment of the
comoving frame
intensity (
|
Mihalas (1980) presents stationary-state solutions for the same type of purely scattering atmospheres considered above. In addition to the static case, he investigated differentially expanding atmospheres with relativistic velocities.
We refer to this paper and study two classes of atmospheres as test
problems, which differ in the functional dependence of the expansion
velocity (
![]() )
on the radius:
)
on the radius:
The scattering opacity of the expanding atmospheres is the same
as the one used for the static cases in
Sect. 4.1 except for the unit of length, which,
for the ease of comparison, is adopted from Mihalas (1980):
For our simulations we used a numerical grid with 200 radial
points, which were initially distributed logarithmically between
![]() and
and
![]() .
Following Mihalas (1980) as closely as possible,
we impose the boundary conditions
.
Following Mihalas (1980) as closely as possible,
we impose the boundary conditions
| = | |||
| = | (73) |
We compare our stationary-state solutions with results obtained by
Mihalas (1980). In the latter investigation a numerical method that is
accurate to all orders in v/c was
employed to solve the stationary radiative transfer equation.
We therefore do not only test the correct numerical implementation of
the
![]() equations (Eqs. (6)-(8)),
but we can also get a feeling for the quality of the
equations (Eqs. (6)-(8)),
but we can also get a feeling for the quality of the
![]() -approximation to the special relativistic transfer
equation.
All characteristic features
of the solution, discussed in detail by Mihalas (1980), are reproduced
correctly by our implementation of the
-approximation to the special relativistic transfer
equation.
All characteristic features
of the solution, discussed in detail by Mihalas (1980), are reproduced
correctly by our implementation of the
![]() equations.
It is remarkable how accurately the fully relativistic solutions are
reproduced (Fig. 6). The differences are
equations.
It is remarkable how accurately the fully relativistic solutions are
reproduced (Fig. 6). The differences are ![]() 10%,
even for
10%,
even for
![]() .
.
![\begin{figure}
\includegraphics[width=12.5cm,clip]{2451f8.eps}\end{figure}](/articles/aa/full/2002/46/aa2451/Timg495.gif) |
Figure 8:
Spectral distributions of the angular moment J of the
comoving frame intensity for our
stationary-state solutions of the
|
Mihalas (1980) computed stationary-state solutions also for relativistically expanding nongray atmospheres, i.e., the opacity and emissivity depended explicitly on the radiation frequency. Therefore the full frequency dependence of the comoving frame Boltzmann equation had to be retained. The atmospheres were assumed to be stationary, to emit a thermal continuum of radiation, and to be isothermal, i.e., no radial or temporal variations of the source function were present. The radiation-matter interaction was solely via absorption and emission.
Introducing the dimensionless "frequency''
![]() (the
temperature T is measured in units of the Boltzmann constant
(the
temperature T is measured in units of the Boltzmann constant
![]() ),
the emissivity reads
),
the emissivity reads
Following Mihalas (1980),
we consider the two examples (1) ![]() ,
,
![]() ,
and (2)
,
and (2)
![]() ,
,
![]() .
In the former case the frequency
.
In the former case the frequency ![]() ,
where the opacity jump is located, is considerably larger than the
frequency of the maximum of the Planck function
(
,
where the opacity jump is located, is considerably larger than the
frequency of the maximum of the Planck function
(
![]() ),
whereas it is close to the maximum in the latter case.
),
whereas it is close to the maximum in the latter case.
The radial extent of the atmospheres was chosen to be
![]() in both cases. For all models the linear
law (m=1, cf. Eq. (71)) for the expansion
velocity as a function of radius was used.
The results presented below were obtained using an Eulerian
coordinate grid. Our code version with a Lagrangian grid yields very
similar results.
in both cases. For all models the linear
law (m=1, cf. Eq. (71)) for the expansion
velocity as a function of radius was used.
The results presented below were obtained using an Eulerian
coordinate grid. Our code version with a Lagrangian grid yields very
similar results.
We have used 200 logarithmically distributed radial zones for the
radial range
![]() ,
supplemented by a few additional
zones between
,
supplemented by a few additional
zones between
![]() .
Boundary conditions were chosen as usual: Spherical symmetry at the
coordinate center requires
.
Boundary conditions were chosen as usual: Spherical symmetry at the
coordinate center requires
![]() ,
and demanding that no
radiation is entering through the surface of the atmosphere translates to
the condition
,
and demanding that no
radiation is entering through the surface of the atmosphere translates to
the condition
![]() .
.
The energy grid consisted of 21 bins (very similar results were
obtained using 8 and 12 bins instead) of equal width covering the
range
![]() for Model (1) and
for Model (1) and
![]() for Model (2), respectively.
Details about the stationary-state solutions
and their physical interpretation can be found in Mihalas (1980, Sect. 5).
In our test calculations we were able to reproduce all qualitative
trends discussed there.
The quantitative agreement of the zeroth order angular moment J of the
specific intensity is within a few percent
(see Fig. 7),
even for the case of
for Model (2), respectively.
Details about the stationary-state solutions
and their physical interpretation can be found in Mihalas (1980, Sect. 5).
In our test calculations we were able to reproduce all qualitative
trends discussed there.
The quantitative agreement of the zeroth order angular moment J of the
specific intensity is within a few percent
(see Fig. 7),
even for the case of
![]() .
This, as previously stated, does not only demonstrate the accuracy of
our numerical implementation
but even more importantly also justifies the physical
approximations employed in the underlying finite difference equations.
Note that in applications of our code to supernova calculations, one
expects velocities that are not in excess of
.
This, as previously stated, does not only demonstrate the accuracy of
our numerical implementation
but even more importantly also justifies the physical
approximations employed in the underlying finite difference equations.
Note that in applications of our code to supernova calculations, one
expects velocities that are not in excess of
![]() .
.
A rigorous comparison of the spectral distribution of the
angular moment J as calculated by our radiative transfer code
(cf. Fig. 8) with the results of Mihalas (1980) is
difficult, since he shows only results for the
static case and the rather extreme case
![]() .
The latter atmosphere obviously cannot be modeled reasonably well
with our
.
The latter atmosphere obviously cannot be modeled reasonably well
with our
![]() -code.
Nevertheless, by inspection of Figs. 3 and 4 of Mihalas (1980) one can
infer that the shapes of our spectra as displayed in
Fig. 8 exhibit the correct qualitative dependence on the
expansion velocity.
-code.
Nevertheless, by inspection of Figs. 3 and 4 of Mihalas (1980) one can
infer that the shapes of our spectra as displayed in
Fig. 8 exhibit the correct qualitative dependence on the
expansion velocity.
As an important consistency check we verified that, to order
![]() ,
the numerical solution of our implementation of the
comoving frame equations shows the correct transformation properties of
the stress-energy tensor of radiation (see Eq. (10))
and no unphysical artifacts are caused by the choice of a moving
reference frame (cf. the critique of Lowrie et al. 1999).
,
the numerical solution of our implementation of the
comoving frame equations shows the correct transformation properties of
the stress-energy tensor of radiation (see Eq. (10))
and no unphysical artifacts are caused by the choice of a moving
reference frame (cf. the critique of Lowrie et al. 1999).
For this purpose results are produced for neutrino transport in a
thermally and hydrodynamically frozen post-bounce model of
a supernova calculation by Bruenn (1993). This model can be characterized
as follows:
Neutrinos are emitted from a hot and dense hydrostatic inner core with
a radius of
![]() km.
This inner core is surrounded by a supersonically infalling outer core,
which is effectively transparent to the radiation.
Velocities in this outer atmosphere range from
km.
This inner core is surrounded by a supersonically infalling outer core,
which is effectively transparent to the radiation.
Velocities in this outer atmosphere range from
![]() to
to
![]() .
.
The stress-energy tensor as derived from the stationary-state solution of the comoving frame transport equation (Eq. (6)) is transformed to the Eulerian frame (i.e. the inertial frame in which the center of the star is at rest) and can then be compared with the result of an independent calculation which solves the transport equation directly in the Eulerian frame.
Figure 9 shows the components
![]() and
and
![]() of the
stress-energy tensor (scaled by r2 c and r2, respectively).
Due to the large inwardly
directed velocities in the outer atmosphere, the neutrinos emitted by
the inner core are blueshifted for observers which
are locally comoving with the fluid flow (see the bold
lines in Fig. 9).
When the stress-energy tensor is transformed to the
Eulerian frame (Eq. (10)), this effect obviously
disappears (thin lines in Fig. 9).
Comparison with the stress-energy tensor obtained by solving the
transport equation directly in the Eulerian frame
(dashed lines in Fig. 9) reveals good agreement for both
the energy density E and the energy
flux density F in the rapidly moving atmosphere. This demonstrates
that no unphysical frame dependence is present in the calculations.
The fluctuations of the transformed energy flux density near the
center are caused by the term
of the
stress-energy tensor (scaled by r2 c and r2, respectively).
Due to the large inwardly
directed velocities in the outer atmosphere, the neutrinos emitted by
the inner core are blueshifted for observers which
are locally comoving with the fluid flow (see the bold
lines in Fig. 9).
When the stress-energy tensor is transformed to the
Eulerian frame (Eq. (10)), this effect obviously
disappears (thin lines in Fig. 9).
Comparison with the stress-energy tensor obtained by solving the
transport equation directly in the Eulerian frame
(dashed lines in Fig. 9) reveals good agreement for both
the energy density E and the energy
flux density F in the rapidly moving atmosphere. This demonstrates
that no unphysical frame dependence is present in the calculations.
The fluctuations of the transformed energy flux density near the
center are caused by the term
![]() in the expression for
in the expression for
![]() in Eq. (10). Because J (and K)
are large compared with H in the dense interior, even small
velocities lead to a significant "advective contribution'' to
in Eq. (10). Because J (and K)
are large compared with H in the dense interior, even small
velocities lead to a significant "advective contribution'' to
![]() .
.
Note that an Eulerian-frame calculation in general requires complicated velocity-dependent transformations of the source terms on the rhs of the transport equation (see Mihalas & Mihalas 1984). This, however, is unnecessary in the specific situation of the discussed model: Because the region where most of the neutrinos are produced moves with low velocities, the source terms there can be evaluated in the rest frame of the fluid. In the outer atmosphere on the other hand, where the large velocities would require a careful transformation, the source terms nearly vanish. This allowed us to simply drop the velocity-dependent terms on the lhs of Eq. (6) in order to perform a calculation with results that are in agreement with the Eulerian frame solution in the low-density part of the star.
Our new neutrino hydrodynamics code has already been applied to
dynamical supernova simulations (Rampp & Janka 2000).
Here we report some results of a Newtonian calculation of the
collapse phase of a stellar iron core with mass
![]() (plus the innermost
(plus the innermost
![]() of the silicon shell).
It is the core of a
of the silicon shell).
It is the core of a
![]() progenitor
star (Model "s15s7b2'', Woosley 1999; Heger 2000).
We compare the results to a calculation published by Bruenn & Mezzacappa (1997).
The input physics, in particular the stellar model and the
high-density equation of state, were adopted from
model "B'' of Bruenn & Mezzacappa (1997), with the exception that we do
not include neutrinos other than
progenitor
star (Model "s15s7b2'', Woosley 1999; Heger 2000).
We compare the results to a calculation published by Bruenn & Mezzacappa (1997).
The input physics, in particular the stellar model and the
high-density equation of state, were adopted from
model "B'' of Bruenn & Mezzacappa (1997), with the exception that we do
not include neutrinos other than
![]() .
This,
however, does not make a difference during the collapse phase where the
electron degeneracy is so high that only
.
This,
however, does not make a difference during the collapse phase where the
electron degeneracy is so high that only
![]() can be produced in
significant numbers.
can be produced in
significant numbers.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{2451f10.eps}\end{figure}](/articles/aa/full/2002/46/aa2451/Timg528.gif) |
Figure 10:
Profiles of the total lepton fraction
|
The hydrodynamics was solved on a grid with 400 radial zones out to 20 000 km, which were moved with the infalling matter during core collapse. For the transport we used an Eulerian grid with 213 geometrically spaced radial zones, 233 tangent rays and 21 energy bins geometrically distributed between 0 and 380 MeV the center of the first zone being at 2 MeV.
![\begin{figure}
\includegraphics[width=10cm,clip]{2451f11.ps}\end{figure}](/articles/aa/full/2002/46/aa2451/Timg529.gif) |
Figure 11:
Central lepton fraction
|
The total lepton fraction
![]() and the entropy per baryon at the center of the core as a function of
the central density are displayed in Fig. 11.
The agreement with results of Bruenn & Mezzacappa (1997) is excellent.
Also the total lepton fraction as a function of enclosed mass matches
perfectly (Fig. 10).
Defining the shock formation point according to Bruenn & Mezzacappa (1997) as
the mass coordinate where the entropy per baryon after
core bounce first reaches a value of
and the entropy per baryon at the center of the core as a function of
the central density are displayed in Fig. 11.
The agreement with results of Bruenn & Mezzacappa (1997) is excellent.
Also the total lepton fraction as a function of enclosed mass matches
perfectly (Fig. 10).
Defining the shock formation point according to Bruenn & Mezzacappa (1997) as
the mass coordinate where the entropy per baryon after
core bounce first reaches a value of
![]() we find
we find
![]() .
This is about
.
This is about
![]() or 5%
larger than the value given by Bruenn & Mezzacappa (1997, Table V).
or 5%
larger than the value given by Bruenn & Mezzacappa (1997, Table V).
Judging our results, one should, of course, take into account
that Bruenn & Mezzacappa (1997) employed
a multi-group flux-limited diffusion (MGFLD) approximation for treating
the neutrino transport, whereas our code solves the Boltzmann equation.
Mezzacappa & Bruenn (1993b,c) performed a detailed comparison of
core-collapse simulations with MGFLD and with their Boltzmann solver
based on the
![]() -method.
For the quantities presented here they also found good agreement of
their results throughout the inner core.
-method.
For the quantities presented here they also found good agreement of
their results throughout the inner core.
In the outer regions of the collapsing core, the situation is somewhat
different:
Mezzacappa & Bruenn (1993b,c) demonstrated that a
number of quantities reveal significant deviations between
MGFLD and the Boltzmann transport (
![]() -method).
In particular, they obtained an electron neutrino
fraction which was by up to 20% larger in the Boltzmann run.
For the total lepton fraction, however, the difference was only 1%.
Our results (Fig. 10) confirm the agreement of Boltzmann and
MGFLD results for the latter quantity.
A more detailed comparison between the variable
Eddington factor method and the
-method).
In particular, they obtained an electron neutrino
fraction which was by up to 20% larger in the Boltzmann run.
For the total lepton fraction, however, the difference was only 1%.
Our results (Fig. 10) confirm the agreement of Boltzmann and
MGFLD results for the latter quantity.
A more detailed comparison between the variable
Eddington factor method and the
![]() -method,
however, is desirable and currently underway.
-method,
however, is desirable and currently underway.
![\begin{figure}
\includegraphics[width=12.5cm,clip]{2451f12.eps}\end{figure}](/articles/aa/full/2002/46/aa2451/Timg535.gif) |
Figure 12:
Electron neutrino fraction
|
A few quantities exhibit spurious oscillations as a function of the
radial (mass-) coordinate and time in our core-collapse simulations.
Figure 12a shows such features for
the electron neutrino fraction in the mass shells
![]() when the central density is
when the central density is
![]()
![]() .
Similar structures are visible in the profile of the entropy per
baryon and in the neutrino luminosity as a function of radius (or
mass) once the central density becomes larger than
.
Similar structures are visible in the profile of the entropy per
baryon and in the neutrino luminosity as a function of radius (or
mass) once the central density becomes larger than
![]()
![]() .
They can also be seen in the
central entropy as a function of the central density or time
(cf. Fig. 11b).
Mezzacappa & Bruenn (1993c) found a similar effect in their
core-collapse calculations. They identified the finite
spectral resolution of the degenerate Fermi distribution of the
electron neutrinos
to be the origin of these oscillations (Mezzacappa & Bruenn 1993c, Sect. 3.3).
.
They can also be seen in the
central entropy as a function of the central density or time
(cf. Fig. 11b).
Mezzacappa & Bruenn (1993c) found a similar effect in their
core-collapse calculations. They identified the finite
spectral resolution of the degenerate Fermi distribution of the
electron neutrinos
to be the origin of these oscillations (Mezzacappa & Bruenn 1993c, Sect. 3.3).
For comparison, we have computed a collapse model with a significantly improved spectral resolution: instead of 21 bins we used 81 energy zones to describe the energy spectrum between 0 and 380 MeV. A result of this simulation is displayed in Fig. 12b. The neutrino fraction (and related quantities) are now perfectly smooth functions of the mass coordinate.
A reasonable compromise between accuracy and computational load could be achieved by using approximately 20-30 (geometrically spaced) energy bins. This seems to be sufficient to adequately treat the sharp Fermi surface of the degenerate distribution of electron neutrinos that builds up during collapse. Even for less energy bins fluctuating quantities follow the correct evolutionary trends (Fig. 12a). Therefore we conclude with the remark that the presence of oscillations in some transport quantities may be considered as undesirable. The overall evolution of the collapsing core, its deleptonization or the shock formation radius, however, were found not to be sensitive to such "noise''.
Also during the post-bounce evolution (for which the transport of
![]() was included), we determined no significant differences
between the dynamical evolution of a model with 17 energy bins and
a model computed with 27 energy bins, using an otherwise identical
setup: At a
time of 100 ms after bounce, the structure of the models, measured by
the radial positions of fluid elements with the same mass coordinate,
agreed within a relative error of <1%.
This is corroborated by the fact that
for given snapshots from the dynamical evolution we found the neutrino
source terms
was included), we determined no significant differences
between the dynamical evolution of a model with 17 energy bins and
a model computed with 27 energy bins, using an otherwise identical
setup: At a
time of 100 ms after bounce, the structure of the models, measured by
the radial positions of fluid elements with the same mass coordinate,
agreed within a relative error of <1%.
This is corroborated by the fact that
for given snapshots from the dynamical evolution we found the neutrino
source terms
![]() and also
and also ![]() to be practically identical
in both calculations.
to be practically identical
in both calculations.
Varying the number of radial zones for the hydrodynamic and transport
parts of the code between 100 and 200 and using a comoving
hydrodynamic grid during the phase of stellar core collapse, we found
no significant changes of the results. The same holds true for the
post-bounce evolution where we switch to a fixed, Eulerian grid.
The only exception to this insensitivity is the central density at
bounce, which shows variations of up to ![]() ,
depending on the size
of the innermost zones of the hydrodynamic grid.
,
depending on the size
of the innermost zones of the hydrodynamic grid.
The choice of the radial grid, however, also influences the size of the numerical time step. According to our experience the latter has to be chosen very carefully. We give two examples here:
We also tried to assess the quality of our approximate treatment of
general
relativity (GR) in the equations of hydrodynamics and neutrino transport
(cf. Sect. 3.7).
For this purpose we performed core-collapse
simulations for the
![]() progenitor star "s15s7b2'' and
compared characteristic quantities with the information given for a MGFLD
simulation of the same star in a recent paper by Bruenn et al. (2001), and
for a Boltzmann simulation by Liebendörfer et al. (2001a).
progenitor star "s15s7b2'' and
compared characteristic quantities with the information given for a MGFLD
simulation of the same star in a recent paper by Bruenn et al. (2001), and
for a Boltzmann simulation by Liebendörfer et al. (2001a).
For the hydrodynamics we used 400 radial zones out to 10 000 km, which were moved with the infalling matter during core collapse. The transport was solved on an Eulerian grid with 200 geometrically spaced radial zones, 220 tangent rays and 17 energy bins geometrically distributed between 0 and 380 MeV the center of the first zone being at 2 MeV.
At bounce, which occurs at
![]() (
(
![]() )
after the start of the calculation, the central density reaches a
maximum of
)
after the start of the calculation, the central density reaches a
maximum of
![]()
![]() (
(
![]()
![]() )
in our GR
model (for comparison, the corresponding values for the Newtonian runs
are given in brackets). The hydrodynamic shock forms at a mass
coordinate of
)
in our GR
model (for comparison, the corresponding values for the Newtonian runs
are given in brackets). The hydrodynamic shock forms at a mass
coordinate of
![]() (
(
![]() ).
For the same stellar model, Bruenn et al. (2001) found a bounce density of
).
For the same stellar model, Bruenn et al. (2001) found a bounce density of
![]()
![]() for the general
relativistic simulation
(
for the general
relativistic simulation
(
![]()
![]() ).
The corresponding time of the bounce was
).
The corresponding time of the bounce was
![]() (
(
![]() ).
Liebendörfer et al. (2001a) located the shock formation at a mass coordinate of
).
Liebendörfer et al. (2001a) located the shock formation at a mass coordinate of
![]() (
(
![]() ).
).
Since the collapse time is determined by the slow initial phase of the
contraction, which is sensitive to the
initial conditions and the details of the numerical treatment at the
start of the calculation (Liebendörfer, personal communication),
it may be better to use the difference between the GR and the
Newtonian simulations, instead of comparing absolute times at bounce.
Our value of
![]() is very
close to the result of Bruenn et al. (2001):
is very
close to the result of Bruenn et al. (2001):
![]() .
A part of the remaining difference may be attributed to the fact
that Bruenn et al. (2001) employed a MGFLD
approximation of the neutrino transport with some smaller
differences also in the input physics (e.g., Bruenn et al. 2001 as
well as Liebendörfer et al. 2001a did not take into account ion-ion correlations for the
coherent scattering, but we did).
.
A part of the remaining difference may be attributed to the fact
that Bruenn et al. (2001) employed a MGFLD
approximation of the neutrino transport with some smaller
differences also in the input physics (e.g., Bruenn et al. 2001 as
well as Liebendörfer et al. 2001a did not take into account ion-ion correlations for the
coherent scattering, but we did).
At the level of comparison which is possible on grounds of published numbers we conclude that the agreement between our approximate treatment of GR and the relativistic core collapse seems to be reasonably good.
Copyright ESO 2002