![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2642f1.eps}
\end{figure}](/articles/aa/full/2002/43/aa2642/Timg34.gif) |
Figure 1: Cartoon of the basic structure caused by the interaction of the expanding ejecta with the HII-region. |
We consider grains that are collisionally heated in the shocked circumstellar plasma downstream of the blast wave.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2642f1.eps}
\end{figure}](/articles/aa/full/2002/43/aa2642/Timg34.gif) |
Figure 1: Cartoon of the basic structure caused by the interaction of the expanding ejecta with the HII-region. |
The structure caused by the interaction of the expanding ejecta with
its CSM is visualised in Fig. 1.
The shocked circumstellar gas is compressed to a thin layer
that grows approximately as
![]() (Chevalier 1982), where
(Chevalier 1982), where
![]() is the assumed constant speed of the blast wave and t the time since
the shock reached the HII-region. Downstream it is bounded by the contact discontinuity
to the shocked outer parts of the expanding ejecta. This ejected material is heated
by both the reverse shock and by a shock reflected from the inner boundary of the
HII-region (Borkowski et al. 1997). It is thought
to be the origin of the strong emission in Ly
is the assumed constant speed of the blast wave and t the time since
the shock reached the HII-region. Downstream it is bounded by the contact discontinuity
to the shocked outer parts of the expanding ejecta. This ejected material is heated
by both the reverse shock and by a shock reflected from the inner boundary of the
HII-region (Borkowski et al. 1997). It is thought
to be the origin of the strong emission in Ly![]() and H
and H![]() at a distance of
at a distance of
![]() 0.6 of the radius of the thick inner ring (Michael et al. 1998),
that was measured by the HST close to the time of
the ISOCAM observations.
We do not expect strong MIR emission from
the shocked ejected material for the following reasons:
0.6 of the radius of the thick inner ring (Michael et al. 1998),
that was measured by the HST close to the time of
the ISOCAM observations.
We do not expect strong MIR emission from
the shocked ejected material for the following reasons:
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{ms2642f2.eps}\hspace*{4mm}\includegraphics[width=6.7cm,clip]{ms2642f3.eps}
\end{figure}](/articles/aa/full/2002/43/aa2642/Timg42.gif) |
Figure 2:
Temperature distributions of spherical silicate and graphite grains for various
grain sizes in the shocked CSM,
assuming a density of the shocked gas of
|
The collisional heating of a grain in a hot plasma depends mainly on the temperatures
of electrons and ions and the number density of the different species of the gas![]() .
We fix these properties to be
broadly consistent with the observed radio and X-ray emission from the CSM. An analysis of
the X-ray observations made with the ROSAT satellite towards SN 1987A up to and including
the epoch of the ISOCAM observations is given in Appendix A.
For temperatures above
.
We fix these properties to be
broadly consistent with the observed radio and X-ray emission from the CSM. An analysis of
the X-ray observations made with the ROSAT satellite towards SN 1987A up to and including
the epoch of the ISOCAM observations is given in Appendix A.
For temperatures above ![]()
![]() ,
as encountered
in the shocked gas, the grain heating of the smaller grains principally contributing
to the emission observed by ISOCAM is mainly determined by the plasma density (see e.g. Dwek &
Arendt 1992). As the physical conditions are somewhat uncertain we will consider two cases
(models I and II) with different temperatures and densities.
The parameters of models I and II are summarised in
Table 1 and will be justified in the following.
,
as encountered
in the shocked gas, the grain heating of the smaller grains principally contributing
to the emission observed by ISOCAM is mainly determined by the plasma density (see e.g. Dwek &
Arendt 1992). As the physical conditions are somewhat uncertain we will consider two cases
(models I and II) with different temperatures and densities.
The parameters of models I and II are summarised in
Table 1 and will be justified in the following.
| model I | model II | |
|
shock velocity |
4100 km s-1 | 2900 km s-1 |
| electron temperature
|
|
|
| ion temperature
|
|
|
| hydrogen density
|
|
|
| helium density
|
|
|
| metallicity Z |
|
|
Borkowski et al. (1997) have shown that an assumption of constant density, as suggested by
Chevalier & Dwarkadas, can explain the soft X-ray emission (Hasinger et al. 1996) until
at least 3000 days after outburst. They derived a pre-shock hydrogen density of
![]() with a
corresponding shock speed
with a
corresponding shock speed ![]() of the blast wave of
of the blast wave of
![]() .
In their calculations the HII-region was modelled as a thick torus in which
the inner ring seen by the HST is embedded. They also mentioned that for a different structure of the HII-region
higher densities would be possible. Indeed, a shock speed of
.
In their calculations the HII-region was modelled as a thick torus in which
the inner ring seen by the HST is embedded. They also mentioned that for a different structure of the HII-region
higher densities would be possible. Indeed, a shock speed of
![]() as derived from radio
observations (Gaensler et al. 1997) would require a hydrogen density of the HII-region of
about
as derived from radio
observations (Gaensler et al. 1997) would require a hydrogen density of the HII-region of
about
![]() .
It might also be possible, that the density increased with time
(see Appendix A) although the X-ray
measurements are also consistent with a constant external density.
.
It might also be possible, that the density increased with time
(see Appendix A) although the X-ray
measurements are also consistent with a constant external density.
For simplicity we assume that at the time of the ISOCAM observations
the blast wave was still expanding into a homogeneous HII-region. We will
consider hydrogen densities of
![]() (model I) and
(model I) and
![]() (model II) for the
pre-shock region.
The density of the gas is assumed to be compressed by a factor of four downstream of the blast wave and
to stay constant in the whole interaction zone.
(model II) for the
pre-shock region.
The density of the gas is assumed to be compressed by a factor of four downstream of the blast wave and
to stay constant in the whole interaction zone.
In converting the densities given by Borkowski et al. into hydrogen number density and ionic abundances needed for the calculation of dust heating (Sect. 2.2) we adopted the abundances of the thick inner ring given by Lundqvist & Fransson (1996). On this basis we took helium to be a factor of 2.5 more abundant than in the sun, and approximated the metallicity of all heavier elements to be 0.3 solar.
Because of the long equipartition time of the shocked circumstellar plasma the electron temperature should be much lower than the temperature for the ions and should increase with the distance to the outer shock (see e.g. Burrows et al. 2000). Thus, in calculating the grain heating we use two different temperatures for electrons and ions. As for the density, the temperature of the shocked CSM is taken to be independent of position.
The ion temperature ![]() is taken to be (see e.g. Longair 1997)
is taken to be (see e.g. Longair 1997)
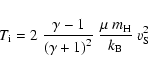 |
(1) |
For the electrons we choose a temperature close to those derived from X-ray observations and
predicted by numerical calculations appropriate to SN 1987A.
From X-ray observations made with the ROSAT-satellite Hasinger et al. (1996)
derived a temperature of approximately
![]() .
Analysing the X-ray spectrum of SN 1987A, taken later with CHANDRA,
using a shock model with a constant
.
Analysing the X-ray spectrum of SN 1987A, taken later with CHANDRA,
using a shock model with a constant ![]() ,
a higher electron temperature of the
order of
,
a higher electron temperature of the
order of ![]()
![]() was found
(Burrows et al. 2000; Park et al. 2002). In our calculation we will adopt
was found
(Burrows et al. 2000; Park et al. 2002). In our calculation we will adopt
![]() K.
K.
The dust in the CSM is taken to be spherical for simplicity as there is no observational evidence for other grain shapes in the CSM of SN 1987A. Spherical grains are also generally assumed in the literature for grains produced in stellar winds (e.g. Gail & Sedlmayr 1999). However, if the grains are not too different from being spherical this assumption should not influence significantly our results about the properties of the grains in the CSM. For example, it has been found, that the temperature of spheroidal grains heated by the interstellar radiation field (ISRF) can only vary by more than 10% if the axial ratio exceeds a value of 2 (Voshchinnikov et al. 1999).
The grains are heated by collisions with electrons and ions of the hot ionized shocked plasma.
The gas species is assumed to transfer all
(if it sticks) or only a part (if it is not stopped) of the kinetic energy into thermal
energy of the grain. The calculation of the energy deposition of
non-stopping particles is based on their stopping-distances (ranges) in
solids![]() .
For the heating by ions we considered in addition to
hydrogen and helium also the next most abundant elements oxygen, nitrogen and carbon.
The emission from larger grains we derived from their equilibrium temperatures.
For smaller grains, where the deposited
energy is typically larger than the thermal energy, we took their temperature fluctuations into account.
The model for stochastic dust emission from a hot plasma
is described in more detail in Popescu et al. (2000).
As typical dust species we consider graphite and silicate grains.
The temperature distributions of very small silicate and graphite grains in model I
are shown in Fig. 2 where it can be seen, that small grains
can be heated to very high temperatures. The smallest grains with 10 Å radius
will reach temperatures well above their evaporation temperature.
The grains contributing to the measured IR emission should therefore not be smaller than this size.
.
For the heating by ions we considered in addition to
hydrogen and helium also the next most abundant elements oxygen, nitrogen and carbon.
The emission from larger grains we derived from their equilibrium temperatures.
For smaller grains, where the deposited
energy is typically larger than the thermal energy, we took their temperature fluctuations into account.
The model for stochastic dust emission from a hot plasma
is described in more detail in Popescu et al. (2000).
As typical dust species we consider graphite and silicate grains.
The temperature distributions of very small silicate and graphite grains in model I
are shown in Fig. 2 where it can be seen, that small grains
can be heated to very high temperatures. The smallest grains with 10 Å radius
will reach temperatures well above their evaporation temperature.
The grains contributing to the measured IR emission should therefore not be smaller than this size.
Because iron is expected to form in cool stellar outflows independent of the C/O ratio and
is potentially one of the main condensates in the circumstellar environment of oxygen rich stars
(see e.g. Gail & Sedlmayr 1999, and references there),
we also carried out calculations for pure iron grains.
For electrons in iron grains
we used the analytical expression for the electron range in graphite derived by Dwek
& Smith (1996) on basis of observational data, correcting for the different
density. The optical properties
of iron spheres we derived using MIE-theory (Bohren & Huffman 1983), whereby we
included the dependence of the dielectric function
in the IR on size and temperature of the iron grains (Fischera 2000).
For the heat capacity of iron grains cooler than 298 K
we used values tabulated in the American Institute of Physics Handbook (1972).
For iron grains warmer than this we used an analytical expression for the heat capacity given
by Chase (1998), assuming that iron is in the ![]() -
-![]() -phase.
-phase.
The variation of the equilibrium temperature of spherical
silicate, graphite, and iron grains in the shocked CSM is shown
in Fig. 3. The different behaviour of the three species
allows some information about dust composition to be derived from the ISOCAM
measurements.
Grain temperatures for the case
![]() are also given.
As seen in the figure the grain
temperature of small silicate and graphite grains
is nearly insensitive to
are also given.
As seen in the figure the grain
temperature of small silicate and graphite grains
is nearly insensitive to ![]() since the electrons are not stopped by the grains. The equilibrium temperatures
are consistent with the colour temperatures
since the electrons are not stopped by the grains. The equilibrium temperatures
are consistent with the colour temperatures ![]() we derived in
Paper I for a modified Planck spectrum
we derived in
Paper I for a modified Planck spectrum
![]() ,
where
,
where
![]() is the Planck function, ranging from
is the Planck function, ranging from ![]() 200 K (
200 K (![]() )
to
)
to ![]() 290 K (
290 K (![]() ). Because of stronger heating due to the higher grain
density and the weaker cooling due to lower emissivities in comparison to
silicate and graphite grains pure iron grains attain the highest
temperatures. We also note that for the conditions in the shocked CSM,
graphite grains are hotter than silicate grains. In less dense plasmas (e.g.
). Because of stronger heating due to the higher grain
density and the weaker cooling due to lower emissivities in comparison to
silicate and graphite grains pure iron grains attain the highest
temperatures. We also note that for the conditions in the shocked CSM,
graphite grains are hotter than silicate grains. In less dense plasmas (e.g.
![]() )
one would expect a slightly
higher temperature for silicate grains (Dwek 1987; Fischera 2000).
)
one would expect a slightly
higher temperature for silicate grains (Dwek 1987; Fischera 2000).
The temperature of small spherical iron grains depends strongly on grain size. This was also noted by Chlewicki & Laureijs (1988) for iron grains heated by the interstellar radiation field.
In order to construct a SED for comparison with the data a functional form
for the grain size distribution must be adopted.
The size distribution of the grains in the shocked circumstellar environment of SN 1987A
is not known and might be modified in comparison to the initial distribution in the CSM
by different processes like evaporation during the UV-flash or sputtering in the
shocked gas as will be shown later.
However, for simplicity we assume, that the grains
in the shocked CSM have a grain size distribution similar to grains
in the ISM of our galaxy and can be described by
a simple power law
![]() with power index kand a minimum and a maximum grain size
with power index kand a minimum and a maximum grain size
![]() and
and ![]() .
Following Biermann & Harwit (1980)
a power law distribution should be
a general description of a grain size distribution resulting
from grain-grain collisions and would especially describe
the grain size distribution in the atmospheres of red-giants.
In contrast to the emission from grains in the ISM, heated by the ISRF,
where only stochastically heated small grains
can achieve high enough temperatures to emit at shorter wavelengths
(Draine & Anderson 1985),
in the shocked CSM of SN 1987A larger grains can also contribute to the measured fluxes.
The composite SEDs are relatively insensitive to
.
Following Biermann & Harwit (1980)
a power law distribution should be
a general description of a grain size distribution resulting
from grain-grain collisions and would especially describe
the grain size distribution in the atmospheres of red-giants.
In contrast to the emission from grains in the ISM, heated by the ISRF,
where only stochastically heated small grains
can achieve high enough temperatures to emit at shorter wavelengths
(Draine & Anderson 1985),
in the shocked CSM of SN 1987A larger grains can also contribute to the measured fluxes.
The composite SEDs are relatively insensitive to
![]() ,
which we fixed at
10 Å.
,
which we fixed at
10 Å.
For each of models I and model II for the shocked gas we made calculations taking various combinations of the following parameters as free variables:
Copyright ESO 2002