

Up: Infrared emission towards SN 1987A
3 Results
The results of the model calculations are summarised in Table 2, where we give
for each fit also the reduced
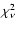 ,
where
,
where 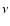 is the number of free parameters.
The best fits obtained for the two mixtures are shown in Fig. 4 together
with the fitted spectrum for silicate grains.
The emission spectrum is such that
measurements at longer wavelengths (e.g. Lundqvist et al. 1999)
are too insensitive to probe the emission from this region.
The fits can be summarised as follows:
is the number of free parameters.
The best fits obtained for the two mixtures are shown in Fig. 4 together
with the fitted spectrum for silicate grains.
The emission spectrum is such that
measurements at longer wavelengths (e.g. Lundqvist et al. 1999)
are too insensitive to probe the emission from this region.
The fits can be summarised as follows:
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{ms2642f5.eps}\hspace*{4mm}\includegraphics[width=6.7cm,clip]{ms2642f6.eps}
\end{figure}](/articles/aa/full/2002/43/aa2642/Timg90.gif) |
Figure 4:
Theoretical emission spectra of dust in the shocked circumstellar medium of SN 1987A for model I
(
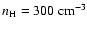 )
and model II ( )
and model II (
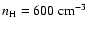 ).
Shown are spectra from pure silicate (dotted line) and the best fits with a
mixture of silicate with graphite (dashed line) and with a mixture of silicate with
iron (solid line). The grains are assumed to have a grain size distribution ).
Shown are spectra from pure silicate (dotted line) and the best fits with a
mixture of silicate with graphite (dashed line) and with a mixture of silicate with
iron (solid line). The grains are assumed to have a grain size distribution
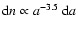 with minimum and maximum grain radii of 10 Å and
with minimum and maximum grain radii of 10 Å and
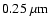 .
The ISOCAM fluxes (triangles), shown with the widths of the
filters as horizontal lines, have been colour corrected
to the spectrum of the silicate-iron mixture. The shown uncertainties are the
absolute uncertainties in the integrated flux densities (taken from Table 2 of
Paper I)
which are .
The ISOCAM fluxes (triangles), shown with the widths of the
filters as horizontal lines, have been colour corrected
to the spectrum of the silicate-iron mixture. The shown uncertainties are the
absolute uncertainties in the integrated flux densities (taken from Table 2 of
Paper I)
which are 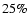 (
(
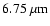 ), ), 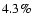 (
(
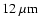 )
and
5.5% ( )
and
5.5% (
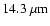 ). These uncertainties are a combination of the systematic
calibration uncertainties, which dominates at 12 and 14.3 ). These uncertainties are a combination of the systematic
calibration uncertainties, which dominates at 12 and 14.3
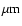 ,
and the
random uncertainties. ,
and the
random uncertainties.
|
- 1.
- Fit parameter:
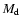 .
.
We simply compared the measured flux densities in the IR with the theoretical emission spectra
of three different grain
compositions (pure silicate, graphite or iron) with fixed grain size distribution for
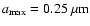 and k=3.5 as proposed for the grains in the ISM (MRN, 1977).
and k=3.5 as proposed for the grains in the ISM (MRN, 1977).
For both model I and model II a better fit is achieved under the assumption
of pure graphite grains instead of silicate grains in the circumstellar environment.
As seen in Fig. 4 the flux at
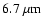 is too high to be emitted from silicate grains.
Because of the high predicted temperatures a pure iron composition is even more unlikely.
is too high to be emitted from silicate grains.
Because of the high predicted temperatures a pure iron composition is even more unlikely.
- 2.
- Fit parameter: k,
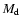 .
.
For each of pure silicate, graphite and iron we varied the power k of the size distribution with
fixed
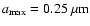 .
.
The derived grain size distributions for graphite grains in model I
and for silicate grains in both models are consistent with k=3.5.
For graphite grains in model II, which reach too high temperatures, a flatter distribution (k<2.25)
is required.
No grain size distribution could be found which admitted a pure iron solution.
- 3.
- Fit parameter: Dust mixture,
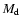 .
.
For a fixed grain size distribution with power k=3.5 and
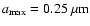 we varied the composition
of circumstellar grains, for a mixture of silicate with iron grains and a mixture
of silicate with graphite grains.
we varied the composition
of circumstellar grains, for a mixture of silicate with iron grains and a mixture
of silicate with graphite grains.
Excellent fits could be achieved for silicate-iron mixture in model I and for the silicate-graphite
mixture in model II (see also Fig. 4).
- 4.
- Fit parameter:
 ,
,
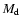 .
.
For a given dust composition (silicate, graphite and the two derived mixtures)
and a fixed size distribution with power k=3.5 we varied
 .
.
The maximum grain sizes in model I are significantly smaller than
in model II. In model I for
silicate, graphite or the silicate-graphite mixture a better fit can be
achieved with
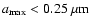 .
The estimated maximum grain sizes of all
considered compositions
in model II are several times larger.
We also examined a pure iron composition
and found that the maximum grain size would be unrealistically large
with
.
The estimated maximum grain sizes of all
considered compositions
in model II are several times larger.
We also examined a pure iron composition
and found that the maximum grain size would be unrealistically large
with
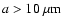 .
.
Due to the large number of free parameters several solutions
with different compositions and grain size distributions are possible.
The derived values like
 ,
k or the mixture of the composition
are interrelated and depend on the plasma density.
Despite these uncertainties the following conclusions could be
reached largely independent of the assumptions:
,
k or the mixture of the composition
are interrelated and depend on the plasma density.
Despite these uncertainties the following conclusions could be
reached largely independent of the assumptions:
- 1.
- Luminosity
For the luminosity of the collisionally heated dust 11 years after outburst we obtained
(dependent on composition and the assumed plasma density)
values for 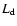 in the range
in the range
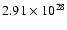 to
to
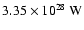 .
This can be compared with the crude estimate
of
.
This can be compared with the crude estimate
of
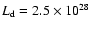 W given in Paper I where we
approximated the dust emission spectrum with a simple modified black body spectrum.
As already mentioned in Paper I the luminosity in the MIR
is larger than in X-rays. Despite the increase of the X-ray luminosity since detection
W given in Paper I where we
approximated the dust emission spectrum with a simple modified black body spectrum.
As already mentioned in Paper I the luminosity in the MIR
is larger than in X-rays. Despite the increase of the X-ray luminosity since detection  1400 days after outburst (Hasinger et al. 1996) the luminosity in the energy range
0.5 to 10 keV even
1400 days after outburst (Hasinger et al. 1996) the luminosity in the energy range
0.5 to 10 keV even  13 years
after outburst was only
13 years
after outburst was only
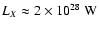 (Burrows et al. 2000).
(Burrows et al. 2000).
- 2.
- Composition
The dust is most likely a mixture of silicate with
iron or silicate with graphite. Also pure graphite gives a reasonable fit.
Pure silicate on the other hand seems to be unlikely and pure iron can be excluded.
- 3.
- Dust-to-gas ratio
Considering only cases where  is not larger than
is not larger than
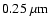 the dust mass is found to be nearly independent of
composition and grain size distribution.
The corresponding acceptable fits for model I (
the dust mass is found to be nearly independent of
composition and grain size distribution.
The corresponding acceptable fits for model I (
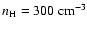 )
yield dust masses
in the range
)
yield dust masses
in the range
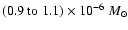 and those for
model II (
and those for
model II (
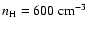 )
yield dust masses in the range
)
yield dust masses in the range
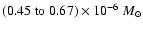 .
.
Taking these values the dust-to-gas ratio is only mildly dependent
on gas density as one would also expect.
The mass of the X-ray emitting gas is given approximately by
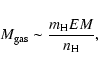 |
(2) |
where EM is the emission measure from X-ray observations and 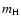 the hydrogen mass.
We have taken the emission measure from Hasinger et al.
(1996) with
the hydrogen mass.
We have taken the emission measure from Hasinger et al.
(1996) with
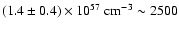 days after outburst
and extrapolated this result with t2.06 (see Appendix A) to 4000 days.
Using Eq. (2) we derive a gas mass of
days after outburst
and extrapolated this result with t2.06 (see Appendix A) to 4000 days.
Using Eq. (2) we derive a gas mass of
![$1.0\times 10^{-2}/n_{\rm H}[300~{\rm cm^{-3}}]~{M_{\odot}}$](/articles/aa/full/2002/43/aa2642/img137.gif) .
Overall,
this yields a dust-to-gas ratio in the range
.
Overall,
this yields a dust-to-gas ratio in the range
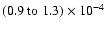 .
.
If the grain size distribution is allowed to extend to grains with
radii much larger than
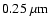 the acceptable fits imply that the dust-to-gas ratio could be as high as
the acceptable fits imply that the dust-to-gas ratio could be as high as
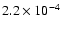 .
As will be seen in Sect. 4 the pre-supernova dust abundance would however
be almost unaffected.
.
As will be seen in Sect. 4 the pre-supernova dust abundance would however
be almost unaffected.


Up: Infrared emission towards SN 1987A
Copyright ESO 2002
![]() ,
where
,
where ![]() is the number of free parameters.
The best fits obtained for the two mixtures are shown in Fig. 4 together
with the fitted spectrum for silicate grains.
The emission spectrum is such that
measurements at longer wavelengths (e.g. Lundqvist et al. 1999)
are too insensitive to probe the emission from this region.
The fits can be summarised as follows:
is the number of free parameters.
The best fits obtained for the two mixtures are shown in Fig. 4 together
with the fitted spectrum for silicate grains.
The emission spectrum is such that
measurements at longer wavelengths (e.g. Lundqvist et al. 1999)
are too insensitive to probe the emission from this region.
The fits can be summarised as follows:
![]() the acceptable fits imply that the dust-to-gas ratio could be as high as
the acceptable fits imply that the dust-to-gas ratio could be as high as
![]() .
As will be seen in Sect. 4 the pre-supernova dust abundance would however
be almost unaffected.
.
As will be seen in Sect. 4 the pre-supernova dust abundance would however
be almost unaffected.