Here, we make some first numerical tests for the MS evolution of
a fastly rotating 40 ![]() star, with an initial rotation velocity
star, with an initial rotation velocity
![]() km s-1. This value of the initial rotation
leads to an average rotation during the MS phase of
440 km s-1 in the anisotropic case and to 320 km s-1 in the isotropic case.
For this stellar mass,
the opacity during the MS phase is produced by electron scattering.
This means that we consider a rotating star where the anisotropy
of the mass the flux given by Eq. (30) behaves like
km s-1. This value of the initial rotation
leads to an average rotation during the MS phase of
440 km s-1 in the anisotropic case and to 320 km s-1 in the isotropic case.
For this stellar mass,
the opacity during the MS phase is produced by electron scattering.
This means that we consider a rotating star where the anisotropy
of the mass the flux given by Eq. (30) behaves like
![]() .
As a consequence, the higher effective gravity
and
.
As a consequence, the higher effective gravity
and
![]() at the pole imply an enhanced polar
mass ejection. Other models of lower
at the pole imply an enhanced polar
mass ejection. Other models of lower
![]() with an equatorial ring ejection, like
expected for Be stars, and the various instabilities it
may create (like an equatorial convective torus due to Solberg-
Hoiland criterion) will be investigated in a further study.
with an equatorial ring ejection, like
expected for Be stars, and the various instabilities it
may create (like an equatorial convective torus due to Solberg-
Hoiland criterion) will be investigated in a further study.
Care has to be given that the radius given by the
integration of the equation of stellar structure
for rotating stars as given by Meynet & Maeder
(1997) is not the polar radius appearing
in Eq. (26), but a radius
![]() where
V is the volume of the distorded star.
For most velocities, this radius r* is equal
to the radius r(P2) at an average latitude
given by
where
V is the volume of the distorded star.
For most velocities, this radius r* is equal
to the radius r(P2) at an average latitude
given by
![]() ,
where
P2 is the second Legendre polynomial. At
,
where
P2 is the second Legendre polynomial. At
![]() ,
r* is larger by 0.7% than r(P2), at
,
r* is larger by 0.7% than r(P2), at
![]() ,
the difference reaches 1.7%.
,
the difference reaches 1.7%.
In usual models, a very accurate description
of the ![]() - and
- and ![]() -gradients at the edge of
the convective core is necessary, because this determines the transport
of chemical elements and mixing.
When anisotropic winds are included as here, we need in addition to
have a very accurate description of the
-gradients at the edge of
the convective core is necessary, because this determines the transport
of chemical elements and mixing.
When anisotropic winds are included as here, we need in addition to
have a very accurate description of the ![]() -profile
near the stellar surface, so as to properly describe the
inward transport of angular momentum by diffusion and circulation.
This requires very thin shells near the stellar surface, as well
as very short time steps, which enormously increases the computation time.
-profile
near the stellar surface, so as to properly describe the
inward transport of angular momentum by diffusion and circulation.
This requires very thin shells near the stellar surface, as well
as very short time steps, which enormously increases the computation time.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS2544f2.eps} \end{figure}](/articles/aa/full/2002/35/aa2544/Timg121.gif) |
Figure 2:
Illustration of the anisotropy of the mass flux
given by Eq. (30)
with colatitude during the MS evolution of a 40 |
In practice, we have found that in order to obtain results which are strictly
independent of the time steps ![]() (which is more than desirable!), it is
necessary that within one
(which is more than desirable!), it is
necessary that within one ![]() ,
the star loses only a small fraction
of the outermost shell mass,
,
the star loses only a small fraction
of the outermost shell mass,
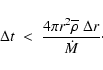 |
(38) |
Figure 1 illustrates the evolution of the shape of the model
star during its MS phase. We notice the growth
of the stellar radius and the increase of the flattening of the star
as it is moving away from the zero age sequence. At the middle of the
H-burning phase, the ratio of the equatorial to the polar radius is
about 1.2.
The variation of
![]() over the stellar surface shown in Fig. 1
leads to the anisotropy of the mass flux
(see also Pelupessy et al. 2000). The changes of the mass flux
over the stellar surface shown in Fig. 1
leads to the anisotropy of the mass flux
(see also Pelupessy et al. 2000). The changes of the mass flux
![]() as a function of the colatitude
as a function of the colatitude ![]() are illustrated in Fig. 2 for the corresponding evolutionary
stages during the MS phase. We notice that despite the
fact that there is no change of opacities over the stellar
surface, the anisotropy is becoming rather large. In the present
example, we see that the polar flux becomes equal to about 2.5 times
the equatorial flux.
Such anisotropies are sufficient to produce asymmetric nebulae
around hot star (cf. Lamers et al. 2001;
Maeder & Desjacques 2000). For a star
approaching the break-up velocity, the ratio of the polar to the equatorial
are illustrated in Fig. 2 for the corresponding evolutionary
stages during the MS phase. We notice that despite the
fact that there is no change of opacities over the stellar
surface, the anisotropy is becoming rather large. In the present
example, we see that the polar flux becomes equal to about 2.5 times
the equatorial flux.
Such anisotropies are sufficient to produce asymmetric nebulae
around hot star (cf. Lamers et al. 2001;
Maeder & Desjacques 2000). For a star
approaching the break-up velocity, the ratio of the polar to the equatorial
![]() may even become larger. However, at the same time
the equatorial opacity would grow a lot and the resulting
changes of the force multipliers, in particular of
may even become larger. However, at the same time
the equatorial opacity would grow a lot and the resulting
changes of the force multipliers, in particular of ![]() ,
would also
drive some strong equatorial ejection. Some models of ejected
shells have been made by Maeder & Desjacques (2000).
,
would also
drive some strong equatorial ejection. Some models of ejected
shells have been made by Maeder & Desjacques (2000).
In a stationary situation
the boundary condition given by Eq. (19) determines a certain
value of
![]() at the stellar
surface corresponding
to the torque
at the stellar
surface corresponding
to the torque
![]() .
This
.
This ![]() -
gradient can be established over a certain thickness in the very outer layers,
only if the mass loss is low enough (cf. Eq. (10)), so that the concerned layers
have not been ejected. Thus, such stationary situations do not apply
to OB stars, but to lower mass stars and in particular to solar mass stars in case
of magnetic braking.
-
gradient can be established over a certain thickness in the very outer layers,
only if the mass loss is low enough (cf. Eq. (10)), so that the concerned layers
have not been ejected. Thus, such stationary situations do not apply
to OB stars, but to lower mass stars and in particular to solar mass stars in case
of magnetic braking.
In a star with no or little mass loss, the application of the
full Eq. (6) should lead to the same result
for the behaviour of ![]() near the surface as the boundary condition (19).
As a test, we have made some
numerical calculations with small time steps
and a high number of shells near the surface of a 60
near the surface as the boundary condition (19).
As a test, we have made some
numerical calculations with small time steps
and a high number of shells near the surface of a 60 ![]() model at the beginning of the MS phase with an
initial v = 300 km s-1. We account
for the complete Eq. (6) at the surface
and apply the torque
model at the beginning of the MS phase with an
initial v = 300 km s-1. We account
for the complete Eq. (6) at the surface
and apply the torque
![]() corresponding to the anisotropic mass loss which would normally exist.
However, in order to test the boundary condition (19)
we arbitrarily keep the total stellar mass constant.
corresponding to the anisotropic mass loss which would normally exist.
However, in order to test the boundary condition (19)
we arbitrarily keep the total stellar mass constant.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS2544f3.eps} \end{figure}](/articles/aa/full/2002/35/aa2544/Timg126.gif) |
Figure 3:
Numerical tests showing the convergence of
|
Figure 3 shows some successive distributions of
![]() near the stellar surface with time intervals of 2000 years.
We notice the convergence
of
near the stellar surface with time intervals of 2000 years.
We notice the convergence
of
![]() toward a limiting curve in
a few thousand years. As expressed by
Eq. (19), for a polar enhanced mass loss we have
toward a limiting curve in
a few thousand years. As expressed by
Eq. (19), for a polar enhanced mass loss we have
![]() and
this is what we observe in Fig. 3. In addition,
we verify that the value of the slope
and
this is what we observe in Fig. 3. In addition,
we verify that the value of the slope
![]() corresponds to that given
by the stationary boundary condition (19).
The time necessary for establishing a stationary situation is
in this case of the order of about 6000 yr, i.e. much longer
that the time step
corresponds to that given
by the stationary boundary condition (19).
The time necessary for establishing a stationary situation is
in this case of the order of about 6000 yr, i.e. much longer
that the time step
![]() a few 10 yr. during which one layer
is going away.
This shows that the boundary condition given by
Eq. (19) may offer a consistent solution,
only if the mass loss is very small.
In particular, in lower mass stars
there is largely enough time for a stationary gradient to
be established by diffusion and circulation currents,
because the considered
layers are almost staying indefinitely in the star.
a few 10 yr. during which one layer
is going away.
This shows that the boundary condition given by
Eq. (19) may offer a consistent solution,
only if the mass loss is very small.
In particular, in lower mass stars
there is largely enough time for a stationary gradient to
be established by diffusion and circulation currents,
because the considered
layers are almost staying indefinitely in the star.
For O and early B-type stars, it is necessary to
apply the full Eq. (6) for the boundary condition
on the transport of angular momentum, with very
thin shells and small time steps as mentioned above. A positive ![]() -
gradient may appear over a number outer layers as a result of a positive
external torque. Of course, the full Eq. (6) must be applied
to the extreme non stationary
situations, like those of the
LBV stars, where the
-
gradient may appear over a number outer layers as a result of a positive
external torque. Of course, the full Eq. (6) must be applied
to the extreme non stationary
situations, like those of the
LBV stars, where the ![]() and
and ![]() limits can be
reached (cf. Maeder & Meynet 2000), or to the case of Be-stars
where an equatorial shell ejection may occur.
limits can be
reached (cf. Maeder & Meynet 2000), or to the case of Be-stars
where an equatorial shell ejection may occur.
Finally, we note that when a positive gradient
![]() like that in
Fig. 3 can be established, it also influences the
meridional circulation in the outer layers. U(r) is
zero at the surface, but it can become positive over
a small interval below the surface, before becoming negative in somehow deeper
layers due to the Gratton-Öpik term (cf. Meynet & Maeder 2000) and positive again in the deepest
radiative layers surrounding the convective core. In this
case, there could be 3 cells of meridional circulation
between the core and the surface. The two cells with U(r) > 0 are
rising along the rotational axis, while the intermediate cell with the negative
U(r) is descending along the polar axis. Thus, the account for an external
torque may modify the pattern of circulation currents.
like that in
Fig. 3 can be established, it also influences the
meridional circulation in the outer layers. U(r) is
zero at the surface, but it can become positive over
a small interval below the surface, before becoming negative in somehow deeper
layers due to the Gratton-Öpik term (cf. Meynet & Maeder 2000) and positive again in the deepest
radiative layers surrounding the convective core. In this
case, there could be 3 cells of meridional circulation
between the core and the surface. The two cells with U(r) > 0 are
rising along the rotational axis, while the intermediate cell with the negative
U(r) is descending along the polar axis. Thus, the account for an external
torque may modify the pattern of circulation currents.
The positive ![]() -gradient which arises from
polar mass loss enhances the stability with respect to the
Solberg-Hoiland criterion for convective-like instabilities
in rotating stars. Thus, the positive
-gradient which arises from
polar mass loss enhances the stability with respect to the
Solberg-Hoiland criterion for convective-like instabilities
in rotating stars. Thus, the positive
![]() resulting from polar mass loss in OB stars
brings no peculiar structural problems. This would not be true for
equatorial mass loss. In this case, the negative
resulting from polar mass loss in OB stars
brings no peculiar structural problems. This would not be true for
equatorial mass loss. In this case, the negative
![]() -gradient created by the equatorial mass loss
may, according to the Solberg-Hoiland criterion, lead to convective
instabilities in the outer equatorial layers.
Such problems will be considered in a future work in
relation with the case of Be-stars.
-gradient created by the equatorial mass loss
may, according to the Solberg-Hoiland criterion, lead to convective
instabilities in the outer equatorial layers.
Such problems will be considered in a future work in
relation with the case of Be-stars.
We examine some evolutionary consequences of the anisotropic mass loss with
the above model of a 40 ![]() with the standard Pop. I composition
Z=0.02 and X=0.705 with
with the standard Pop. I composition
Z=0.02 and X=0.705 with
![]() km s-1.
The mass loss rates for zero rotation are those by Vink et al.
(2000), which are much smaller than those by Lamers &
Cassinelli (1996) used in Paper V (Meynet & Maeder 2000).
Equation (34) is applied
to get the global mass loss rate corresponding to the actual rotation
at each time during evolution.
km s-1.
The mass loss rates for zero rotation are those by Vink et al.
(2000), which are much smaller than those by Lamers &
Cassinelli (1996) used in Paper V (Meynet & Maeder 2000).
Equation (34) is applied
to get the global mass loss rate corresponding to the actual rotation
at each time during evolution.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS2544f5.eps} \end{figure}](/articles/aa/full/2002/35/aa2544/Timg132.gif) |
Figure 5:
Evolution of the ratio
|
Due to the polar enhanced mass loss in O-stars, there is less angular momentum lost
for the anisotropic than for the isotropic mass loss.
As a consequence, the internal distribution of ![]() is
slightly flatter for models with
anisotropic winds than for models with isotropic winds. The reason is simple:
since there is less angular momentum removed in the anisotropic winds
of OB stars, the difference of
is
slightly flatter for models with
anisotropic winds than for models with isotropic winds. The reason is simple:
since there is less angular momentum removed in the anisotropic winds
of OB stars, the difference of ![]() between the
surface and the center is slightly smaller. However,
these effects are small and
the mixing of the chemical elements is the same in the two types of models.
between the
surface and the center is slightly smaller. However,
these effects are small and
the mixing of the chemical elements is the same in the two types of models.
Figure 4 shows the time evolution of the equatorial rotational velocity v at the stellar surface for the isotropic and anisotropic cases during the MS phase. The case of a rotating star with the same initial velocity of 500 km s-1, but without mass loss, is also shown, (this is not a model with solid body rotation; shear diffusion and meridional circulation are accounted for in this model). We notice the large differences in the evolution of v between these 3 cases. The standard case of isotropic mass loss leads to a fastly decreasing velocity, because the isotropic mass loss is taking a lot of angular momentum away as shown by Meynet & Maeder (2000). The growth of the mass loss rates as the star is evolving makes the decrease of v faster as the evolution proceeds. At the opposite, a model of massive star without mass loss rapidly reaches the break-up velocity. The reason is that the stellar concentration increases and the total momentum of inertia is decreasing. As a matter of fact, this last case leads to results which are not very different from those of a solid body rotating model (cf. Langer 1997), because in massive stars with a high rotation the internal coupling by circulation is very efficient. As we may have expected, the case of anisotropic mass loss is intermediate bewtween the case of no mass loss and that of isotropic mass loss. The difference between the isotropic and anisotropic cases is growing with time.
Figure 5 shows the time evolution of the ratio
![]() of the angular velocity to the critical angular velocity
for the same 3 cases shown in Fig. 4. We see that, after an age of
of the angular velocity to the critical angular velocity
for the same 3 cases shown in Fig. 4. We see that, after an age of
![]() yr,
this ratio is fastly decreasing
for the isotropic mass loss,
because due to the lower
yr,
this ratio is fastly decreasing
for the isotropic mass loss,
because due to the lower
![]() of the model the mass
loss rates are rapidly increasing. At the end of the MS phase, at an age of
of the model the mass
loss rates are rapidly increasing. At the end of the MS phase, at an age of
![]() yr the rotation velocity is only about 100 km s-1.
The case of the rotating model without
mase loss is reaching the break-up velocity. Interestingly enough
the model with anisotropic mass loss is also reaching the break-up velocity at an age
a bit larger than in the previous case. Thus, the account for anisotropies makes here
a big difference with respect to the case of isotropic mass loss:
instabilities
may be generated, heavy mass loss will result, an equatorial shell will be
ejected and the further evolution may be rather different.
yr the rotation velocity is only about 100 km s-1.
The case of the rotating model without
mase loss is reaching the break-up velocity. Interestingly enough
the model with anisotropic mass loss is also reaching the break-up velocity at an age
a bit larger than in the previous case. Thus, the account for anisotropies makes here
a big difference with respect to the case of isotropic mass loss:
instabilities
may be generated, heavy mass loss will result, an equatorial shell will be
ejected and the further evolution may be rather different.
The influence of the anisotropic mass loss is in general higher
for faster rotation, also its importance is varying with stellar mass.
For lower stellar masses, the mass loss rates are smaller and thus
all the effects related to mass loss are smaller, including the effect
of anisotropies. For very high masses
with very high mass loss rates, it happens as discussed in Sect. 2
that the most external layers
are removed before they have the time to convey the extra-torque
toward the stellar interior. Tests show that the internal effects
of anisotropies are negligible at 120 ![]() ,
as well as in LBV and WR stars
which have very high mass loss rates. At 60
,
as well as in LBV and WR stars
which have very high mass loss rates. At 60 ![]() and for an average MS
velocity of 300 km s-1, the difference of velocity at the middle of the MS
for the two cases of isotropic and anisotropic mass loss amounts to about 20 km s-1.
Basically, these first tests indicate that the effects of mass loss anisotropies
are significant between 25 and 60
and for an average MS
velocity of 300 km s-1, the difference of velocity at the middle of the MS
for the two cases of isotropic and anisotropic mass loss amounts to about 20 km s-1.
Basically, these first tests indicate that the effects of mass loss anisotropies
are significant between 25 and 60 ![]() when the average velocity
on the MS is larger than 300 km s-1.
Further grids of models will include the effects of anisotropies
and explore their
size over the HR diagram.
when the average velocity
on the MS is larger than 300 km s-1.
Further grids of models will include the effects of anisotropies
and explore their
size over the HR diagram.
If a star during its evolution reaches a rotational velocity close to the break-up velocity, this will enhance the mass loss according to Eq. (34). Thus at lower metallicity Z, the stars have initially less mass loss due to weaker stellar winds, and thus they may reach the break-up velocity. Paradoxically this will produce enhancements of the mass loss rates, which may become very large for stars close to the Eddington limit.
Let us also remark that for massive stars with large enough ![]() ,
i.e.
,
i.e.
![]() ,
the break-up velocity is even reached
for
,
the break-up velocity is even reached
for
![]() ,
a situation which
was called the
,
a situation which
was called the ![]() - or the
- or the
![]() -limit (cf. Langer 1997; Maeder & Meynet
2000). At the
-limit (cf. Langer 1997; Maeder & Meynet
2000). At the
![]() - limits, the star may undergo
extremely high mass loss rates, which may appear as outbursts.
Detailed modelisations of such events may be interesting.
Let us finally mention that
at the
- limits, the star may undergo
extremely high mass loss rates, which may appear as outbursts.
Detailed modelisations of such events may be interesting.
Let us finally mention that
at the
![]() - limit, the expressions (30) and (34) well describes
the growth of the mass flux and of the overall mass loss, because
in this case the process is a radiative one. On the contrary,
at the strictly speaking
- limit, the expressions (30) and (34) well describes
the growth of the mass flux and of the overall mass loss, because
in this case the process is a radiative one. On the contrary,
at the strictly speaking ![]() -limit (i.e. when
-limit (i.e. when ![]() is
smaller than 0.639 and that the instability is reached only due to the fact that
is
smaller than 0.639 and that the instability is reached only due to the fact that
![]() ), the mass loss is not
due to the radiation field and there is
no detailed prediction for the mass loss rate in this case, although
it is likely that the star keeps at the verge of the break-up limit
(cf. Langer 1997).
), the mass loss is not
due to the radiation field and there is
no detailed prediction for the mass loss rate in this case, although
it is likely that the star keeps at the verge of the break-up limit
(cf. Langer 1997).
Figure 6 shows the HR diagram for the 40 ![]() model
with v = 0 km s-1 and mass loss, and with
model
with v = 0 km s-1 and mass loss, and with
![]() km s-1 for the 3 cases
of isotropic, anisotropic and zero mass loss.
We recall that in general there is an increase of the
lifetimes produced by fast rotation, since the reservoir
of available hydrogen is increased by rotation.
In the present case, the MS lifetime until
km s-1 for the 3 cases
of isotropic, anisotropic and zero mass loss.
We recall that in general there is an increase of the
lifetimes produced by fast rotation, since the reservoir
of available hydrogen is increased by rotation.
In the present case, the MS lifetime until
![]() is
is
![]() yr. for the model with
yr. for the model with
![]() km s-1 and it is
km s-1 and it is
![]() yr. for the the model with
yr. for the the model with
![]() km s-1 and isotropic mass loss, i.e.
27% larger. The various tracks show significant differences.
In the case with v = 0 km s-1, the track is similar to those shown
by Meynet & Maeder (2000). For
km s-1 and isotropic mass loss, i.e.
27% larger. The various tracks show significant differences.
In the case with v = 0 km s-1, the track is similar to those shown
by Meynet & Maeder (2000). For
![]() km s-1
and isotropy, the track is going upwards to higher luminosity due to the strong
mixing and the associated growth of the core. This model is keeping at
a higher
km s-1
and isotropy, the track is going upwards to higher luminosity due to the strong
mixing and the associated growth of the core. This model is keeping at
a higher
![]() ,
because mixing is bringing to the surface a lot of helium
which lowers the opacity. The two models which reach critical velocity
are shifted to the red due to the large atmospheric extension due to
high rotation. These two models are followed here only until they reach
their critical velocity, because the evolution and tracks for the star
models reaching break-up
very much depends on the way the losses of mass and
angular momentum are treated in the critical phase. This will be further
studied in forthcoming papers. For now, we just note that
when the luminosity is
,
because mixing is bringing to the surface a lot of helium
which lowers the opacity. The two models which reach critical velocity
are shifted to the red due to the large atmospheric extension due to
high rotation. These two models are followed here only until they reach
their critical velocity, because the evolution and tracks for the star
models reaching break-up
very much depends on the way the losses of mass and
angular momentum are treated in the critical phase. This will be further
studied in forthcoming papers. For now, we just note that
when the luminosity is
![]() ,
the central hydrogen content
is larger for the models shifted to the right, i.e. from the model with
zero rotation to the models with the highest rotation and therefore highest
internal mixing. The stronger mixing keeps the central hydrogen
higher.
,
the central hydrogen content
is larger for the models shifted to the right, i.e. from the model with
zero rotation to the models with the highest rotation and therefore highest
internal mixing. The stronger mixing keeps the central hydrogen
higher.
Copyright ESO 2002