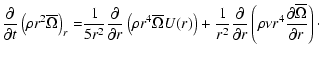 |
(1) |
The above equation expresses that the change of angular momentum of
a certain mass element in a star results from the transport by the meridional
circulation with a velocity U(r) and from the turbulent diffusion
with a coefficient ![]() .
If U(r) and
.
If U(r) and ![]() are zero, this equation
just says that the specific angular momentum
are zero, this equation
just says that the specific angular momentum
![]() of a mass element
remains constant. The expression for U(r) is that given by
Maeder & Zahn (1998) and for
of a mass element
remains constant. The expression for U(r) is that given by
Maeder & Zahn (1998) and for ![]() by
Maeder & Meynet (2001).
by
Maeder & Meynet (2001).
If the anisotropic stellar winds remove some matter, for example, at the
pole, the lack of mass, say the "hole'' at the pole, will be
filled almost instantaneously by some material moving horizontally
on the equipotential and bringing its angular momentum.
Indeed, the timescale for this compensation is very short.
It is the local dynamical timescale,
of the orders of hours or days at most in massive stars.
Thus, the equation of the surface will always be an equipotential,
given for example by the Roche model. However,
in the above example the polar mass loss removes less angular momentum
than the corresponding amount of mass lost spherically. Let us call
![]() the difference of the
angular momentum lost by unit of time
between an anisotropic stellar wind and a spherical wind for the same
amount of mass loss in a star of given angular velocity
the difference of the
angular momentum lost by unit of time
between an anisotropic stellar wind and a spherical wind for the same
amount of mass loss in a star of given angular velocity
![]()
Whether anisotropic mass loss is present or not, the basic Eq. (1)
for the conservation of angular momentum remains the same in the stellar
interior. The external torque
![]() due to an anistropic mass loss
is only directly acting on the outer surface layer.
This means that the modifications of the system of equations
only concern the outer boundary conditions. Of course
indirectly, the change of boundary conditions can affect the
internal distribution of
due to an anistropic mass loss
is only directly acting on the outer surface layer.
This means that the modifications of the system of equations
only concern the outer boundary conditions. Of course
indirectly, the change of boundary conditions can affect the
internal distribution of
![]() ,
the patterns of meridional circulation,
the evolution, etc.
,
the patterns of meridional circulation,
the evolution, etc.
Focusing on the outer boundary conditions,
we integrate Eq. (1) over the last thin shell of
mass
![]() centered at a level r just below the stellar surface.
We get with account for the anisotropic loss of angular
momentum by stellar winds at the surface,
centered at a level r just below the stellar surface.
We get with account for the anisotropic loss of angular
momentum by stellar winds at the surface,
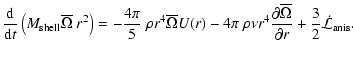 |
(3) |
| (4) |
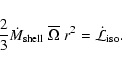 |
(5) |
For polar mass loss, the contribution to the rotation of the
outer shell is positive, i.e.
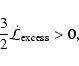 |
(7) |
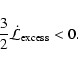 |
(8) |
We insist on the fact that Eq. (6) is not just a
mathematical trick to account for the anisotropic mass loss, but it
closely corresponds to the physical conditions in the case of
anisotropic mass loss. Let us, for example, consider the case
of polar enhanced mass loss. As said above, the mass removed by stellar
winds at the pole will be almost instantaneously replaced
by a flow of material coming from equatorial regions
on the equipotential. This material will have more
angular momentum than the average material on the equipotential
and thus it
exerts a positive torque on the
surface layer, enhancing its rotation. The strong horizontal turbulence
rapidly smears out the effect of this torque on the considered equipotential.
We do think that this one dimensional treatment of a physical problem,
which by essence is two dimensional, is a correct although simplified
representation. The two hypotheses, a) of the instantaneous replacement of the matter
on a surface layer and b) that this layer is preserving its equipotential shape,
do not seem unreasonable in view of the considered dynamical timescales.
Of course, very critical would be the presence of magnetic field
which would introduce some coupling of the surface layer
both upwards with the ejected matter and downwards with the layers below,
as well as horizontally on the equipotential.
In this context, let us note that Eq. (6) can also be applied in
stars, which are slowed down by magnetic braking. In this case the
quantity
![]() is
the torque exerted by the magnetic field.
is
the torque exerted by the magnetic field.
There is an additional
problem in massive stars. If the mass loss is high, the outer layers
are removed before the transport of angular momentum by circulation
and turbulent diffusion has the time to bring the angular momentum inward.
The condition for the transport of angular momentum to occur
is that the characteristic time
![]() for the readjustement of
for the readjustement of
![]() by circulation and diffusion is
shorter than the caracteristic timescale
by circulation and diffusion is
shorter than the caracteristic timescale
![]() for mass loss, i.e.
for mass loss, i.e.
Copyright ESO 2002