| |
(11) |
This solution applies to the outer boundary of
the radiative zone in solar type stars, which have an external
convective zone.
An asymptotic regime, where the wind properties vary only slowly,
on a time long with respect to the characteristic time of meridional
circulation is considered by Zahn (1992). He also
assumes, which is well verified, that the momentum of inertia
of the boundary layer is negligible, so that the flux of angular momentum
is nearly constant with depth. Thus, the time derivative in
Eq. (6) is zero. In addition, Zahn assumes
that the angular momentum transported by the turbulent viscosity is
negligible with respect to the advection, an assumption which is
also verified in the interior. Thus, one has
If
![]() ,
as it would be produced for
example by the magnetic braking in solar type stars, then one has
U(r) < 0 near the outer edge of the radiative zone.
This means that
the lack of angular momentum at the edge
will be compensated by a meridional circulation flow
descending along the polar axis and ascending at the equator.
It may be surprising to have a non zero U(r) at the outer boundary. But
as pointed by Zahn (1992), there is no problem since in solar
type stars the outer convective zone allows the return
of mass and its conservation.
,
as it would be produced for
example by the magnetic braking in solar type stars, then one has
U(r) < 0 near the outer edge of the radiative zone.
This means that
the lack of angular momentum at the edge
will be compensated by a meridional circulation flow
descending along the polar axis and ascending at the equator.
It may be surprising to have a non zero U(r) at the outer boundary. But
as pointed by Zahn (1992), there is no problem since in solar
type stars the outer convective zone allows the return
of mass and its conservation.
Future works will tell us whether the above boundary conditions
are well appropriate for solar type stars. In the case of
Main Sequence (MS) stars with outer radiative layers,
the above boundary conditions
do not apply for two reasons. Firstly, with a non zero value of
U(r) the return of mass is not insured; one cannot
consider that the mass loss insures the mass continuity,
because stellar winds in massive
stars are present independently of the sign of U(r). Secondly,
we may not consider that
![]() ,
since the positive or negative torque exerted by
,
since the positive or negative torque exerted by
![]() in the case of anisotropic stellar winds
will create a gradient of
in the case of anisotropic stellar winds
will create a gradient of
![]() in the outer layers. Thus, more appropriate boundary
conditions have to be found.
in the outer layers. Thus, more appropriate boundary
conditions have to be found.
The content of angular momentum of the outer shell is relatively very small,
or in other words there is no possibility of stockage in the outer
shell. Thus a situation of equilibrium may be reached between the
gain (or loss)
![]() of angular momentum
due to the anisotropic loss and the transport due to advection or diffusion
toward (or from) the deeper layers.
Thus, we consider that in the external shell the
time derivative in the first member
of Eq. (6) is zero and we have
of angular momentum
due to the anisotropic loss and the transport due to advection or diffusion
toward (or from) the deeper layers.
Thus, we consider that in the external shell the
time derivative in the first member
of Eq. (6) is zero and we have
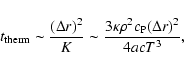 |
(14) |
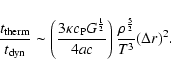 |
(15) |
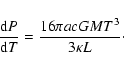 |
(16) |
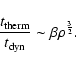 |
(17) |
As shown by Eqs. (9) and (10), the mass loss rates must
not be too large in order that the outer layers
are not removed before they have had the
time to transport the angular momentum. This requirement is even much more
severe for an equilibrium stage to be established and we may estimate that
mass loss rates smaller by about 2 orders of a magnitude with respect
to
![]() are necessary for this. In view of the estimate
given after Eq. (10), this means that the mass loss rates must likely be smaller
than
are necessary for this. In view of the estimate
given after Eq. (10), this means that the mass loss rates must likely be smaller
than ![]() 10
10
![]() yr-1, which corresponds to
stellar mass lower than about 15
yr-1, which corresponds to
stellar mass lower than about 15 ![]() .
These are rough estimates and
future grids of models may further precise these values.
.
These are rough estimates and
future grids of models may further precise these values.
Copyright ESO 2002