4 One-dimensional model

4.1 Why a cellular automata

The use of a wavelet decomposition of our synthetic velocity field gives access to the best approximation at any scale between the integral scale l₀ (where it is just the mean velocity, and is 0.0by construction) and the smallest accessible scale $l_{0}\: 2^{-N_{\max }}$, where $N_{\max}$ is the number of steps in the wavelet transform.

As we are interested in the effects of turbulence on the dynamics of a cloud, the smallest significant scale is the turbulence dissipation length. Any cell of gas smaller than that length is homogeneous and statistically identical to its nearest neighbour. That scale may be estimated from classical results on Kolmogorov turbulence (see Frisch 1995): the energy flux through scales is $\varepsilon =\frac{v^{3}}{l}$, which is true also at l_N, the Polaris resolution scale with v_N, the turbulent velocity at that scale. We can estimate that quantity from the observations if we take $\Delta v$, the standard deviation of centroids increments at scale l_N, as an estimate of v_N. From the Polaris map, $v_{N}=0.1\:{\rm km}~ {\rm s}^{-1}$, so that $\varepsilon =3\times 10^{-5}\: {\rm cm}^{2}~{\rm s}^{-3}$. Then the dissipation scale is given by $\eta =\left( \frac{\nu ^{3}}{\varepsilon }\right) ^{1/4}$, where $\nu$ is the kinematic viscosity. In a diluted gas, $\nu \simeq \frac{v_{\rm th}}{n~ \sigma }$, where $v_{\rm th}$ is the thermal velocity, n the gas density, and $\sigma$ the collision cross section. Inside a molecular gas, we can take a mean ${\rm H}_{2}$- ${\rm H}_{2}$ cross section of $\sigma =1.5\times 10^{-14}\: \rm {cm}^{2}$ (see Le Bourlot et al. (1999)), a density of $10^{4}~{\rm cm^{-3}}$ and a temperature of $10~{\rm K}$. This gives:

$$\eta =7.5\times 10^{11}\left( \frac{n}{10^{4}}\right) ^{-3/4}... ...\right) ^{-1/4}\: \left( \frac{T}{10}\right) ^{3/8}\: {\rm cm}.$$

From l_N, we can proceed with the cascade process down to the smallest scale $l_{N_{\max }}$ that depends mainly on computational power. However, $\frac{l_{N}}{\eta }\sim 2^{15}$, which is still too much for us. We have chosen to stop the model at $l_{N_{\max }}=140$ AU ( $N_{\max }=17)$. The corresponding angular resolution at Polaris would be 0.94''. The associated time scale is $t_{N_{\max }}=\frac{l_{N_{\max }}}{v_{N_{\max }}}=5.25\times 10^{11}\: \rm {s}$(note that the effective velocity dispersion at that scale $v_{N_{\max }}\simeq 0.04~ {\rm km}~ {\rm s}^{-1}$is close to the value deduced from a constant $\varepsilon$up to that scale).

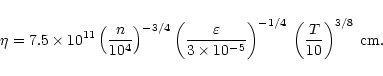
Since we are not interested in the physics inside that box, we can use a coarse-grained approximation by looking at a collection of identical cells of size $l_{N_{\max }}$, coupled by convection (hence our need to prescribe the velocity field) or radiatively (i.e. in velocity space nearest neighbour but not necessarily in physical space, see Rousseau et al. 1998). Thus, we by-pass the need to solve partial differential equations and need only to prescribe the evolution of mean variables inside each box and their mutual coupling (hereafter only by convection). The most accurate way to realise that smoothing is to use the approximation coefficients of the wavelet transform at that scale.

So we consider a set of identical boxes, each characterised by local dynamics (a set of local variables, coupled by physical relationships) with the same variables and evolution laws in each cell, but not necessarily the same initial conditions. Evolution is computed over a continuous time within each box, and a spatial coupling is applied at discrete times. The velocity at the smallest scale $l_{N_{\rm max}}$ is taken as the mean velocity of a box in a rest frame. Therefore we use an Eulerian representation. Velocity is prescribed a priori, and is not modified by the evolution of any local variable. It is understood that the way the velocity field is built takes care of all (mostly unknown) processes that constrain its evolution. What we need now is a way to progress in time.

4.2 Time dependence

As a first stage, our goal is to model a cloud in steady state. This means that all its statistical properties remain constant on average, but are not necessarily time independent! They may fluctuate in time around a mean value, and only that value is constant in time. This has to be true also for the velocity field, so that we need to prescribe the evolution in time of the static field of Sect. 3. To that end, we make the hypothesis that turbulence is homogeneous, isotropic, and stationary. Under these three conditions, the Taylor hypothesis applies and the statistical properties of  v(x₀,t) as t varies are the same as those of v(x,t₀) along an axis x. This hypothesis may be extended to a 1D structure: the statistical properties of a velocity field v(X,t) along an axis X as t varies are the same as that of a collection of lines in a 2D plane at a given time t₀. The second hypothesis is stronger than the first because cross-correlations between orthogonal directions X and Y have to be included and is only true if the three conditions of homogeneity, isotropy, and stationarity strictly apply, see Appendix A for a demonstration.

The extension to 2D of the velocity field generation algorithm is straightforward (although computationally intensive). Details are given in Arnéodo et al. (1999) and references therein (see Appendix C). Once a 2D X-Y field has been generated, the Y axis can be interpreted as u₀t, where u₀ is a "scanning'' velocity that sets a time scale for the model. For consistency, we take $u_{0}=v_{N_{\max }}$. From this point, the velocity in our model is prescribed in each box of size $\delta =l_{N_{\max }}=l_{0}~ 2^{-N_{\max }}$and at each time $t_{j}=j~ t_{N_{\max }}=j~ \frac{\delta }{v_{N_{\max }}}$(where $t_{N_{\max }}=5.25\times 10^{11}\: {\rm s}$ is the crossing time at the smallest scale).

  
4.3 Density field

Mass conservation reads:

$$\frac{\partial \rho }{\partial t}+\overrightarrow{\nabla }.(\rho \overrightarrow{v})=0.$$ (10)

Once the velocity field is known (which is our case), this equation becomes a linear PDE in only one unknown, $\rho$. It can be solved easily as soon as initial and boundary conditions are set. The system is dissipative and a typical stationary state is reached after a relaxation time of a few  $t_{N_{\max}}$ (with $t_{N_{\max }}=5.25\times 10^{11}\: {\rm s}$).

We use uniform initial conditions and assume periodic boundary conditions. Equation (10) is solved in each "box'' as a balance equation. We "count'' the total amount of matter that escapes and enters each box: namely, for three successive boxes (at step j, density $\rho ^{j}_{i-1}$, $\rho ^{j}_{i}$ and $\rho ^{j}_{i+1}$and velocity v^j_i-1, v^j_i and v^j_i+1, we have:

$$\rho ^{j+1}_{i}=\rho ^{j}_{i-1}\frac{v^{j}_{i-1}}{u_{0}}Y^{+}... ...}}\right) -\rho ^{j}_{i+1}\frac{v^{j}_{i+1}}{u_{0}}Y^{-}_{i+1}$$ (11)

where Y⁺_i=1 if v_i is positive, Y^-_i=1if v_i is negative, and both are zero otherwise. Within a time step , the number of sub-step k is chosen to ensure that stays lower than 1 (as a further development, the method may include asynchronous time integration). Note that the absolute value of the density scaling is arbitrary, since velocity evolution does not depend on it; all density fields follow the same evolution.

Figure 6: Relative difference (in %) in the standard deviation of the density field as a function of time for two different initial fields (constant initial density of 1 and random initial density in the range [0; 2]).

After a transitory period, the density and velocity fields "couple'' together and the standard deviation stabilises (the mean density is constant because periodic boundary conditions ensure conservation of the total mass). In Fig. 6 we have plotted the evolution (after the transitory period) of the relative difference in the standard deviation for two different initial density fields (random value on the interval [0; 2] and a constant initial density of 1): this relative difference maintains a very small value (typically 1%).

A typical example of a density field is given in the top panel of Fig. 7. We see that large fluctuations of are possible within a few cells and dense cores develop over a low-density background.

The density field obtained with our synthetic turbulent velocity field and the one obtained with a Gaussian velocity field of the same mean and standard deviation are very different (see Fig. 7): for the Gaussian field, the density seems relatively uniform but for the turbulent field, some structures appear naturally at all scales. Figure 8 shows the PDF of the logarithm of the density obtained with our synthetic turbulent velocity field. It is log-normal towards high density and exhibits a strong power law towards low density. The high density cut-off is a finite size effect, and the power law may be interpreted as an indication that our velocity field mimics that of a non-isothermal fluid, but we did not try to check that point further. This point will be dealt with in a further paper with an improved model, easier to compare to observations and hydrodynamical models.

Figure 7: Log of the density field for a turbulent and for a Gaussian velocity field (mean and standard deviation are the same for both fields).

Figure 8: Pdf of the logarithm of the density for our turbulent velocity field.

A relation between size and density can be computed: Using a Gaussian wavelet we compute for each scale the mean value of the density above the mean (which is here the same at all scales). Figure 9 shows a power law relation with an index of $-0.32\pm 0.03$. This is much lower than the $n \propto l^{-1}$ law that results from self-gravitating clouds. Such a flat index is probably a consequence of our 1D model and further discussions should wait for 2D results.

Figure 9: Decimal logarithm of the density as a function of scale.

  
4.4 Mixing of a passive scalar

Mixing properties of our synthetic velocity field may be derived from the evolution in time of the distribution of a passive scalar (say a non-reacting chemical species). The initial density is 1 in a single box located at x=256 and 0 elsewhere. The density after 1024 iterations (i.e. some 17 Myr) is shown Fig. 10 for two different velocity fields: a random Gaussian field (without correlations), and our synthetic turbulent field.

The resulting density profiles are quite different: a random Gaussian field leads to a localised Gaussian profile, whilst a turbulent field leads to a wider dispersion after a much shorter time (typically, the large-scale turnover time, here, about 1 Myr). As a check of our numerical procedure, we plot in Fig. 11 the mean position (relative to the initial maximum position) and standard deviation of the density profile obtained with the Gaussian velocity field. As expected, the mean position is a linear function of time ( $\overline{x}/\Delta x\approx v_{\rm {mean}}~ n~ \Delta t/\Delta x$, here $v_{\rm {mean}}~ \Delta t/\Delta x=-5.5\times 10^{-3}$and the fit gives $-4.5\times 10^{-3}$) and the standard deviation increases as the square root of time ( $\sigma _{x}/\Delta x\approx \sqrt{2Dn\Delta t}/\Delta x$with the diffusion coefficient $D=\sigma _{v}\Delta x/3$, here $\frac{2}{3}\sigma _{v}~ \Delta t/\Delta x=0.69$ and the result of the fit is 0.76). These results demonstrate that our lattice dynamical network is an accurate approximation of the diffusion equation.