

Up: Interstellar turbulent velocity fields: chemistry
Appendix C: 2D log-normal cascade
For any function
![\( f\in L_{\rm per}^{2}([0,L]^{2}) \)](/articles/aa/full/2002/27/aa2137/img171.gif) ,
f can be written
under the form
,
f can be written
under the form
The construction rule is the following: one generates the modulus
![\( d_{j,m,n}=\left( \left[ c_{j,m,n}^{1}\right] ^{2}+\left[ c^{2}_{j,m,n}\right] ^{2}+\left[ c^{3}_{j,m,n}\right] ^{2}\right) ^{1/2} \)](/articles/aa/full/2002/27/aa2137/img173.gif) of the wavelet coefficients in a recursive way by:
of the wavelet coefficients in a recursive way by:
Mj,m,n follows the prescribed log-normal law
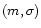 .
.
The wavelet coefficients themselves are computed via two angles
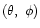 :
:
where 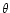 is randomly chosen between
is randomly chosen between
![\( [-\pi,~\pi ] \)](/articles/aa/full/2002/27/aa2137/img179.gif) and
and 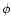 is randomly chosen between
is randomly chosen between
![\( \left[ -\phi ^{*},\phi ^{*}\right] \)](/articles/aa/full/2002/27/aa2137/img181.gif) where
where 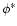 satisfies
satisfies
with
Finally, isotropy follows from adjusting the weights at the largest
scale:
c10,0,0 = d0,0,0,
c20,0,0 = d0,0,0,
and
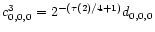 (see Decoster et al. 2000 for all details).
(see Decoster et al. 2000 for all details).


Up: Interstellar turbulent velocity fields: chemistry
Copyright ESO 2002
![]() ,
f can be written
under the form
,
f can be written
under the form
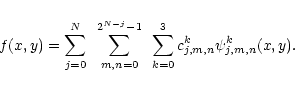
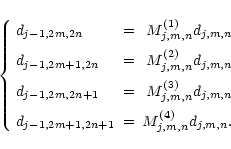
![]() :
:
![\begin{displaymath}\left\{ \begin{array}{lcl}
c^{1}_{j,m,n} & = & \cos(\phi )\co...
...m]
c^{3}_{j,m,n} & = & \sin(\phi )d_{j,m,n}
\end{array}\right. \end{displaymath}](/articles/aa/full/2002/27/aa2137/img177.gif)
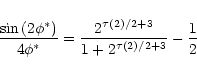
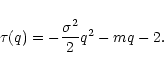
![]() (see Decoster et al. 2000 for all details).
(see Decoster et al. 2000 for all details).