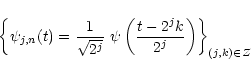 |
(6) |
We generate a velocity field by constructing its wavelet decomposition
coefficients. We use the concept of multi-resolution associated with
an orthogonal wavelet (see Mallat 1999): the dilated and translated
family
The standard deviation of the velocity field as a function of size
is plotted in Fig. 4. The law
![]() fits
both the synthetic velocity field and the Polaris region well with
an exponent of
fits
both the synthetic velocity field and the Polaris region well with
an exponent of
![]() in both cases. This exponent
is clearly irrelevant (or equal to 0) for a classical Gaussian field:
for such a field the standard deviation is the same for any scale;
the difference observed is just a sampling effect. The model is adjusted
to observations by fixing d0,0 so that the curves coincide.
Here,
d0,0=250 for 13 octaves (reductions of scale by a
factor of 2) between the integral scale and the
in both cases. This exponent
is clearly irrelevant (or equal to 0) for a classical Gaussian field:
for such a field the standard deviation is the same for any scale;
the difference observed is just a sampling effect. The model is adjusted
to observations by fixing d0,0 so that the curves coincide.
Here,
d0,0=250 for 13 octaves (reductions of scale by a
factor of 2) between the integral scale and the ![]() scale.
scale.
The resulting velocity field is then submitted to the same analysis
as the original one, and the number of steps between our integral
scale and the Polaris map scale is fixed by adjusting the non-Gaussian
wings. Figure 5 shows the resulting PDFs. Here N=13between the integral scale and the ![]() scale. Note that
the synthetic field PDFs are in good agreement with the observed ones,
and that the synthetic field is correlated at all scales (a rough
estimate of the synthetic signal correlation length at scale ais a) unlike the uncorrelated Gaussian field used for comparisons.
scale. Note that
the synthetic field PDFs are in good agreement with the observed ones,
and that the synthetic field is correlated at all scales (a rough
estimate of the synthetic signal correlation length at scale ais a) unlike the uncorrelated Gaussian field used for comparisons.
We are now able to determine the scaling of our model by identifying
size at scale N with Polaris resolution. In Fig. 5,
![]() pixels corresponds to
lN=2250 AU, so that
our integral scale is
pixels corresponds to
lN=2250 AU, so that
our integral scale is
![]() .
Note that this is not the size of the cloud that we generate: the
Polaris map size is reached after 9 steps in the generating process.
A side effect of that sub-sampling is that the mean global velocity
of the generated cloud is slightly non 0.0 (see Sect. 4.4).
.
Note that this is not the size of the cloud that we generate: the
Polaris map size is reached after 9 steps in the generating process.
A side effect of that sub-sampling is that the mean global velocity
of the generated cloud is slightly non 0.0 (see Sect. 4.4).
![\begin{figure}
\includegraphics[width=8.8cm,clip]{MS2137f5r.eps}
\end{figure}](/articles/aa/full/2002/27/aa2137/Timg61.gif) |
Figure 5: Comparison between the velocity increments' PDFs of the Polaris map (points) and the reconstructed field (lines) for different scales. |
Copyright ESO 2002