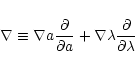Up: Global modes and migration
Appendix 2: The equations of motion in two dimensional
orthogonal cordinates
The basic equations of motion (1) written in vector form are
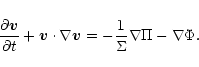 |
(78) |
We wish to write these in component form in a general two dimensional
orthogonal coordinate system
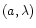 in the Cartesian (x,y)plane as introduced
in Sect. 5. The unit vectors in these orthogonal
coordinate directions
are
in the Cartesian (x,y)plane as introduced
in Sect. 5. The unit vectors in these orthogonal
coordinate directions
are
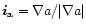 and
and
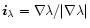 respectively.
The orthogonal vertical coordinate z has an additional associated
orthogonal unit vector
respectively.
The orthogonal vertical coordinate z has an additional associated
orthogonal unit vector
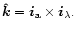 However, there is no dependence on z and the velocity component
in that direction can be taken to be zero.
However, there is no dependence on z and the velocity component
in that direction can be taken to be zero.
Thus we may write
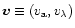 or
or
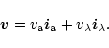 |
(79) |
To deal with Eq. (.78), we first use the vector identity
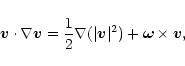 |
(80) |
where
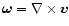 is the vorticity (Arfken & Weber 2000).
is the vorticity (Arfken & Weber 2000).
Because we only wish to consider the equations in a two dimensional
limit, only the z component of vorticity, 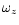 is non zero
so that we may write Eq. (.78) as
is non zero
so that we may write Eq. (.78) as
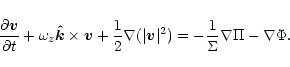 |
(81) |
We may now write Eq. (.81) in component form
using the identities (see Arfken & Weber 2000)
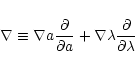 |
(82) |
and
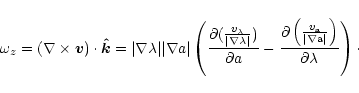 |
(83) |
Doing this we obtain
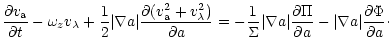 |
|
|
(84) |
and
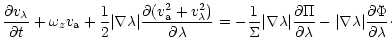 |
|
|
(85) |
After inserting (.83) into (.84) and (.85)
it is a simple matter to obtain
Eqs. (34) and (35) as given in Sect. 5.


Up: Global modes and migration
Copyright ESO 2002
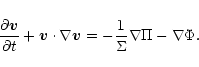
![]() or
or
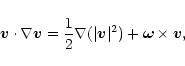
![]() is the vorticity (Arfken & Weber 2000).
is the vorticity (Arfken & Weber 2000).
![]() is non zero
so that we may write Eq. (.78) as
is non zero
so that we may write Eq. (.78) as