 |
(64) |
 |
(64) |
In order to incorporate the effects of protoplanets orbiting interior to the disc we adopt a Jacobi coordinate system. In this system the coordinates of the innermost protoplanet are referred to the central star. The coordinates of the remainder are referred to the centre of gravity of the central mass and all interior protoplanets. The disc is referred to the centre of mass of central star and all inner protoplanets.
This has the following consequences:
For an object interior to the
protoplanet with
![]() the acceleration of the coordinate system
due to the protoplanet must be allowed for. This gives rise,
correct to first order in
the acceleration of the coordinate system
due to the protoplanet must be allowed for. This gives rise,
correct to first order in
![]() to the indirect
potential (e.g. Brouwer & Clemence 1961)
to the indirect
potential (e.g. Brouwer & Clemence 1961)
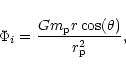 |
(65) |
For an object exterior to the protoplanet one must take account
of the fact that the coordinate system is now based on the centre of mass
of the inner protoplanets and central star. Assuming initially
that ![]() is the only such protoplanet, the central potential
is modified to become
is the only such protoplanet, the central potential
is modified to become
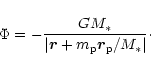 |
(66) |
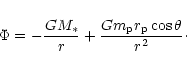 |
(67) |
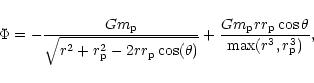 |
(68) |
In addition, although we included just one inner perturbing protoplanet, because we work to first order in their masses, the principle of linear superposition is valid such that the contributions of many such objects may be linearly superposed.
The perturbing
potential due to a single
protoplanet may be decomposed as a Fourier expansion in ![]()
Thus
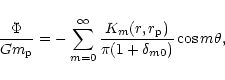 |
(69) |
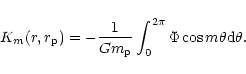 |
(70) |
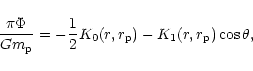 |
(71) |
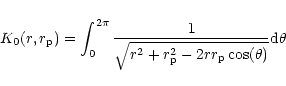 |
(72) |
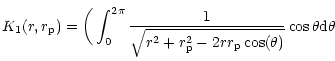 |
|||
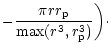 |
(73) |
Time averaged potential for a protoplanet with small eccentricity
We now suppose the protoplanet has a small eccentricity, ![]() and write for its motion
and write for its motion
![]() where without loss of generality
we assume the apsidal line to be along
where without loss of generality
we assume the apsidal line to be along
![]() where the displacement
where the displacement
![]() at t=0.
at t=0.
Here the protoplanet
semi-major axis is ![]() and the orbital frequency
is
and the orbital frequency
is ![]()
Expanding to first order in
![]() we find for the
single protoplanet perturbing potential
we find for the
single protoplanet perturbing potential
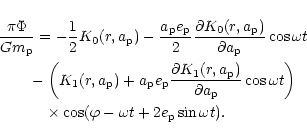
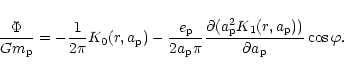 |
(74) |
For small ![]() we may replace
we may replace ![]() by
by ![]() and
expressing the result in terms of the radial
displacement
and
expressing the result in terms of the radial
displacement
![]() we find
we find
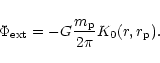 |
(76) |
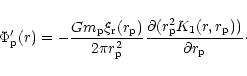 |
(77) |
Copyright ESO 2002