5 Correlations between lines

It is interesting to look for theoretical correlations between different radiative or plasma properties such as the integrated intensities, optical depths, electron temperature, or gas pressure. This helps us to understand the physical processes that are at work in the line formation. Such a task has been done by Heinzel et al. (1994) for the hydrogen spectrum in 1D isothermal isobaric prominence models. Our aim here is to look for correlations between integrated intensities. For clarity we have restricted our study to only one value of the prominence thickness (1000 km).

Figure 11: Half emergent line profiles for one slab width (1000 km) at 6000 K (four top panels) and 18000 K (four bottom panels). Solid line: P=0.02; dots: P=0.05; short dashes: P=0.1; long dashes/dots: P=0.2; long dashes: P=0.5. Same units as in Fig. 5.

Figure 12: Integrated intensities (in cgs units) for 4 lines as a function of the pressure computed for one slab width (1000 km) and 8 temperatures. Same symbols as in Fig. 6.

5.1 Helium triplet lines: E(10830) and E(D3)

We present in Fig. 16 the relation between $E(10\,830)$ and $E({\rm D}3)$ for 40 models with a slab thickness of 1000 km. This relation between these optically thin triplet lines is clearly linear. This linearity would only disappear in the case where at least one of the lines becomes optically thick and begins to saturate at line center. This may marginally happen for the 10830 line. In this case the ratio between the 10830 line intensity and another triplet line would slightly decrease. We stress that this linear relation is valid in the optically thin case for all the triplet lines we have studied. The only thing which varies from one line pair to another is of course the slope of the relation. This is due to the fact that in the triplet line source function the scattering term is dominant over the collisional term for a wide range of physical conditions. Thus the triplet line ratios mainly depend on the ratio of the incident line intensities. Here we obtain a constant ratio $E(10\,830)/E({\rm D}3) = 5.0$ for the 40 models represented in Fig. 16. In the following we will only consider the D3 line, keeping in mind that all the results presented for this line can easily be transposed to any other triplet line such as He I $\lambda\lambda$10830, 7065, 3889, 3188 or 4471 Å if the intensity ratio is known. Table 6 summarizes the different triplet line ratios for 40 models computed with $n_{\rm He}/n_{\rm H}=0.10$ and a slab thickness of 1000 km.

Figure 13: Mean population densities (in cm-3) as a function of the helium abundance for two different models: T=6000 K, P=0.02 dyn/cm2 and W=1000 km (top panel); $T=18\,000$ K, P=0.2 dyn/cm2 and W=1000 km (bottom panel). Solid lines: ground states of He I (1), of He II (30), and He III continuum (34). The population densities for these levels are divided by 108. Singlet excited levels represented: $\rm 1s2p~^1P$ (5, dashes) and $\rm 1s3d~^1D$ (10, long dashes). Triplet levels are: $\rm 1s2p~^3P$ (4, dots) and $\rm 1s3d~^3D$ (9, long dashes/dots). Level 31 is the n=2 level of He II (short dashes/dots).

5.2 Singlet lines: E(6678) and E(584)

The relation between the optically thin He I $\lambda$6678 Å and the optically thick resonance line He I $\lambda$584 Å is represented in Fig. 17. These two lines have a common level $\rm 1s2p~^1P$ which is the lower level of the 6678 transition (see Fig. 2). We can see that at low temperatures the 584 line is completely saturated and is independent of the model parameters (see Sect. 4.2) while the pressure variations decrease the 6678 line intensity. At a given temperature the line ratio depends on the pressure: an increase in the pressure leads to an increase of E(6678)/E(584). This is particularly true at high temperatures where the collisional excitation plays an important role in the 584 line wing emission.

   
5.3 Singlet and triplet lines: E(6678) and E(D3)

 

 

Table 6: He I triplet line ratios for 40 models with W=1000 km.

$E(10\,830)/E({\rm D}3)$	5.0
$E({\rm D}3)/E(7065)$	7.5
$E({\rm D}3)/E(3889)$	6.9
$E({\rm D}3)/E(3188)$	20.6
$E({\rm D}3)/E(4471)$	7.5

The relation between optically thin singlet and triplet lines is not as simple as for the triplet-triplet case. We have in this case to consider how the helium statistical equilibrium is reached for the whole atom. In the singlet system the presence of the resonance lines provides an efficient way to deexcite the $\rm 1snp~^1P$ states by spontaneous emission. In the triplet system the $\rm 1s2s~^3S$ metastable level acts as a ground state. The intersystem collisions tend to drive the electrons from triplet to singlet states. Moreover we have already noticed in Sect. 4 the weakness of the singlet lines relative to the triplet lines. Figure 18 illustrates the pressure dependance of the relation between the singlet $He {\sc i}~\lambda\,6678$ Å line integrated intensity and its triplet equivalent D3 line intensity. At low pressures (0.02 dyn/cm²) the relation between the two lines is almost linear. Landman & Illing (1976) have found a similarly linear relation between the two lines for one observed prominence (see their Fig. 3). The observed range of intensities was smaller than that represented in our Fig. 18: the D3 maximum intensity was less than $3 \times 10^3$ erg s^-1 cm^-2 sr^-1, and the maximum 6678 intensity was about 50 erg s^-1 cm^-2 sr^-1. But we can see that if the pressure is higher the relation between the two lines is no longer linear at all. At 0.05 dyn/cm² the integrated intensities are almost constant whatever the temperature, giving a limit ratio. If we increase the pressure this same limit value for the line ratio will be found for the lower temperatures. In this situation the formation of the two lines is mainly due to the scattering of the incident radiation because of a high optical thickness in the incident continuum radiation. For high pressure, high temperature models, the same optical depth is reduced and collisional excitation becomes important: this gives an increasing ratio of the two lines with the temperature and the pressure.

5.4 E(He II$\lambda$304) and E(He I$\lambda$584)

Ionized helium is coupled to neutral helium in several different ways in our model atom. Radiative bound - free transitions (photoionization and collisional ionization) are allowed between all neutral helium states and the ground state of He II. The photoionization of the He I ground level plays an important role since it is the main way to populate the excited levels by recombinations (PR process) when the temperature is not high enough to produce significant collisional excitation from the ground level towards the triplet states.

The relation between He II $\lambda$304 Å and He I $\lambda$584 Å shown in Fig. 19 indicates a decreasing ratio E(304)/E(584) with the temperature: the 304 line intensity also grows with the temperature, but more slowly than the 584 line intensity. At high temperatures the 584 line emission increases with the pressure because of collisional excitation while the 304 line is saturated and is formed by scattering of the incident radiation. A decrease of the temperature increases the E(304)/E(584) ratio up to a limit value which corresponds to a situation where both lines are formed by the scattering of the incident radiation.

5.5 He I D3 and H$\beta$ lines

 

Figure 14: Half emergent line profiles for two different models: T=6000 K, P=0.02 dyn/cm2 and W=1000 km (four top panels); $T=18\,000$ K, P=0.2 dyn/cm2 and W=1000 km (four bottom panels). Solid line: $n_{\rm He}/n_{\rm H}=0.05$; short dashes: $n_{\rm He}/n_{\rm H}=0.10$; dots/dashes: $n_{\rm He}/n_{\rm H}=0.15$; long dots/dashes: $n_{\rm He}/n_{\rm H}=0.20$. Same units as in Fig. 5.

The intensity ratio between the helium D3 line and the hydrogen Balmer lines has been measured by several observers (Landman & Illing 1976, 1977; Landman et al. 1977; Stellmacher 1979; Stellmacher & Wiehr 1995, 1997; de Boer et al. 1998, for instance). Figure 20 shows the theoretical behaviour of the $E({\rm D}3)/E({\rm H}\beta )$ ratio with the different physical parameters already considered in this work. First we can see that this ratio decreases with the slab thickness. $E({\rm D}3)$ increases with the slab thickness (Fig. 6), but more slowly than the H$\beta$intensity. $E({\rm D}3)/E({\rm H}\beta )$ is not very sensitive to the temperature at low pressure. We can see that at a fixed temperature the increase of the pressure causes the ratio to decrease because of a decrease of the mean helium ionization ratio. For the highest pressures where the ionization is low the only way to observe a significant $E({\rm D}3)/E({\rm H}\beta )$ value is to have high temperatures. The evolution of the ratio with helium abundance reflects the evolution of the D3 intensity with $n_{{\rm He}}/n_{{\rm H}}$(see Fig. 15) but with a higher slope. An increase of a factor of 4 in helium abundance leads to an increase of a factor of 3 for the intensity ratio in the case of a low pressure, low temperature model ($\Diamond$ in Fig. 20, bottom right panel). This corresponds to a decrease of about 15% of the H$\beta$ intensity with the abundance increase.

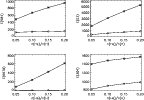Figure 15: Integrated intensities (in cgs units) for 4 lines as a function of the abundance computed for 2 models: T=6000 K, P=0.02 dyn/cm2 and W=1000 km ($\Diamond$); $T=18\,000$ K, P=0.2 dyn/cm2 and W=1000 km ($\ast$).

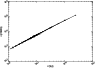Figure 16: $E(He {\sc i}~\lambda\,10\,830)$ versus $E({\rm D}3)$. Integrated intensities are in cgs units. Computations are made for 5 pressures and 8 temperatures. Same symbols as in Fig. 6.

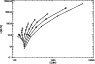Figure 17: $E(He {\sc i}~\lambda\,6678)$ versus $E(He {\sc i}~\lambda\,584)$ for 8 temperatures. Same symbols as in Fig. 6.

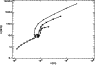Figure 18: $E(He {\sc i}~\lambda\,6678)$ versus $E({\rm D}3)$ for 5 pressures. Same symbols as in Fig. 9.

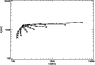Figure 19: $E(He {\sc ii}~\lambda\,304)$ versus $E(He {\sc i}~\lambda\,584)$ at 8 temperatures. Same symbols as in Fig. 6.

Heasley & Milkey (1976) have already discussed (see their Fig. 1) the theoretical behaviour of this relation relative to temperature, pressure, and column mass. If we increase the total column mass (increase of the H$\beta$ intensity) the prominence becomes optically thick in the Lyman continuum and the excitational and ionizing radiation penetrates less deeply in the slab, thus decreasing the ionization of helium. An increase in the pressure has the same effect: we obtain an increase of the recombination rates, thus reducing the helium ionization. Finally, a decrease in the temperature leads to a decrease of hydrogen and helium ionization (or an increase of the Lyman continuum optical thickness). We know that the recombination from the He II ground state is the main mechanism which populates the helium triplet states. This is consistent with the photoionization-recombination (PR) scheme which is believed to be the main population mechanism for helium in the solar atmosphere for temperatures below 20000 K (see e.g., Andretta & Jones 1997). These effects are also seen in our Fig. 3 (see Sect. 3.2). The tendancy of a lowering of the curve with increasing H$\beta$ intensities is also visible in the Fig. 6 of, e.g., de Boer et al. (1998). Our conclusion about helium excitation and ionization conditions are that as the hydrogen density increases, the $n_{He {\sc ii}}/n_{He {\sc i}}$ ratio decreases, but more rapidly at slab center where there is much less UV continuum radiation. This produces a too weak ionization at slab center to populate helium triplet states.

Figure 20: $E({\rm D}3)/E({\rm H}\beta )$ as a function of: the slab width (top left panel) at 8 temperatures (same symbols as in Fig. 6); the temperature (top right panel) at 5 pressures (same symbols as in Fig. 9); the pressure (bottom left panel) at 8 temperatures (same symbols as in Fig. 6); and the helium abundance (bottom right panel) for 2 models (same symbols as in Fig. 15).