

Up: Formation of helium spectrum
Subsections
4 Effect of physical parameters on helium states mean populations and on
emergent intensities
Table 4:
Physical parameters adopted for the grid of 480 different prominence
models.
| Parameter |
Value |
Unit |
| Temperature |
6000, 8000, 10000, 12000, |
|
| |
14000, 16000, 18000, 20000 |
K |
| Pressure |
0.02, 0.05, 0.10, 0.20, 0.50 |
dyn/cm2 |
| Slab width |
200, 1000, 5000 |
km |
| Microturbulent |
|
|
| velocity |
5 |
km s-1 |
| Altitude |
10000 |
km |
| He abundance |
|
|
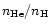 |
0.05, 0.10, 0.15, 0.20 |
|
We have performed numerical calculations for both hydrogen and helium spectra
for 480 models described in Table 4. In this section we show how the
mean population densities of helium vary with the physical parameters of the
prominence plasma. Mean populations are calculated following the formula:
where ni(z) is the population of level i at the depth z in the slab, and
W is the slab width. We focus our attention on 5 neutral helium levels
(
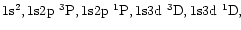 labelled 1, 4, 5, 9, and 10 in
Figs. 4, 7 and 10), 2 ionized helium levels
(n=1 and 2, labelled 30 and 31) and the continuum level He++ (labelled 34). Their mean populations are represented in Figs. 4, 7, and 10. Note that for clarity on those plots the mean
populations of He I and He II ground states as well as the
He III ionization level mean population have been multiplied by a factor 10-8. The bound levels chosen are involved in the transitions that we will
particularly study in the following and in Sect. 5. We also
present the influence of the different physical parameters presented in Table 4 on the emergent line profiles (Figs. 5, 8,
and 11) and integrated intensities (Figs. 6, 9, and 12). The line profiles are for a normal emergent intensity
(line-of-sight perpendicular to the slab surface). No result is shown
concerning the influence of the microturbulent velocity and the height of the
line-of-sight, because those parameters were taken as constant in the present
study. We will more particularly consider four lines: He I
labelled 1, 4, 5, 9, and 10 in
Figs. 4, 7 and 10), 2 ionized helium levels
(n=1 and 2, labelled 30 and 31) and the continuum level He++ (labelled 34). Their mean populations are represented in Figs. 4, 7, and 10. Note that for clarity on those plots the mean
populations of He I and He II ground states as well as the
He III ionization level mean population have been multiplied by a factor 10-8. The bound levels chosen are involved in the transitions that we will
particularly study in the following and in Sect. 5. We also
present the influence of the different physical parameters presented in Table 4 on the emergent line profiles (Figs. 5, 8,
and 11) and integrated intensities (Figs. 6, 9, and 12). The line profiles are for a normal emergent intensity
(line-of-sight perpendicular to the slab surface). No result is shown
concerning the influence of the microturbulent velocity and the height of the
line-of-sight, because those parameters were taken as constant in the present
study. We will more particularly consider four lines: He I
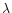 584 Å (optically thick resonance line between levels
584 Å (optically thick resonance line between levels 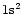 and
and
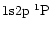 ), He I
), He I 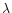 6678 Å (optically thin singlet line
between
6678 Å (optically thin singlet line
between
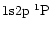 and
and
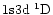 ), He I
), He I 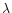 5876 Å (D3,
optically thin triplet line between
5876 Å (D3,
optically thin triplet line between
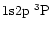 and
and
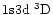 ), and
He II
), and
He II 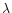 304 Å (optically thick resonance line). This will
give us an overview of the behaviour of the main helium spectral features in
quiescent prominences.
304 Å (optically thick resonance line). This will
give us an overview of the behaviour of the main helium spectral features in
quiescent prominences.
4.1 Influence of the slab width
 |
Figure 4:
Mean population densities (in cm-3) as a function of the slab
width (in km) for two different temperatures (6000 and 18000 K) and one
pressure (0.1 dyn/cm2). Solid lines: ground states of He I (1),
of He II (30), and He III continuum (34). The population
densities for these levels are divided by 108. Singlet
excited levels represented:
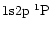 (5, dashes) and
(5, dashes) and
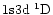 (10, long
dashes). Triplet levels are:
(10, long
dashes). Triplet levels are:
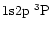 (4, dots) and
(4, dots) and
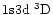 (9, long
dashes/dots). Level 31 is the n=2 level of He II (short dashes/dots).
(9, long
dashes/dots). Level 31 is the n=2 level of He II (short dashes/dots). |
![\begin{figure}
\par\resizebox{13cm}{!}{\includegraphics[clip]{MS1819f5A.ps}}\par\vspace*{2mm}
\resizebox{13cm}{!}{\includegraphics[clip]{MS1819f5B.ps}}\end{figure}](/articles/aa/full/2001/46/aa1819/Timg59.gif) |
Figure 5:
Half emergent line profiles for one pressure (0.1 dyn/cm2) at
6000 K (four top panels) and 18000 K (four bottom panels) for three
different slab widths. Solid line: W=200; dotted: W=1000; dashed:
W=5000 km. Intensities are in erg s-1 cm-2 sr-1 Å-1 (cgs units). |
![\begin{figure}
\par\resizebox{12.5cm}{!}{\includegraphics[clip]{MS1819f6.ps}}\end{figure}](/articles/aa/full/2001/46/aa1819/Timg60.gif) |
Figure 6:
Integrated intensities (in cgs units) for 4 lines as a function of the slab width W (in km) computed for one pressure (0.1 dyn/cm2) and 8 temperatures: 6000 K (no symbol), 8000 K ( ), 10000 K ( ), 10000 K ( ), 12000 K ( ), 12000 K ( ), 14000 K ( ), 14000 K ( ), 16000 K ( ), 16000 K ( ), 18000 K ( ), 18000 K ( ), and 20000 K (+). ), and 20000 K (+). |
We can see the influence of the slab width in Figs. 4 to 6.
At low temperatures the increase of the slab width tends to reduce the excited
mean populations while the ground state mean population is almost constant.
This is due to the fact that the ionizing radiation penetrates less deeply
towards the slab center as the width increases. As a consequence the optically
thick 584 line (which is mainly formed by the scattering of the incident
radiation at that wavelength) does not show any sensitivity to the slab width.
This is clearly seen in Fig. 5 (top panels) where we can see that
the line profile is not affected by the slab width variation. The optically
thick 304 line is also not affected by the width change. One can even note a
very slight decrease in the integrated intensity possibly due to continuous
absorption in the core of the slab. On the contrary the optically thin lines are
brighter when the slab width increases as a result of the increase of the
optical thickness and, consequently, of the scattering of the incident
radiation. However this brightening is not proportional to the width because
the excitation of the lower levels of the transitions also depends on the
penetration of the incident radiation in the resonance continuum at 504 Å:
the ionizing radiation penetrates less deeply as the slab width increases. This
effect is visible in Fig. 5: the brightening of the emergent
profile is larger when the slab width goes from 200 to 1000 km than between 1000 and 5000 km.
At high temperatures the situation is quite different.
The mean populations of He I ground state and singlet excited levels
increase with the slab width while the mean populations of triplet levels of
He I and He II decrease (Fig. 4, bottom panel). Again,
the helium ionization decreases at slab center as the width increases. The
triplet levels populations follow more or less the He II mean
populations since the dominant population mechanism for the triplet system is
the photoionization from the ground state of He I, followed by
recombinations to the triplet levels. This mechanism is known as the
photoionization - recombination (PR) process and is the dominant population
mechanism for helium below 20000 K (Andretta & Jones 1997). However we can see in Fig. 5 (bottom panels) that the collisional excitations play an important
role on the neutral helium lines formation. The optically thin lines are
brighter at line center as well as in the wings. The 304 line is saturated at
line center where only resonant scattering occurs but the wings are broadened
when the slab width increases. As the 584 line, it is also saturated at line
center but we observe an intensity peak between 0.05 and 0.06 Å from line
center due to collisional excitations. The total number of photons created by
collisional excitation increases with the slab width. We can also note that the
increase of the mean populations of neutral helium singlet levels with the slab width
at high temperature is due to intersystem (triplet to singlet states)
collisions. But in any case it is seen in Fig. 4 that the singlet
states are underpopulated relative to their triplet equivalent states (N5 <
N4 and
N10 < N9) whatever the temperature.
4.2 Influence of the temperature
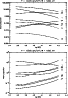 |
Figure 7:
Mean population densities (in cm-3) as a function of the
temperature (in K) for two different pressures (0.02 and 0.2 dyn/cm2) and
one slab width (1000 km). Solid lines: ground states of He I (1), of
He II (30), and He III continuum (34). The population densities
for these levels are divided by 108. Singlet excited levels
represented:
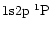 (5, dashes) and
(5, dashes) and
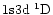 (10, long dashes). Triplet
levels are:
(10, long dashes). Triplet
levels are:
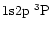 (4, dots) and
(4, dots) and
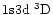 (9, long dashes/dots). Level 31
is the n=2 level of He II (short dashes/dots).
(9, long dashes/dots). Level 31
is the n=2 level of He II (short dashes/dots). |
The effect of the temperature on the mean populations and the emergent
intensities are shown in Figs. 7 to 9. At low pressures we
can see that an increase of the temperature reduces the neutral helium mean
population and raises the ionized helium population (top panel of Fig. 7). Moreover we note that at low pressures, for a temperature
greater than 11000 K (
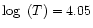 ), we get
), we get
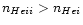 .
The small optical thickness (
.
The small optical thickness (
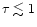 )
of the Lyman continuum of hydrogen and of the neutral helium continuum
favors the penetration of the EUV ionizing radiation. Since, at the same time,
the recombination rates are low, we obtain a high helium ionization. The 584
line profile (Fig. 8) shows an increase of thermal emission in the
line wings with the temperature, as the 304 line. At line center these
optically thick lines are saturated and scatter the radiation. On the contrary
the increase of temperature, which lowers the optical thickness, leads to a
decrease of the scattering for the optically thin lines and thus a decrease of
their emergent intensities (Fig. 9).
)
of the Lyman continuum of hydrogen and of the neutral helium continuum
favors the penetration of the EUV ionizing radiation. Since, at the same time,
the recombination rates are low, we obtain a high helium ionization. The 584
line profile (Fig. 8) shows an increase of thermal emission in the
line wings with the temperature, as the 304 line. At line center these
optically thick lines are saturated and scatter the radiation. On the contrary
the increase of temperature, which lowers the optical thickness, leads to a
decrease of the scattering for the optically thin lines and thus a decrease of
their emergent intensities (Fig. 9).
At high pressures all mean
populations increase with the temperature except that of the He I ground
state (bottom panel of Fig. 7). But now helium ionization is lower
(
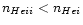 )
because of optical thickness of the
neutral helium continuum (
)
because of optical thickness of the
neutral helium continuum (
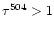 )
which prevents the EUV incident
radiation from reaching the core of the slab. The higher pressures also give
higher recombination rates. All emergent intensities grow with temperature
(Fig. 9). In Fig. 8 we see that in the 584 resonance line a
peak at about 0.05 Å from line center appears above 14000 K, and its
intensity increases with the temperature, while the line center is saturated.
At high pressures collisional excitation becomes more significant when the
temperature increases for this transition. For He II
)
which prevents the EUV incident
radiation from reaching the core of the slab. The higher pressures also give
higher recombination rates. All emergent intensities grow with temperature
(Fig. 9). In Fig. 8 we see that in the 584 resonance line a
peak at about 0.05 Å from line center appears above 14000 K, and its
intensity increases with the temperature, while the line center is saturated.
At high pressures collisional excitation becomes more significant when the
temperature increases for this transition. For He II 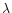 304 Å the line center saturation is less pronounced than at low pressures but the
temperature rise mostly broadens the profile. The 304 emitted intensity is
not very sensitive to the temperature (Fig. 9), probably because the
considered temperatures lie well below the excitation temperature of this
line. From He II
304 Å the line center saturation is less pronounced than at low pressures but the
temperature rise mostly broadens the profile. The 304 emitted intensity is
not very sensitive to the temperature (Fig. 9), probably because the
considered temperatures lie well below the excitation temperature of this
line. From He II 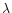 1640 Å line profiles observed with Skylab
in a prominence, Mariska et al. (1979) derived an average temperature of
27000 K for the region where He II is emitted. Our computed models
have temperatures below 20000 K and the collisional processes are likely of
secondary importance relative to the scattering of the incident radiation for
the 304 line. Finally the optically thin lines at high pressures are mostly
affected by thermal processes which enhances the line intensity as the
temperature increases.
1640 Å line profiles observed with Skylab
in a prominence, Mariska et al. (1979) derived an average temperature of
27000 K for the region where He II is emitted. Our computed models
have temperatures below 20000 K and the collisional processes are likely of
secondary importance relative to the scattering of the incident radiation for
the 304 line. Finally the optically thin lines at high pressures are mostly
affected by thermal processes which enhances the line intensity as the
temperature increases.
4.3 Influence of the gas pressure
The evolution of the mean populations, emergent line profiles and integrated
intensities with the pressure can be seen in Figs. 10 to 12.
At low temperatures the He II and He III mean populations
decrease with the pressure while a large increase occurs for the He I
ground state population (Fig. 10, top panel). The populations of the
excited singlet and triplet levels are roughly constant. The increase of the
pressure raises the optical depth in the ionization continuum. Thus the helium
ionization ratio decreases with pressure. Looking at the emergent profiles
(Fig. 11) confirms this: the 584 line only scatters the incident
radiation because of its large optical thickness and the pressure increase has
almost no influence on the profile shape. Due to the large decrease of the
ionization ratio and the increase of the continuum optical depth, the 304 line
intensity is reduced. The increase in pressure produces an increase in
collisional excitation in the optically thin lines.
At higher temperatures
all neutral helium states see their mean populations increasing with
pressure (bottom panel of Fig. 10). This is also the case for the
He II populations but less markedly. He III mean population
decreases with the pressure. At those high temperatures the optical depth at
912 Å is less than unity. The helium ionization ratio in this case is
larger than at low temperatures and recombination becomes more efficient as
the pressure increases to populate the neutral helium excited levels. Moreover
the 504 He I continuum becomes optically thick as the pressure increases
and thus decreases the
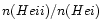 and the
and the
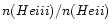 ratios. The optically thin line profiles
show the same characteristics than at low temperature (see Fig. 11)
but at high temperatures the collisional excitation enhances the line
intensity. The 584 line also shows the importance of collisional excitation
with a brightening in the wing giving an emission peak at about 0.05 Å
while line center is still saturated and only permits scattering of the
incident radiation. At those high temperatures, collisional processes become
non negligible in the formation of the line relative to the scattering of the
incident radiation. This is obviously not the case for the 304 line where no
intensity increase is observed (see also Fig. 12). As previously
stated, the temperatures under consideration are not high enough to see any
effect of collisional processes in the formation of the line and we only
observe scattering of radiation.
ratios. The optically thin line profiles
show the same characteristics than at low temperature (see Fig. 11)
but at high temperatures the collisional excitation enhances the line
intensity. The 584 line also shows the importance of collisional excitation
with a brightening in the wing giving an emission peak at about 0.05 Å
while line center is still saturated and only permits scattering of the
incident radiation. At those high temperatures, collisional processes become
non negligible in the formation of the line relative to the scattering of the
incident radiation. This is obviously not the case for the 304 line where no
intensity increase is observed (see also Fig. 12). As previously
stated, the temperatures under consideration are not high enough to see any
effect of collisional processes in the formation of the line and we only
observe scattering of radiation.
![\begin{figure}
\par\resizebox{13cm}{!}{\includegraphics[clip]{MS1819f8A.ps}}\par\vspace*{2mm}
\resizebox{13cm}{!}{\includegraphics[clip]{MS1819f8B.ps}}\end{figure}](/articles/aa/full/2001/46/aa1819/Timg69.gif) |
Figure 8:
Half emergent line profiles for one slab width (1000 km) at 0.02 dyn/cm2 (four top panels) and 0.2 dyn/cm2 (four bottom panels). The increase of line thickness corresponds to an increase of temperature. The different temperatures are 6000, 8000, 10000, 12000, 14000, 16000, 18000, and 20000 K. Same units as in Fig. 5. |
![\begin{figure}
\par\resizebox{12cm}{!}{\includegraphics[clip]{MS1819f9.ps}} %
\end{figure}](/articles/aa/full/2001/46/aa1819/Timg70.gif) |
Figure 9:
Integrated intensities (in cgs units) for 4 lines as a function of the temperature computed for one slab width (1000 km) and five pressures: 0.02 ( ), 0.05 ( ), 0.05 (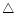 ), 0.1 ( ), 0.1 ( ), 0.2 ( ), 0.2 ( ), and 0.5 dyn/cm2 (+). ), and 0.5 dyn/cm2 (+). |
 |
Figure 10:
Mean population densities (in cm-3) as a function of the pressure
(in dyn/cm2) for two different temperatures (6000 and 18000 K) and one
slab width (1000 km). Solid lines: ground states of He I (1), of
He II (30), and He III continuum (34). The population densities
for these levels are divided by 108. Singlet excited levels
represented:
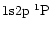 (5, dashes) and
(5, dashes) and
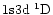 (10, long dashes). Triplet
levels are:
(10, long dashes). Triplet
levels are:
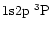 (4, dots) and
(4, dots) and
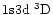 (9, long dashes/dots). Level 31 is the n=2 level of He II (short dashes/dots).
(9, long dashes/dots). Level 31 is the n=2 level of He II (short dashes/dots). |
The helium abundance is a long-standing issue in the solar atmosphere as well
as in prominences. Many authors have tried to determine the abundance from
prominence observations and HM3 have used their modelling of
H I, He I and Ca II lines to infer a helium-to-hydrogen
ratio of
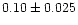 .
Lower ratios have been proposed by
Yakovkin et al. (1982). These authors inferred a helium abundance close to 0.05 from
a solution of the integral diffusion equations. However they only computed
low-temperature models (
.
Lower ratios have been proposed by
Yakovkin et al. (1982). These authors inferred a helium abundance close to 0.05 from
a solution of the integral diffusion equations. However they only computed
low-temperature models (
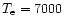 K) that do not take into consideration
the presence at the prominence edges of hotter plasma. Hirayama (1971) found
0.065 with the assumption that both hydrogen and helium are fully ionized in
the emitting region, an assumption that is unrealistic. In this paper we present
theoretical calculations with a helium abundance of 0.10 by number relative to
hydrogen. Nevertheless in this section we want to explore as a first step the
influence of the helium abundance on mean populations, line profiles and
integrated intensities. For the sake of simplicity we have chosen only two
different models corresponding to different physical conditions in the
prominence: model 6, with T=6000 K, P=0.02 dyn/cm2 and W=1000 km, and model 99, with
K) that do not take into consideration
the presence at the prominence edges of hotter plasma. Hirayama (1971) found
0.065 with the assumption that both hydrogen and helium are fully ionized in
the emitting region, an assumption that is unrealistic. In this paper we present
theoretical calculations with a helium abundance of 0.10 by number relative to
hydrogen. Nevertheless in this section we want to explore as a first step the
influence of the helium abundance on mean populations, line profiles and
integrated intensities. For the sake of simplicity we have chosen only two
different models corresponding to different physical conditions in the
prominence: model 6, with T=6000 K, P=0.02 dyn/cm2 and W=1000 km, and model 99, with 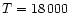 K, P=0.2 dyn/cm2 and W=1000 km.
These two models are referenced in Table 5 and the hydrogen
and electron mean population as well as the optical depths at the head of the
different continua are given for each of the four abundances considered. The
variation of helium mean populations, emergent profiles and integrated
intensities with the helium abundance are represented in Figs. 13 to 15.
K, P=0.2 dyn/cm2 and W=1000 km.
These two models are referenced in Table 5 and the hydrogen
and electron mean population as well as the optical depths at the head of the
different continua are given for each of the four abundances considered. The
variation of helium mean populations, emergent profiles and integrated
intensities with the helium abundance are represented in Figs. 13 to 15.
For the low temperature, low pressure model, the influence of
the helium abundance is clearly visible on the neutral singlet states (Fig. 13, top panel). The excited singlet states mean populations are
particularly enhanced with the abundance increase (by a factor greater than 6
as for the level 5). The triplet states and He II populations are less
affected by the abundance. We can see from Table 5 that the
increase of the He I ground state population leads to an optically thick
resonance continuum, and this gives a decrease of the helium ionization with
abundance. Thus the increase of abundance affects the population mechanism of
neutral helium because of the increase of the optical depth at 504 Å (and
also a decrease of the optical depth at 912 Å). The optically thick lines
are saturated and the 584 line emergent profile is slightly broadened by the
abundance increase (optical depth effect), while the 304 line profile does not
show any variation. The resulting integrated intensities are almost constant
(Fig. 15 and four top panels of Fig. 14). The optically
thin line profiles see their line center and line wings intensities enhanced by
the abundance increase. The 6678 singlet line is the most affected: its
integrated intensity is enhanced by a factor greater than 5 while the triplet D3 line integrated intensity is increased by a factor of less than 3. These
intensity enhancements for the optically thin lines with the helium abundance
correspond to the increase of the upper state mean population of the related
transition. The increase of the singlet-to-triplet line ratio with abundance is
due to the fact that the optical depth of the 584 line grows with helium
abundance. Thus, the emission of photons from the excited singlet states will
be preferably through the optically thin lines (such as the 6678 line) rather
than the resonance lines. In the triplet system the abundance effect is limited
by the presence of the metastable level
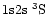 .
.
For the high
temperature, high pressure model, the evolution of the mean population
densities is similar to the low temperature, low pressure case, but the excited
states population increase is larger in this case (Fig. 13).
Again, we observe a decrease of the helium ionization due to the increase of
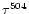 .
The increase of He abundance also raises the singlet-to-triplet
line ratios (Fig. 15). The optically thin line profiles show the same
evolution with abundance and again, there is a larger increase with abundance
(of a factor more than 7) in the integrated intensity of the 6678 line than
for the triplet line. The 304 line formation is still dominated by the
scattering of the incident radiation (Fig. 14) and its integrated
intensity is constant with the abundance variation. Finally, the 584 line
exhibits a peak around 0.055 Å from line center due to collisional
excitation from the ground state. The height of this peak and its distance from
the line center are increasing with the abundance.
.
The increase of He abundance also raises the singlet-to-triplet
line ratios (Fig. 15). The optically thin line profiles show the same
evolution with abundance and again, there is a larger increase with abundance
(of a factor more than 7) in the integrated intensity of the 6678 line than
for the triplet line. The 304 line formation is still dominated by the
scattering of the incident radiation (Fig. 14) and its integrated
intensity is constant with the abundance variation. Finally, the 584 line
exhibits a peak around 0.055 Å from line center due to collisional
excitation from the ground state. The height of this peak and its distance from
the line center are increasing with the abundance.
From this study we see
that the different sensitivities of line intensities (optically thick vs.
optically thin, singlet vs. triplet) could be used, as well as the comparison
with hydrogen lines, to improve the diagnostics of helium abundance in
prominences.


Up: Formation of helium spectrum
Copyright ESO 2001
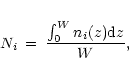

![\begin{figure}
\par\resizebox{13cm}{!}{\includegraphics[clip]{MS1819f5A.ps}}\par\vspace*{2mm}
\resizebox{13cm}{!}{\includegraphics[clip]{MS1819f5B.ps}}\end{figure}](/articles/aa/full/2001/46/aa1819/Timg59.gif)
![\begin{figure}
\par\resizebox{12.5cm}{!}{\includegraphics[clip]{MS1819f6.ps}}\end{figure}](/articles/aa/full/2001/46/aa1819/Timg60.gif)

![\begin{figure}
\par\resizebox{13cm}{!}{\includegraphics[clip]{MS1819f8A.ps}}\par\vspace*{2mm}
\resizebox{13cm}{!}{\includegraphics[clip]{MS1819f8B.ps}}\end{figure}](/articles/aa/full/2001/46/aa1819/Timg69.gif)
![\begin{figure}
\par\resizebox{12cm}{!}{\includegraphics[clip]{MS1819f9.ps}} %
\end{figure}](/articles/aa/full/2001/46/aa1819/Timg70.gif)
