

Up: Formation of helium spectrum
Subsections
3 Comparisons with previous theoretical works
Table 1:
Comparisons between modelling parameters for Heasley and co-workers and this work.
| |
hydrogen |
helium |
| |
Heasley et al. |
here |
Heasley et al. |
here |
| Number of levels |
5+1 (HMP, HM2) |
20+1 |
15+4+1 |
29+4+1 |
| in the model atom |
35+1 (HM3) |
|
|
|
| Frequency redistribution |
|
|
|
|
| in resonance lines |
complete (CRD) |
partial (PRD) |
complete (CRD) |
partial (PRD) |
| Detailed balance |
Lyman lines |
Lyman lines with 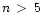 |
resonance lines |
no |
| Detailed incident profile |
no |
10 lines with upper level 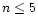 |
no |
2 lines (584 Å, 304 Å) |
It is interesting to compare our results to the pionnering work done by Heasley
and his colleagues. We again emphasize that we have removed some restrictive
simplifications that were made in their calculations such as the complete
redistribution in frequency (CRD). Partial frequency redistribution (PRD) is
considered in our calculations for the two first hydrogen Lyman lines and for
He I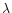 584 Å and He II
584 Å and He II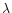 304 Å. In
addition, we use frequency-dependent incident line profiles for the principal
transitions (see Table 1). Heinzel et al. (1987) have shown that in the
case of hydrogen the combined use of these detailed incident profiles with PRD
may change drastically the emitted profiles.
304 Å. In
addition, we use frequency-dependent incident line profiles for the principal
transitions (see Table 1). Heinzel et al. (1987) have shown that in the
case of hydrogen the combined use of these detailed incident profiles with PRD
may change drastically the emitted profiles.
Table 3:
Comparison of optical properties (HMP models). Integrated helium line
intensities (ergs cm-2 s-1 sr-1).
| |
|
|
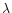 (Å)
(Å) |
| Model |
T |
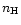 |
304 |
537 |
584 |
3889 |
5876 |
6678 |
7065 |
10830 |
| HMP 1 |
6000 |
1010 |
341 |
8 |
356 |
235 |
1844 |
61 |
222 |
8438 |
| here |
|
|
906 |
5 |
134 |
170 |
1300 |
21 |
164 |
6190 |
| HMP 3 |
6000 |
1012 |
132 |
4 |
54 |
73 |
567 |
6 |
69 |
2625 |
| here |
|
|
414 |
5 |
117 |
86 |
661 |
12 |
83 |
3140 |
| HMP 7 |
8000 |
1010 |
424 |
9 |
370 |
259 |
2032 |
61 |
245 |
9300 |
| here |
|
|
1100 |
6 |
154 |
197 |
1500 |
26 |
190 |
7160 |
| HMP 9 |
8000 |
1012 |
150 |
4 |
65 |
102 |
784 |
9 |
95 |
3615 |
| here |
|
|
431 |
6 |
134 |
60 |
449 |
20 |
56 |
2110 |
The first paper of the series (HMP) considers hydrogen and helium
(neutral and ionized) spectra emitted by the same geometrical prominence model
as described above. The dilution factor for all lines and continua is taken to
be
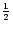 ,
corresponding to a zero altitude. They use a 15+4+1 helium
atom. Levels for He I with quantum number n=4 and n=5 are included
as grouped L states, keeping the distinction between singlet and triplet
states. Collisional rates are given by Mihalas & Stone (1968), and Auer & Mihalas (1973) give
collisional rates not included in Mihalas & Stone (1968) as well as photoionization
rates. Oscillator strengths are obtained from Wiese et al. (1966). No turbulent
broadening is considered, and CRD is assumed. HMP have adopted a
relation which defines the radiation temperature as a function of wavelength
for the incident radiation for continuum points (see their Fig. 1). But their
relation was inaccurate for the continuum incident radiation shortward of 304 Å. They indeed extrapolated EUV fluxes for the He II resonance
continuum from OSO-4 and OSO-6 spectrometers which had a wavelength cutoff at
about 300 Å. In all our calculations we therefore use EUV fluxes given by
Heroux et al. (1974) that give more ionizing radiation in the He II
resonance continuum. No emergent profile is shown in their paper.
Table 1 lists the main differences between their computations and
our code.
,
corresponding to a zero altitude. They use a 15+4+1 helium
atom. Levels for He I with quantum number n=4 and n=5 are included
as grouped L states, keeping the distinction between singlet and triplet
states. Collisional rates are given by Mihalas & Stone (1968), and Auer & Mihalas (1973) give
collisional rates not included in Mihalas & Stone (1968) as well as photoionization
rates. Oscillator strengths are obtained from Wiese et al. (1966). No turbulent
broadening is considered, and CRD is assumed. HMP have adopted a
relation which defines the radiation temperature as a function of wavelength
for the incident radiation for continuum points (see their Fig. 1). But their
relation was inaccurate for the continuum incident radiation shortward of 304 Å. They indeed extrapolated EUV fluxes for the He II resonance
continuum from OSO-4 and OSO-6 spectrometers which had a wavelength cutoff at
about 300 Å. In all our calculations we therefore use EUV fluxes given by
Heroux et al. (1974) that give more ionizing radiation in the He II
resonance continuum. No emergent profile is shown in their paper.
Table 1 lists the main differences between their computations and
our code.
We indicate in Tables 2 and 3 some
comparisons for four computed models, which all have a slab thickness of 6000
km at height H=0 km, temperatures of 6000 (models HMP 1 and 3) and 8000 K
(models HMP 7 and 9), and mean hydrogen densities of 1010 (models HMP 1
and 7) and 1012 cm-3 (models HMP 3 and 9). Table 2
presents the comparisons for the optical depths at the head of the Lyman
continuum (
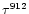 ), of the He I continuum (
), of the He I continuum (
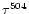 ), of the
He II continuum (
), of the
He II continuum (
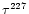 ), and at the 584 line center
(
), and at the 584 line center
(
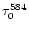 ), as well as the population ratios
), as well as the population ratios
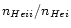 and
and
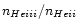 .
Table 3 shows the results for the integrated intensities of the
He II
.
Table 3 shows the results for the integrated intensities of the
He II 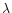 304 Å line and several neutral helium lines.
304 Å line and several neutral helium lines.
One
can note a rather good agreement between the two computations, except for the
population ratios
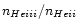 and
and
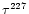 .
At
high densities a large disagreement occurs for those quantities. This
discrepancy is mainly due to the different incident continuum radiation in the
He II resonance continuum. We have an ionization continuum which is much
more efficient to populate He III. Examination of
.
At
high densities a large disagreement occurs for those quantities. This
discrepancy is mainly due to the different incident continuum radiation in the
He II resonance continuum. We have an ionization continuum which is much
more efficient to populate He III. Examination of
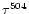 and
and
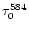 indicates that the neutral helium populations are of the same
order in both works. At low densities we have less He II and more
He III than HMP. The increase of pressure leads to lower
indicates that the neutral helium populations are of the same
order in both works. At low densities we have less He II and more
He III than HMP. The increase of pressure leads to lower
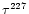 in
our computations but has the opposite effect in HMP calculations. This implies
that the penetration of the EUV ionizing radiation is much more effective for
our models. The result is that we get a much larger He III population in
the slab. The integrated intensities in Table 3 reflect this
situation. The neutral helium line intensities are roughly of the same order in
HMP calculations and ours, but the He II
in
our computations but has the opposite effect in HMP calculations. This implies
that the penetration of the EUV ionizing radiation is much more effective for
our models. The result is that we get a much larger He III population in
the slab. The integrated intensities in Table 3 reflect this
situation. The neutral helium line intensities are roughly of the same order in
HMP calculations and ours, but the He II 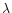 304 Å line
intensity is systematically higher in our computations. At those high pressures
fast recombinations from the He III ionization level follow the
photoionization of the He II ground state. Radiative cascades towards
the ground level of He II then occur, thus producing a strong emission
in the 304 resonance line. Nevertheless the high densities of HMP models imply
high pressures of about 1 dyn/cm2 and more which should not be regarded as
very representative of the actual pressures in quiescent prominences.
304 Å line
intensity is systematically higher in our computations. At those high pressures
fast recombinations from the He III ionization level follow the
photoionization of the He II ground state. Radiative cascades towards
the ground level of He II then occur, thus producing a strong emission
in the 304 resonance line. Nevertheless the high densities of HMP models imply
high pressures of about 1 dyn/cm2 and more which should not be regarded as
very representative of the actual pressures in quiescent prominences.
3.2 Heasley & Milkey (1978)
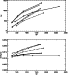 |
Figure 3:
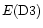 (top) and
(top) and
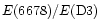 (bottom) versus
(bottom) versus
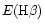 for 3 models of HM3. Dashed lines are calculations by HM3, and solid lines represent our results. The three kinds of models are: 7500, 0.01 (+); 9000, 0.015 (
for 3 models of HM3. Dashed lines are calculations by HM3, and solid lines represent our results. The three kinds of models are: 7500, 0.01 (+); 9000, 0.015 ( ); 7500, 0.02 ( ); 7500, 0.02 ( ). Integrated intensities are in cgs units. ). Integrated intensities are in cgs units. |
HM3 presented new computations of hydrogen and helium
emerging spectra for more realistic models with more realistic temperature and
pressure values as compared to HMP, new continuum incident
intensities of Heroux et al. (1974), and lower dilution factors for the incident
radiation. This was necessary for the authors in order to match the prominence
observations made available by Landman & Illing (1977). Unfortunately they do not give the
new dilution factors that they adopted. We therefore use a dilution factor
corresponding to an altitude of 10000 km, viz. 0.416 (if there is no
center-to-limb effect). CRD is still assumed for all lines and continua.
Moreover they have solved the statistical equilibrium equations with the
assumption that all Lyman lines are in detailed radiative balance. No emergent
profiles and no quantities related to He II are given.
HM3 studied the triplet line D3 and the 6678/D3 singlet-triplet
line ratio. Figure 3 presents comparisons between HM3
results and our computations for
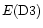 and
and
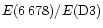 versus
versus
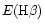 for three classes of
models without microturbulent velocity and defined by the temperature and the
pressure: (7500, 0.01); (9000, 0.015); (7500, 0.02) - see their
Figs. 4 to 6. In each model different calculations were made for column
masses of
for three classes of
models without microturbulent velocity and defined by the temperature and the
pressure: (7500, 0.01); (9000, 0.015); (7500, 0.02) - see their
Figs. 4 to 6. In each model different calculations were made for column
masses of
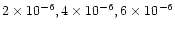 ,
and
,
and
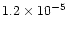 g/cm2. We can notice that our
g/cm2. We can notice that our
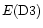 are larger in
every case than those of HM3. This seems to be due to a better
penetration of the ionizing incident radiation in our models since helium
recombination tends to populate the triplet levels. We also recall the
uncertainty in the dilution factors that they used for the incident radiation.
The relation between
are larger in
every case than those of HM3. This seems to be due to a better
penetration of the ionizing incident radiation in our models since helium
recombination tends to populate the triplet levels. We also recall the
uncertainty in the dilution factors that they used for the incident radiation.
The relation between
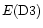 and
and
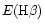 is studied in
Sect. 5.5 for a larger number of models. On the other hand the ratio
is studied in
Sect. 5.5 for a larger number of models. On the other hand the ratio
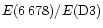 is lower in our computations than in
HM3. Again the better penetration of the incident continuum
explains this situation since ionization of helium hardly affects the singlet
states populations but populates the triplet states through recombination.
Moreover, the ratio
is lower in our computations than in
HM3. Again the better penetration of the incident continuum
explains this situation since ionization of helium hardly affects the singlet
states populations but populates the triplet states through recombination.
Moreover, the ratio
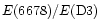 varies much less in our
computations, especially for the (7500, 0.02) models. It indicates that
the line formation processes for both the D3 and the 6678 lines are not
altered with the increase of the H
varies much less in our
computations, especially for the (7500, 0.02) models. It indicates that
the line formation processes for both the D3 and the 6678 lines are not
altered with the increase of the H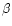 intensity, or in other words they
do not change much with the increase of hydrogen column mass in this domain of temperatures and pressures. The main contribution in the line formation comes from the scattering of the incident radiation. Of course, absolute intensities
increase with the hydrogen column mass. We will see in Sect. 5.3 (Fig. 18) that the relation between E(6678) and
intensity, or in other words they
do not change much with the increase of hydrogen column mass in this domain of temperatures and pressures. The main contribution in the line formation comes from the scattering of the incident radiation. Of course, absolute intensities
increase with the hydrogen column mass. We will see in Sect. 5.3 (Fig. 18) that the relation between E(6678) and
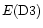 strongly depends on the temperature and the pressure.
strongly depends on the temperature and the pressure.


Up: Formation of helium spectrum
Copyright ESO 2001
