

Up: Formation of helium spectrum
Subsections
2 Modelling
The first step in our calculations is to solve the ionization, hydrostatic and
statistical equilibrium equations as well as the radiative transfer equations
out of local thermodynamic equilibrium (non LTE) for hydrogen. Computational
details can be found in Gouttebroze et al. (1993, hereafter GHV). We obtain electron and
hydrogen level population densities from which we can determine the hydrogen
spectrum emitted by our prominence. We thus derive the radiation inside the
slab, taking into account the incident radiation and the principal transitions
of the hydrogen atom. This defines the new physical conditions for the
computation of the helium spectrum. The second step is then to solve
independently the statistical equilibrium and the radiative transfer equations
for the multilevel, multi-ion helium atom. The solution of the statistical
equilibrium equations is determined by iterations and the radiative transfer
equations are solved by the Feautrier method (finite-difference method,
Feautrier 1964) with variable Eddington factors (Auer & Mihalas 1970). In all
calculations, partial redistribution in frequency is considered for the
formation of the resonance lines H I Ly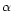 and Ly
and Ly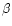 (Heinzel et al. 1987), He I
(Heinzel et al. 1987), He I 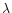 584 Å and He II
584 Å and He II 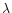 304 Å.
304 Å.
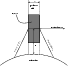 |
Figure 1:
Prominence model. T, P, and V are respectively the electron
temperature, the gas pressure, and the microturbulent velocity. H is the
height of observation above the solar surface and W the slab geometrical
thickness. |
The prominence model used here is the same as described in GHV -
see also Heinzel et al. (1987, 1994). It consists of a plane, parallel slab standing
vertically above the solar surface (see Fig. 1). It is a
one-dimensional representation defined by the slab thickness W. On both sides
of this symmetric model, the prominence is illuminated by an incident radiation
field coming from the underlying photosphere and chromosphere, and the
surrounding corona. This radiation field determines the boundary conditions for
the resolution of the radiative transfer equations and it is crucial to
consider it properly in order to study line formation. This radiation field is diluted
according to the height H of the line-of-sight above the solar surface and
eventually to the center-to-limb variations for the incident lines. In our computations the
center-to-limb variations are taken into account for the incident hydrogen
lines with upper level 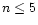 (Gouttebroze & Labrosse 2000). The emerging
spectrum is computed for three viewing angles:
(Gouttebroze & Labrosse 2000). The emerging
spectrum is computed for three viewing angles:
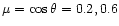 and 1. This last value corresponds to a line-of-sight perpendicular to the
slab and will be the only one considered in this paper, for brevity. Inside the slab, three physical quantities have to be defined: the
electron temperature, the gas pressure and the microturbulent velocity. In this
work we use isobaric and isothermal models, so these three quantities are
fixed constant throughout the slab. Consequently, each model is defined by 5 parameters, namely the electron temperature, the gas pressure, the
microturbulent velocity, the slab thickness and the height above the solar surface.
and 1. This last value corresponds to a line-of-sight perpendicular to the
slab and will be the only one considered in this paper, for brevity. Inside the slab, three physical quantities have to be defined: the
electron temperature, the gas pressure and the microturbulent velocity. In this
work we use isobaric and isothermal models, so these three quantities are
fixed constant throughout the slab. Consequently, each model is defined by 5 parameters, namely the electron temperature, the gas pressure, the
microturbulent velocity, the slab thickness and the height above the solar surface.
Numerical codes for the hydrogen emerging spectrum from a quiescent
prominence can be found on the MEDOC web
site![[*]](/icons/foot_motif.gif) (Gouttebroze & Labrosse 2000).
(Gouttebroze & Labrosse 2000).
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[scale=0.5]{MS1819f2.ps}}\end{figure}](/articles/aa/full/2001/46/aa1819/Timg38.gif) |
Figure 2:
Diagram of the neutral helium energy levels. The energy scale has been
shortened between 0 and 20 eV. We indicate for the 11 first states the index of the level with
increasing energy relative to the ground state. Solid lines represent some of
the transitions often observed in quiescent prominences, and the dashed line
represents the ionization continuum at 504 Å. |
We use very detailed atomic models for both hydrogen and helium. The hydrogen
atom is the same as in GHV (20 bound levels plus continuum).
For neutral helium we use the atomic model of Benjamin et al. (1999 hereafter
BSS). Thus we consider in our calculations 29 energy levels up to n=5,
divided into individual (L,S) states, which allows us to keep the distinction
between singlet (S=0) and triplet (S=1) levels. Energy levels and
statistical weights are given by Wiese et al. (1966). It is important to have this
distinction in the model atom between neutral helium singlet and triplet levels
because they are not populated through the same processes. Figure
2 represents schematically the neutral helium states included
in the calculations up to n = 5. Note that the energy scale has been modified
in order to lessen the large gap between the ground state 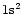 and the first
excited level
and the first
excited level
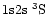 .
The latter is a metastable state and is the lower
state of the infrared He I
.
The latter is a metastable state and is the lower
state of the infrared He I  10830 Å line. In Fig. 2 we show some line transitions which will be the
subject of further investigations in Sects. 4 and 5, as well as the resonance continuum transition which
occurs at 504 Å. The optically thick resonance lines lie in the singlet
system. There are no permitted radiative transitions between the two systems,
but they are coupled through collisions. Effective collision strengths,
collisional ionization coefficients and spontaneous emission coefficients are
from BSS. Collisions strengths not defined in BSS
are taken in Benson & Kulander (1972). Coefficients for Stark broadening are from
Dimitrijevic & Sahal-Brechot (1984), and from Griem (1974) for transitions not defined in
Dimitrijevic & Sahal-Brechot. Photoionization cross sections are from TOPBASE
(Fernley et al. 1987).
10830 Å line. In Fig. 2 we show some line transitions which will be the
subject of further investigations in Sects. 4 and 5, as well as the resonance continuum transition which
occurs at 504 Å. The optically thick resonance lines lie in the singlet
system. There are no permitted radiative transitions between the two systems,
but they are coupled through collisions. Effective collision strengths,
collisional ionization coefficients and spontaneous emission coefficients are
from BSS. Collisions strengths not defined in BSS
are taken in Benson & Kulander (1972). Coefficients for Stark broadening are from
Dimitrijevic & Sahal-Brechot (1984), and from Griem (1974) for transitions not defined in
Dimitrijevic & Sahal-Brechot. Photoionization cross sections are from TOPBASE
(Fernley et al. 1987).
For ionized helium we use a simple 4 bound levels
atomic model. Energy levels and statistical weights again are given by
Wiese et al. (1966). Effective collision strengths are from Aggarwal et al. (1992)
for collisional transitions up to n=3 and from Aggarwal et al. (1991) for
transitions up to n=4. Collisional ionization coefficients are calculated as
in Mihalas & Stone (1968). Spontaneous emission coefficients are those of
Allen (1973). Photoionization cross sections are from TOPBASE.
The
He III ion is represented by one level. With this He I-He II-He III system we treat in our computations 76 permitted
radiative transitions and 438 collisional transitions.


Up: Formation of helium spectrum
Copyright ESO 2001
![]() (Gouttebroze & Labrosse 2000).
(Gouttebroze & Labrosse 2000).
![]() and the first
excited level
and the first
excited level
![]() .
The latter is a metastable state and is the lower
state of the infrared He I
.
The latter is a metastable state and is the lower
state of the infrared He I ![]() 10830 Å line. In Fig. 2 we show some line transitions which will be the
subject of further investigations in Sects. 4 and 5, as well as the resonance continuum transition which
occurs at 504 Å. The optically thick resonance lines lie in the singlet
system. There are no permitted radiative transitions between the two systems,
but they are coupled through collisions. Effective collision strengths,
collisional ionization coefficients and spontaneous emission coefficients are
from BSS. Collisions strengths not defined in BSS
are taken in Benson & Kulander (1972). Coefficients for Stark broadening are from
Dimitrijevic & Sahal-Brechot (1984), and from Griem (1974) for transitions not defined in
Dimitrijevic & Sahal-Brechot. Photoionization cross sections are from TOPBASE
(Fernley et al. 1987).
10830 Å line. In Fig. 2 we show some line transitions which will be the
subject of further investigations in Sects. 4 and 5, as well as the resonance continuum transition which
occurs at 504 Å. The optically thick resonance lines lie in the singlet
system. There are no permitted radiative transitions between the two systems,
but they are coupled through collisions. Effective collision strengths,
collisional ionization coefficients and spontaneous emission coefficients are
from BSS. Collisions strengths not defined in BSS
are taken in Benson & Kulander (1972). Coefficients for Stark broadening are from
Dimitrijevic & Sahal-Brechot (1984), and from Griem (1974) for transitions not defined in
Dimitrijevic & Sahal-Brechot. Photoionization cross sections are from TOPBASE
(Fernley et al. 1987).