4 Free parameters

We will calculate the values of the relaxation time as a function of three free parameters, namely the number of field particles, the initial velocity of the test particles and the softening. In this section we will discuss what the relevant ranges for these parameters are.

   
4.1 Number of particles

We will consider numbers of particles between 1000 and 64000. Indeed fewer than 1000 particles are hardly used anymore in numerical simulations, even with direct summation. For more than 64000 particles the two-body relaxation is small. Furthermore the range considered is sufficiently large for all trends to be clearly seen.

   
4.2 Initial velocity

The question for the initial velocity is more convoluted. The simple analytical approaches leading to Eqs. (6) and (7), instead of taking a spectrum of velocities for the individual encounters and then integrating over these velocities, introduce an effective or average velocity and assume that all interactions are made at this velocity. In our numerical calculations individual encounters occur at different velocities, depending on their position on the trajectory of the test particle and on the initial velocity of this particle. We can, nevertheless, introduce $v_{\rm eff}$, an average or effective velocity, in a similar way as the analytical approximation. A simple and straightforward, albeit not unique, such definition can be obtained as follows: let us assume that the test particle moves on a straight line. At each point of its trajectory we can define a thin sheet going through this point and locally perpendicular to the trajectory. It will contain all field particles which have this point as their closest approach with the test particle. Let dr be the thickness of this sheet and $\lambda {\rm d}r$ the fraction of the total mass of the field particles that is in it. Then we can define the effective velocity

$$v_{\rm eff} = 2 \int_0^R \lambda v~ {\rm d}r,$$ (12)

which of course depends on both the distribution of the field particles and the initial velocity of the test particle.

   
4.3 Softening

Figure 2: MASE as a function of the softening $\epsilon$ for the three models described in this paper. The upper panel gives the results for model H, the middle one for model P, and the lower one for model D. In each panel from top to bottom the curves correspond to N = 1000, 2000, 4000, 8000, 16000, 32000 and 64000, where N is the number of particles in the realisation of each model. The number of realisations taken in all cases is $6 \times 10^6 / N$. The position of the minimum error along a line corresponding to a given N is marked by a $\times$, and the corresponding $\epsilon$value is the optimal softening $\epsilon _{\rm opt}$ for this number of particles.

The third free parameter in our calculations is the softening. Merritt (1996; hereafter M96) and Athanassoula et al. (2000; hereafter AFLB) showed that, for a given mass distribution and a given number of particles N, there is a value of the softening, called optimal softening $\epsilon _{\rm opt}$, which gives the most accurate representation of the gravitational forces within the N-body representation of the mass distribution. For values of the softening smaller than $\epsilon _{\rm opt}$ the error in the force calculation is mainly due to noise, because of the graininess of the configuration. For values of the softening larger than $\epsilon _{\rm opt}$ the error is mainly due to the biasing, since the force is heavily softened and therefore far from Newtonian. Since the two-body relaxation is also a result of graininess it makes sense to consider softening values for which it is the noise and not the bias that dominates, i.e. to concentrate our calculations mainly on values of the softening which are smaller than or of the order of $\epsilon _{\rm opt}$, keeping in mind that too small values of the softening have no practical significance. The value of the optimal softening decreases with N and can be well approximated by a power law

$$\begin{eqnarray*}\epsilon_{\rm opt}=BN^{b}, \end{eqnarray*}$$

(M96). The values of B and b depend on the mass distribution under consideration, and, to a much smaller degree, on the range of N considered (AFLB). Thus denser configurations require smaller softenings for an optimum representation of the force (AFLB). For a given number of particles the homogeneous and Plummer spheres have roughly the same optimal softening, while the Dehnen sphere with $\gamma=0$ has an optimal softening 0.45 dex lower (cf. Fig. 9 of AFLB).

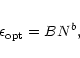
M96 and AFLB have calculated $\epsilon _{\rm opt}$ using the mean average square error (MASE) of the force, which measures how well the forces in an N-body representation of a given mass distribution represent the true forces in this distribution. The average square error (ASE) is defined as

$$ASE=\frac{\cal C}{N} \sum_{i=1}^{N}\vert F_i- F_{\rm true}(x_i)\vert^2,$$ (13)

where $F_{\rm true} (x_i)$ is the true force from a given mass distribution at a point x_i, F_i is the force calculated at the same position from a given N-body realisation of the mass distribution and using a given softening and method, N is the number of particles in the realisation, and the summation is carried out over all the particles. In order to get rid of the dependence on the particular configuration, which is of no physical significance, many realisations of the same smooth model must be generated and the results should be averaged over them. Thus MASE, the mean value of the ASE, is

$$MASE = \frac {\cal C} {N} <\sum_{i=1}^{N}\vert F_i- F_{\rm true}(x_i)\vert^2>$$ (14)

where <> indicates an average over many realisations. In Eqs. (13) and (14) ${\cal C}$ is a multiplicative constant, introduced to permit comparisons between different mass distributions. Since in this paper we are only interested in the values of $\epsilon _{\rm opt}$ we will simply use ${\cal C} = 1$. The MASE values were found using $6 \times 10^6 / N$ realisations and were calculated using direct summation on the Marseille GRAPE-5 systems.

Figure 2 shows values of MASE as a function of $\epsilon$ for the three models considered in Sects. 5.1 to 5.4 and seven values of N, in the range of values considered here (cf. Sect. 4.1). The general form of the curves is as expected. There is in all cases a minimum error between the region dominated by the noise (small values of the softening) and the region dominated by the bias (large values of the softening). This minimum - marked with a $\times$ in Fig. 2 - gives the value of $\epsilon _{\rm opt}$. For all three models a larger number of particles corresponds to a smaller error and a smaller value of $\epsilon _{\rm opt}$, as expected (M96, AFLB).

The more concentrated configurations give smaller values of $\epsilon _{\rm opt}$, as already discussed in AFLB. Thus for $N=64\,000$the optimum softening for model H is less than twice that of model P, while the ratio between the softenings of models P and D is more than 10.

Comparing our results to those of AFLB we can get insight on the effect of the truncation radius. For this it is best to compare our results obtained with $N = 32\,000$ with those given by AFLB for $N = 30\,000$, since these two N values are very close and we do not have to make corrections for particle number. For our model P and $N = 32\,000$ we find an optimum softening of 0.52, or, equivalently, 0.057$a_{\rm P}$, where $a_{\rm P}$ is the scale length of the Plummer sphere. This is smaller than the value of 0.063$a_{\rm P}$ found for the AFLB Plummer model and the difference is due to the different truncation radii of the two models. AFLB truncated their Plummer sphere at a radius of 38.71$a_{\rm P}$, which encloses 0.999 of the total mass of the untruncated sphere, while model P is truncated at 2.2$a_{\rm P}$, which contains only 75% of total mass. The difference in the values of $\epsilon _{\rm opt}$ is in good agreement with the discussion in Sect. 5.2 of AFLB. When the truncation radius is large, the model includes a relatively high fraction of low density regions, where the inter-particle distances are large. This is not the case if the truncation radius is much smaller, as it is here. Thus the mean inter-particle distance is larger in the former case and, as can be seen from Fig. 11 of AFLB, the corresponding optimal softening also. This predicts that the optimal softening should be smaller in models with smaller truncation radius, and it is indeed what we find here.

Our model H is the same as that of AFLB, except for the difference in the cut-off radii. Thus the values of the optimum softening are the same, after the appropriate rescaling with the cut-off radii has been applied. Our model D differs in two ways from the corresponding model of AFLB. We use here $\gamma=1$, while AFLB used $\gamma$= 0. We also truncated our model at 6.5$a_{\rm D}$, while AFLB truncated theirs at 2998$a_{\rm D}$. It is thus not possible to make any qualitative or quantitative comparisons.