5 Relaxation measured from angular deflections

   
5.1 The effect of the number of particles and of the density distribution

 

 

Table 1: Coefficients of linear regression in log-log scale of $T_{\rm relax}$ as a function of particle number N.

Model	$f_{\rm v}$	$\epsilon$	A1	B1	$\sigma_{A_1}$	$\sigma_{B_1}$
H			0.78	1.00	0.05	0.01
P	1.5	0.01	0.76	0.98	0.04	0.01
D			0.63	0.78	0.04	0.01
H			0.87	1.01	0.05	0.01
P	1.5	0.03	0.80	1.00	0.11	0.03
D			0.86	0.77	0.11	0.03
H			0.99	1.01	0.06	0.01
P	1.5	0.10	0.94	1.00	0.11	0.03
D			0.75	0.89	0.07	0.02
H			1.13	1.02	0.08	0.02
P	1.5	0.50	1.24	0.98	0.07	0.02
D			1.29	0.94	0.07	0.02
H			1.17	1.01	0.04	0.01
P	2.0	0.03	0.98	1.01	0.08	0.02
D			0.78	0.87	0.12	0.03
P	3.0	0.01	1.40	0.97	0.04	0.01

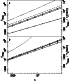Figure 3: Relaxation time as a function of the number of field particles, for $f_{\rm v}=1.5$ and three different mass models, namely model H (stars), model P ($\times$) and model D (crosses). The upper panel a) was obtained with $\epsilon =0.01$ and the lower b) with $\epsilon =0.5$. The straight solid lines are the corresponding linear least square fits. The dashed lines give the predictions of Eq. (7), when we use $b_{\rm max}=R$, while the dotted lines give the prediction of the corresponding equation obtained by using $b_{\rm max}=l$.

Figure 3 shows the relaxation time as a function of the number of particles for the models H, P and D described in the previous section. The upper panel was obtained for $f_{\rm v}=1.5$ and $\epsilon =0.01$ and the lower one for $f_{\rm v}=1.5$ and $\epsilon =0.5$. As can be seen from Fig. 2, for the first value of the softening noise dominates over bias for all three models. For the second value noise dominates for model H, bias dominates for model D, and we are near the optimum value for model P and the high N values. The left ordinate in Fig. 3 gives the relaxation time while the right one gives the ratio of the relaxation to transit time for the homogeneous sphere and $f_{\rm v}=1.5$. The corresponding values of this ratio for the other two density distributions can be easily obtained if one takes into account that for $f_{\rm v}=1.5$ the three theoretical transit times are 20.35, 17.52 and 16.91, for the H, P and D models respectively. We fitted straight lines

$$\begin{eqnarray*}\log_{10}(T_{\rm relax}) = A_1 + B_1 \log_{10}(N) \end{eqnarray*}$$

to each model using least-square fits and plotted them with solid lines in the figure. The values of A₁ and B₁, as well as of their corresponding uncertainties $\sigma_{A_1}$ and $\sigma_{B_1}$, are given in Table 1. We have performed similar calculations for other values of the velocity and softening parameters and have included in this Table the corresponding values of A₁ and B₁, as well as their uncertainties. From Fig. 3, other similar plots for other values of the softening and of the initial velocity (not presented here), and the values given in Table 1 we can reach a number of conclusions.

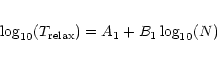
The dependence of $T_{\rm relax}$ on N is reasonably well represented by a straight line in the log-log plane and that for all values of the softening and $f_{\rm v}$ we tried and for all three models. The relaxation time for model D is always smaller than that for models P and H. The difference is much more important (${\sim} 1$ dex) for the smaller value of the softening, than for the larger one ( ${\sim} 0.15$ dex). Similarly, the relaxation time for Plummer distributions is somewhat smaller (${\sim}0.1$ dex) than that of the homogeneous one for small values of the softening, while for the larger value the two relaxation times do not differ significantly.

Figure 3 and Table 1 also show a trend for the slopes of the straight lines. For the small softening the homogeneous model has a relaxation time which is roughly proportional to the number of field particles in the configuration, and that is in good agreement with Eq. (7). This is not true any more for the more centrally concentrated mass distributions, which have a value of B₁less than unity. For model P the value of B₁ is slightly less than unity, but for model D it is considerably so. Thus when we increase the number of particles in the configuration, we increase the relaxation time relatively less in more centrally concentrated configurations than in less centrally concentrated ones. In other words not only is the relaxation time smaller in the more centrally concentrated configurations, but also it takes more particles to increase it by a given amount.

These trends for the slopes of the straight lines are also present for the larger value of the softening. The differences, however, between the slopes, i.e. between the corresponding values of B₁, are much smaller. Thus for $f_{\rm v}=1.5$ and $\epsilon =0.01$ there is a difference of roughly 25% between the slopes corresponding to models H and D, while this value is reduced to roughly 8% when $\epsilon =0.5$.

Figure 3 also compares the prediction of Eq. (7) with the results of our numerical calculations for the homogeneous sphere. The agreement is fairly good, particularly for the larger softening, where the difference is of the order of 0.08 dex. It should be noted that these predictions were obtained with $b_{\rm max}=R$, the cutoff radius of the system. A yet better agreement would have been possible if one used $b_{\rm max}=fR$, where f is a constant larger than 1. Since, however, this constant is a function of the softening used and perhaps also of the value of $f_{\rm v}$, it is not very useful to determine its numerical value. The results obtained by using $b_{\rm max}=l$, where l is the mean inter-particle distance, are given by open squares. We note that they give a bad approximation of the numerical results, particularly so for a large number of particles and for the value of the softening which is nearest to optimal. For the smaller softening the approximation with $b_{\rm max}=l$ is still considerably worse than that obtained with $b_{\rm max}=R$, but the difference is smaller than in the case of the optimal softening. Whether this will be reversed for an even smaller value of the softening or not is not possible to predict from the above calculations. Nevertheless, if it did happen, it would be for a value of the softening that gave a very bad representation of the forces within model H. Thus we can conclude that, at least for collisionless simulations which have a reasonable softening, the simple analytical estimates presented in Sect. 2 give a reasonable approximation of the relaxation time if we use $b_{\rm max}=R$, but not if we use $b_{\rm max}=l$. The latter gives too high a value of the relaxation time, and is therefore falsely reassuring.

We also compared our results with theoretical estimates using $\ln\Lambda=\ln(gN)$ for the Coulomb logarithm and different values of g, as tabulated by Giersz & Heggie (1994). We find that they always fare less well than Eq. (7) with $b_{\rm max}=R$, particularly for $\epsilon =0.01$. Amongst the values tried, g= 0.11, proposed by Giersz & Heggie (1994), gave the best fit for $\epsilon =0.5$, while the value g= 0.4(Spitzer 1987) was best for $\epsilon =0.01$. The differences between the results for various values of g are nevertheless small.

To summarise this section we can say that more centrally concentrated distributions have smaller relaxation times and that the difference is more important for smaller values of the softening. This argues that the relaxation time is more influenced by the maximum rather than by the average density.

   
5.2 The effect of velocity

Figure 4: Relaxation time as a function of the effective velocity of the test particles, for $N=64\,000$ and three different mass models, namely model H (stars), model P ($\times$) and model D (crosses). The straight lines are the corresponding linear least square fits. The upper panel corresponds to $\epsilon =0.01$ and the lower one to $\epsilon =0.5$.

  

 

Table 2: Coefficients of linear regression in log-log scale of $T_{\rm relax}$ as a function of $v_{\rm eff}$.

Model	$\epsilon$	A2	B2	$\sigma_{A_2}$	$\sigma_{B_2}$
H		4.84	2.72	0.02	0.04
P	0.01	4.58	2.39	0.02	0.04
D		2.33	4.28	0.20	0.35
H		5.20	2.83	0.01	0.02
P	0.5	5.02	2.53	0.02	0.04
D		4.42	2.90	0.06	0.11

In order to test the effect of velocity on the relaxation time we have launched test particles with different initial velocities.

Figure 4 shows the relaxation time as a function of the effective velocity of the particles, defined in Sect. 4, for the three density distributions under consideration. The calculations have been made with 64000 field particles and a softening of 0.01 for the upper panel and 0.5 for the lower one. The dependence is linear in the log-log plane for large values of the effective velocity and deviates strongly from it for small values. We thus fitted a straight line in the log-log plane to the higher velocities estimating for each of the mass models separately the number of points that could be reasonably fitted by a straight line. We give the constants of the regression

$$\begin{eqnarray*}\log_{10}(T_{\rm relax}) = A_2 + B_2 \log_{10} ({v_{\rm eff}}), \end{eqnarray*}$$

together with the corresponding error estimates, in Table 2.

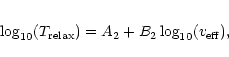
In all cases the relaxation time increases with the initial velocity of the particles. In order to compare this with the analytical predictions of Sect. 2 we note that the deviation of a particle from its trajectory due to an encounter should be smaller for larger impact velocities (cf. Eq. (2)), while larger impact velocities imply smaller crossing times. Thus from Eqs. (6) and (7) we note that $T_{\rm relax}$ should be proportional to the third power of the velocity, i.e. that the coefficient B₂ in Table 2 should be roughly equal to 3. We note that in the homogeneous case, which should be nearer to the analytical result, there is a difference of less than 10%, presumably due to the fact that the approximations of the analytical approach are too harsh. The differences with the results of models P and D are on average larger, but strictly speaking, Eqs. (6) and (7) do not apply to them.

   
5.3 The effect of softening

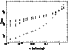Figure 5: Relaxation time as a function of the softening, for $N=64\,000$, $f_{\rm v}=1.5$ and three different mass models, namely model H (stars), model P ($\times$) and model D (crosses).

Figure 5 shows the relaxation time $T_{\rm relax}$ as a function of the softening $\epsilon$ for the case of $N=64\,000$ and $f_{\rm v}=1.5$. We note that the relaxation time increases with softening as expected. There is no simple linear dependence between the two plotted quantities. In fact the relaxation time increases much faster with $\log\epsilon$ for large values of the softening than for small ones. The point at which this change of slope occurs is roughly the same for models H and P, and much smaller for model D. In fact in all cases it is roughly at the position of the corresponding optimal softening, which is roughly the same for models H and P and considerably smaller for model D (cf. Sect. 4.3). Thus the change of slope must correspond to a change between a noise dominated regime and a bias dominated one.

In the noise dominated regime the sequence between the three models is the same as in previous cases. Namely it is model H that has the largest relaxation time, followed very closely by model P, and less closely by model D. It is interesting to note that for high values of the softening the three curves intersect. Such values, however, are too dominated by bias to be relevant to N-body simulations.

Figure 5 shows the only examples in this paper in which the error bars are large enough to be plotted, i.e. for which $\sigma_{T_{\rm relax}}/T_{\rm relax} > 0.05$. These occur for the smallest values of the softening, used here more for reasons of completeness than for their practical significance.

   
5.4 GRAPE-3 results compared to GRAPE-4 results

All results presented so far were made on one of the Marseille GRAPE-3 systems (Athanassoula et al. 1998). Such systems, however, are known to have limited accuracy, since they use 14 bits for the masses, 20 bits for the positions and 56 bits for the forces. One could thus worry whether this would introduce any extra graininess, which in turn would decrease the relaxation time.

 

 

Table 3: Relaxation time $T_{\rm relax}$ of model D with $f_{\rm v}=1.5$ and $\epsilon =0.01$, obtained by the GRAPE-3 (G3) and GRAPE-4 (G4) machines.

N	G3	G4	$\Vert$G3-G4$\Vert$/G4
1000	1040	1007	0.0328
2000	1626	1633	0.0043
4000	2698	2707	0.0033
8000	4834	4845	0.0023
16000	8143	8123	0.0025
32000	14490	14548	0.0040
64000	25858	25860	0.0001

In order to test this we repeated on GRAPE-4, which is a high accuracy machine, some of the calculations made also with GRAPE-3. For this purpose, we ran 7 configurations of model D with $f_{\rm v}=1.5$, $\epsilon =0.01$ and different number of field particles. The calculated relaxation time, $T_{\rm relax}$, obtained by the GRAPE-3 and GRAPE-4 runs, together with their differences, are shown in Table 3. As we can see the results have, in all but one case, a difference less than 0.5%. Only in the case of N=1000 does the difference rise to 3%, but as we mentioned before, this very low number of particles is hardly used nowadays, even in direct summation simulations on a general purpose computer.

   
5.5 Predicting the value of T $\mathsf{_{relax}}$ for an N-body simulation

In the standard version of the angular deflection method we have used so far all the test particles start from the same radius with the same initial velocity. On the other hand in any N-body realisation of a given model the particles have different apocenters. It is thus necessary to extend this method somewhat in order to obtain an estimate of how long a given N-body simulation will remain unaffected by two-body relaxation. Let us consider a simple model consisting of a Plummer sphere of total mass 20 and scale length 9.2, truncated at a radius equal to 30.125, i.e. at a radius containing roughly 7/8 of the total mass. As an example we wish to estimate the relaxation time of a 74668-body realisation of this model which will be evolved with a softening of 0.5, a value near the optimal softening for model P. For this we will somewhat modify the standard angular deflection method in order to consider several groups, starting each at a given radius. We first calculate the relaxation time from each group separately. The relaxation time of the model will be a weighted average of the relaxation times of the individual groups. The weights have to be calculated in such a way that the mean velocities with which the test particles encounter the field particles at any given radius represent fairly well the encounter velocities between any two particles in the N-body realisation, which is not far from the dispersion of velocities. We found we could achieve this reasonably well by considering 18 groups, of 10000 test particles each, with apocenters $R_{\rm max} (i) = 1.25 i + 2.5;\, i = 1,..18$. Each group starts from a distance such that $f_{\rm v} = 0.2$ and we weight the results of each by 3^-i, i = 1,..18. These weighting factors were just found empirically after a few trials and deemed adequate since they give an approximation of the velocity dispersion of the Plummer sphere of the order of 10 per cent. It would of course be possible to get a better representation by using a larger number of groups and e.g. some linear programming technique, but since we only need to have a rough approximation of the encounter velocities and the fit we obtained is adequate, we did not deem it necessary to complicate the problem unnecessarily.

As expected, we find that the relaxation time and the transit time are larger for groups with larger initial radius. The range of values we find is rather large. Thus for the innermost group we find a relaxation time of $1.6 \times 10^4$ and a transit time of 4, while for the outermost group the corresponding values are $3.6 \times 10^5$and 51. The weighted average of the relaxation time, taken over all orbits in the representation, is $3.4 \times 10^4$, and that of the transit time 4.9, i.e. nearer to those of the inner groups due to their larger weights.

A comparison with the estimates of the simple analytical formula given in Eq. (7) is not straightforward, since one has to adopt a characteristic radius, and the result is heavily dependent on that. Thus if we adopt an outer radius, where the virial velocity is small and therefore the crossing time large, we obtain very large values of the relaxation time, like those we find for the outer parts of our model Plummer sphere. On the other hand if we take the half mass radius then we obtain $T_{\rm relax}=3.1 \times 10^4$, in good agreement with our estimate obtained from the weighted average of all groups.

Our model P is sufficiently similar to the $W_{\rm c} = 5$ King model used by Huang et al. (1993) to allow comparisons. These authors obtain the relaxation time by monitoring the change of energy of individual particles in a simulation. They consider only particles which at the end of the simulation are near the half mass radius and find a relaxation time which, rescaled to our units, is $2.5 \times 10^5$. Thus this estimate is based on a group of particles which have their apocenters at or beyond the half mass radius. Applying our own method only to such particles also we obtain a relaxation time of $2.3 \times 10^5$, which is in excellent agreement with the value of Huang et al. (1993).